
- •44. Деформации при кручении. Расчет на жесткость
- •45. Энергия упругой деформации
- •46. Статически неопределимые задачи при кручении
- •47.Кручение стержня прямоугольного сечения
- •48. Изгиб. Определение. Виды изгиба
- •49. Внутренние силы при изгибе. Определение. Правило знаков при построении эпюр
- •50. Дифференциальные зависимости при изгибе
- •51. Контроль правильности построения эпюр
- •52. Определение внутренних усилий через напряжения при изгибе
- •53. Определение нормальных напряжений при изгибе
- •54. Положение нейтральной оси при изгибе
- •55. Осевой момент сопротивления. Эпюра распределения нормальных напряжений в поперечном сечении при изгибе. Условие прочности по нормальным напряжениям
- •56. Определение касательных напряжений при изгибе
- •57. Эпюра распределения касательных напряжений в поперечном сечении при изгибе. Условие прочности по касательным напряжениям
- •62. Энергия упругой деформации при изгибе
- •63. Напряженное состояние в точке. Главные площадки и напряжения. Виды напряженных состояний.
54. Положение нейтральной оси при изгибе
Рассмотрим
загруженную балку. В поперечном сечении
выделим элементарный уч-ток
 ,
по кот. действует усилие
,
по кот. действует усилие
 .
БЫЛ РИСУНОК 1 Выберем
сис-му координат: x
– нейтральная ось,y
– силовая ось,z
– продольная ось. Т.к. элемент испытывает
чистый сгиб ( нет растяжения), то продольная
сила равна нулю.
.
БЫЛ РИСУНОК 1 Выберем
сис-му координат: x
– нейтральная ось,y
– силовая ось,z
– продольная ось. Т.к. элемент испытывает
чистый сгиб ( нет растяжения), то продольная
сила равна нулю.
 ,
,
 Подставляем сюда выражение
(1):
Подставляем сюда выражение
(1):
 т.к.
т.к.
 ,
то
,
то
 Известно, что статический момент относ.
нейтральной оси равен 0
Известно, что статический момент относ.
нейтральной оси равен 0
 нейтральн. ось x
проходит через центр тяжести сечения.
Т.к. изгиб относительно оси y
отсутствует, то
нейтральн. ось x
проходит через центр тяжести сечения.
Т.к. изгиб относительно оси y
отсутствует, то
 ,
подстав. выр-ние (1):
,
подстав. выр-ние (1):
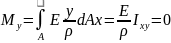 ,
т.к.
,
то
,
т.к.
,
то
 Известно, что центробежный момент
инерции
Известно, что центробежный момент
инерции
 относит. главных осей =0
относит. главных осей =0
 оси
x
и y
являются главными центральными.
оси
x
и y
являются главными центральными.
55. Осевой момент сопротивления. Эпюра распределения нормальных напряжений в поперечном сечении при изгибе. Условие прочности по нормальным напряжениям
Из
ф-лы
 видно: если
видно: если
 ,
, =0;
если
=0;
если
 ,
то
,
то
 Т.о. эпюра распределения нормальных
напряжений по высоте сечения имеет вид:
БЫЛ РИСУНОК 1 чем
больше
,
тем больше напряжение
.
Вывод: Нормальное напряжение в сечении
распределяется по линейному закону. На
нейтральной оси норм. напряжение =0. В
точках наиболее удаленных от нейтральной
оси напряж. максимально. Представим
ф-лу
в др. виде:
Т.о. эпюра распределения нормальных
напряжений по высоте сечения имеет вид:
БЫЛ РИСУНОК 1 чем
больше
,
тем больше напряжение
.
Вывод: Нормальное напряжение в сечении
распределяется по линейному закону. На
нейтральной оси норм. напряжение =0. В
точках наиболее удаленных от нейтральной
оси напряж. максимально. Представим
ф-лу
в др. виде:
 - осевой момент сопротивления – это
отношение осевого момента инерции к
расстоянию от нейтральной оси до наиболее
удаленной точки в сечении. Найдем момент
сопротивления для некоторых сечений:
1) прямоугольное сечение: БЫЛ
РИСУНОК 2
- осевой момент сопротивления – это
отношение осевого момента инерции к
расстоянию от нейтральной оси до наиболее
удаленной точки в сечении. Найдем момент
сопротивления для некоторых сечений:
1) прямоугольное сечение: БЫЛ
РИСУНОК 2
 2) для круглого сечения: БЫЛ
РИСУНОК 3
2) для круглого сечения: БЫЛ
РИСУНОК 3
 3) с вырезанным сечением: БЫЛ
РИСУНОК 4
3) с вырезанным сечением: БЫЛ
РИСУНОК 4
 . Зная моменты сопротивления
можно записать условие прочности по
норм. напряжениям: для симметрич. сечений
относ. нетральной оси
. Зная моменты сопротивления
можно записать условие прочности по
норм. напряжениям: для симметрич. сечений
относ. нетральной оси
 .
Рассмотрим несимметричное сечение:
БЫЛ РИСУНОК 5
.
Рассмотрим несимметричное сечение:
БЫЛ РИСУНОК 5
 .
Если материал неодинаково сопротивляется
расяж. сжат., то записываем два условия
прочности, отдельно для сжатой и
растянутой областей
.
Если материал неодинаково сопротивляется
расяж. сжат., то записываем два условия
прочности, отдельно для сжатой и
растянутой областей
 ;
;

56. Определение касательных напряжений при изгибе
При
поперечном изгибе в поперечных и
продольных сечениях балки возникают
касательные напряжения.
БЫЛ РИСУНОК 1 В основу
теории касательных напряжений положено
2 гипотезы: 1) касательное напряжение
действует параллельно оси у; 2) в местах
одинаково удаленных от нейтральной оси
касательное напряжение одинаково. Для
определ. касательного напряж. рассмотрим
загруженную балку прямоугольного
сечения. Двумя сечениями вырежем
элементарный уч-ток
и шириной
 равной ширине балки. БЫЛ
РИСУНОК 2 Покажем
распределение нормальных и касательных
напряжений по сечениям 1-1 и 2-2. На некотором
расстоянии от нейтрального слоя сделаем
продольное сечение m-n.
В этом сечении действует касательное
напряжение. Покажем равнодействующие
действующие на заштрихованную часть:
нормальных сил
равной ширине балки. БЫЛ
РИСУНОК 2 Покажем
распределение нормальных и касательных
напряжений по сечениям 1-1 и 2-2. На некотором
расстоянии от нейтрального слоя сделаем
продольное сечение m-n.
В этом сечении действует касательное
напряжение. Покажем равнодействующие
действующие на заштрихованную часть:
нормальных сил
 ;
касательных сил. Как известно напряжение
в любой точке на расстоянии у определяется
по ф-ле:
.
Найдем равнодействующую:
;
касательных сил. Как известно напряжение
в любой точке на расстоянии у определяется
по ф-ле:
.
Найдем равнодействующую:
 ;
;
 ;
;
 где
где
 – площадь элементарного слоя на ур-не
сечения m-n.
Запишем условие равновесия:
– площадь элементарного слоя на ур-не
сечения m-n.
Запишем условие равновесия:
 ;
;
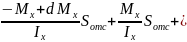
 .
Для нахождения касат. напряж. в этом
сечении запишем:
.
Для нахождения касат. напряж. в этом
сечении запишем:
 ;
;
 .
Ф-ла Журавского для оред. касат. напряж.
в любой точке поперечного сечения балки:
.
Ф-ла Журавского для оред. касат. напряж.
в любой точке поперечного сечения балки:

