
- •44. Деформации при кручении. Расчет на жесткость
- •45. Энергия упругой деформации
- •46. Статически неопределимые задачи при кручении
- •47.Кручение стержня прямоугольного сечения
- •48. Изгиб. Определение. Виды изгиба
- •49. Внутренние силы при изгибе. Определение. Правило знаков при построении эпюр
- •50. Дифференциальные зависимости при изгибе
- •51. Контроль правильности построения эпюр
- •52. Определение внутренних усилий через напряжения при изгибе
- •53. Определение нормальных напряжений при изгибе
- •54. Положение нейтральной оси при изгибе
- •55. Осевой момент сопротивления. Эпюра распределения нормальных напряжений в поперечном сечении при изгибе. Условие прочности по нормальным напряжениям
- •56. Определение касательных напряжений при изгибе
- •57. Эпюра распределения касательных напряжений в поперечном сечении при изгибе. Условие прочности по касательным напряжениям
- •62. Энергия упругой деформации при изгибе
- •63. Напряженное состояние в точке. Главные площадки и напряжения. Виды напряженных состояний.
49. Внутренние силы при изгибе. Определение. Правило знаков при построении эпюр
При
изгибе в поперечном сечении возникают
внутренние силы, кот. определяются
методом сечений. БЫЛ
РИСУНОК 1
 Мысленно брус рассекаем и рассматриваем
равновесие правой части. Для ее равновесия
в сечении будут действовать поперечная
сила и изгибающий момент.
БЫЛ РИСУНОК 2
Мысленно брус рассекаем и рассматриваем
равновесие правой части. Для ее равновесия
в сечении будут действовать поперечная
сила и изгибающий момент.
БЫЛ РИСУНОК 2
 .
Поперечная сила
.
Поперечная сила
 в любом сечении численно равна
алгебраической сумме проекции на пл-сть
сечения всех внешних сил, действ. по
одну сторону от сечения. Изгибающий
момент
в сечении численно равен алгебраической
сумме моментов внешних сил, действующ.
по одну сторону от сечения относительно
центра тяжести сечения. Правило знаков:
Если внешние силы вращают балку
относительно сечения по часовой стрелки,
то поперечные силы
больше нуля, если против –меньше нуля.
БЫЛ РИСУНОК 3 БЫЛ РИСУНОК 4 Если
внешняя сила или момент стремятся
изогнуть балку относительно сечения
вверх, то изгибающий момент
в любом сечении численно равна
алгебраической сумме проекции на пл-сть
сечения всех внешних сил, действ. по
одну сторону от сечения. Изгибающий
момент
в сечении численно равен алгебраической
сумме моментов внешних сил, действующ.
по одну сторону от сечения относительно
центра тяжести сечения. Правило знаков:
Если внешние силы вращают балку
относительно сечения по часовой стрелки,
то поперечные силы
больше нуля, если против –меньше нуля.
БЫЛ РИСУНОК 3 БЫЛ РИСУНОК 4 Если
внешняя сила или момент стремятся
изогнуть балку относительно сечения
вверх, то изгибающий момент
 больше нуля, если вниз – меньше нуля.
БЫЛ РИСУНОК 5 БЫЛ РИСУНОК 6
больше нуля, если вниз – меньше нуля.
БЫЛ РИСУНОК 5 БЫЛ РИСУНОК 6
50. Дифференциальные зависимости при изгибе
Установим
зависимость между поперечной силой
,
изгибающим моментом
и интенсидностью распределенной нагрузки
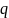 .
БЫЛ РИСУНОК 1 Поперечная
сила
и изгибающий момент
.
БЫЛ РИСУНОК 2
.
БЫЛ РИСУНОК 1 Поперечная
сила
и изгибающий момент
.
БЫЛ РИСУНОК 2
 – приращение величин внутренних сил.
Составим ур-ние статики: 1.
– приращение величин внутренних сил.
Составим ур-ние статики: 1.
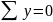 ,
,
 ;
;
 ;
;
 - первая производная от поперечной силы
по длине равна интенсивности распределенной
нагрузки. 2.
- первая производная от поперечной силы
по длине равна интенсивности распределенной
нагрузки. 2.
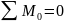 ,
,
 ;
;
 ;
;
 – первая производная от изгибающего
момента по длине равна поперечной силе.
Теорема Журавского:
– первая производная от изгибающего
момента по длине равна поперечной силе.
Теорема Журавского:

51. Контроль правильности построения эпюр
БЫЛ
РИСУНОК 1 Диф-ые
зависимость использ. для контроля
правильности построения эпюр: 1) на
уч-ке, где
 поперечная сила
постоянна (
поперечная сила
постоянна ( );
);
 ;
;
 БЫЛ РИСУНОК 2 а
изгибающий момент изменяется по линейному
закону
;
БЫЛ РИСУНОК 2 а
изгибающий момент изменяется по линейному
закону
;
 2)на уч-ке, где распределенная нагрузка
постоянна
2)на уч-ке, где распределенная нагрузка
постоянна ;
;
 .
Поперечная сила изменяется по линейному
закону, а изгибающий момент по
параболическому:
.
Поперечная сила изменяется по линейному
закону, а изгибающий момент по
параболическому:
 ;
;
 ;
3) В местах приложения сосредоточенной
силы на эпюре
имеется скачок на величину этой силы.
4) В местах приложения сосредоточенного
момента на эпюре
имеется скачок, равный величине момента;
на эпюре
никаких изменений. 5) В местах перехода
поперечной силы через ноль изгибающий
момент принимает экстремальное значение.
;
3) В местах приложения сосредоточенной
силы на эпюре
имеется скачок на величину этой силы.
4) В местах приложения сосредоточенного
момента на эпюре
имеется скачок, равный величине момента;
на эпюре
никаких изменений. 5) В местах перехода
поперечной силы через ноль изгибающий
момент принимает экстремальное значение.
52. Определение внутренних усилий через напряжения при изгибе
При плоском
поперечном изгибе в каждой точке
поперечного сечения будет возникать
нормальное и касательное напряжение.
Установим связь между внутренними
усилиями и напряжением. БЫЛ
РИСУНОК 1 БЫЛ РИСУНОК 2 Поперечной
силой
 наз. равнодействующая всех внутренних
касательных сил, действующих в поперечном
сечении. Изгибающим моментом
наз. равнодействующая всех внутренних
касательных сил, действующих в поперечном
сечении. Изгибающим моментом
 наз. результирующий момент всех внутренних
нормальных сил, действующ. в поперечном
сечении.
наз. результирующий момент всех внутренних
нормальных сил, действующ. в поперечном
сечении.
53. Определение нормальных напряжений при изгибе
Рассмотрим
случай чистого изгиба, когда в поперечном
сечении балки возникает только изгибающий
момент. БЫЛ РИСУНОК 1
Проведем опыт. На пов-ть
балки нанесем ряд параллельных продольных
и поперечных линий. БЫЛ
РИСУНОК 2 БЫЛ
РИСУНОК 3 Наблюдения
показали, что продольные линии изогнулись,
причем часть из них удлинилась , часть
укоротилась, продольная ось z
не изменила своей длины, поперечные
линии остались прямыми, но повернулись
на некоторый угол. Из этого следует: 1)
продольные волокна испытывают простое
растяжение сжатие. Существует слой
балки, который не деформируется, наз.
нейтральным слоем. 2) гипотеза плоских
сечений подтверждается. Плоские
поперечные сечения остаются плоскими
до деформации и после. 3)при чистом изгибе
в сечении отсутствует касательное
напряжение, т.е. нет сдвига, т.к. углы
сетки остались прямыми. На основе этих
гипотез выводится ф-ла:……..Выделим
из рассматриваемой балки элементарный
участок длиной
 БЫЛ РИСУНОК 4 на
расстоянии у от нейтрального слоя
выделим элементарный участок длиной
БЫЛ РИСУНОК 4 на
расстоянии у от нейтрального слоя
выделим элементарный участок длиной
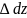 .
.
 - радиус кривизны нейтрального слоя;
- радиус кривизны нейтрального слоя;
 – усилие по элементарной площадке.
Первонач. длина на ур-не нейтрального
слоя
– усилие по элементарной площадке.
Первонач. длина на ур-не нейтрального
слоя
 .
Абсолютное удлинение рассматриваемого
уч-ка равно:
.
Абсолютное удлинение рассматриваемого
уч-ка равно:
 .
Относительное удлинение:
.
Относительное удлинение:
 Т.к. продольные волокна испытывают
простое растяжение сжатие, то используя
закон Гука получим:
Т.к. продольные волокна испытывают
простое растяжение сжатие, то используя
закон Гука получим:
 (1) Найдем момент внутренних сил
относительно нейтральных осей:
(1) Найдем момент внутренних сил
относительно нейтральных осей:
 Из этой ф-лы определим кривизну
нейтрального слоя:
Из этой ф-лы определим кривизну
нейтрального слоя:
 Подставляем значение кривизны в ф-лу
(1) и получим:
Подставляем значение кривизны в ф-лу
(1) и получим:
 .
Ф-ла для определения нормального
напряжения в любой точке поперечного
сечения балки, где
.
Ф-ла для определения нормального
напряжения в любой точке поперечного
сечения балки, где
 - изгибающий момент в рассматриваемом
сечении балки;
- изгибающий момент в рассматриваемом
сечении балки;
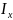 - осевой момент инерции сечения
относительно нейтральной оси;
- осевой момент инерции сечения
относительно нейтральной оси;
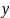 - расстояние от исследуемой точки до
нейтральной оси.
- расстояние от исследуемой точки до
нейтральной оси.
