
- •44. Деформации при кручении. Расчет на жесткость
- •45. Энергия упругой деформации
- •46. Статически неопределимые задачи при кручении
- •47.Кручение стержня прямоугольного сечения
- •48. Изгиб. Определение. Виды изгиба
- •49. Внутренние силы при изгибе. Определение. Правило знаков при построении эпюр
- •50. Дифференциальные зависимости при изгибе
- •51. Контроль правильности построения эпюр
- •52. Определение внутренних усилий через напряжения при изгибе
- •53. Определение нормальных напряжений при изгибе
- •54. Положение нейтральной оси при изгибе
- •55. Осевой момент сопротивления. Эпюра распределения нормальных напряжений в поперечном сечении при изгибе. Условие прочности по нормальным напряжениям
- •56. Определение касательных напряжений при изгибе
- •57. Эпюра распределения касательных напряжений в поперечном сечении при изгибе. Условие прочности по касательным напряжениям
- •62. Энергия упругой деформации при изгибе
- •63. Напряженное состояние в точке. Главные площадки и напряжения. Виды напряженных состояний.
44. Деформации при кручении. Расчет на жесткость
При кручении
бруса сечения поворачиваются друг
относительно друга на угол
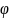 называемый углом закручивания. При
выводе ф-лы касательных напряжений была
установлена зависимость:
называемый углом закручивания. При
выводе ф-лы касательных напряжений была
установлена зависимость:
 Угол закручивания по длине l
будет равен:
Угол закручивания по длине l
будет равен:
 , где произведение
, где произведение
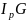 - жесткость при кручении. Если на каком-то
участке
- жесткость при кручении. Если на каком-то
участке
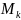 ,
- постоянны, то угол закручивания на
уч-ке определяется:
,
- постоянны, то угол закручивания на
уч-ке определяется:
 .
Зная допускаемый угол закручивания на
определенной длине можно записать
условие жесткости:
.
Зная допускаемый угол закручивания на
определенной длине можно записать
условие жесткости: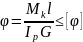 .
Угол закручивания является абсолютной
деформацией при кручении. Угол
закручивания, приходящийся на единицу
длины, наз. относительным углом
закручивания, обознач.
.
Угол закручивания является абсолютной
деформацией при кручении. Угол
закручивания, приходящийся на единицу
длины, наз. относительным углом
закручивания, обознач.
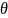 :
:
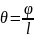 .
Тогда условие жесткости можно записать
в другом виде:
.
Тогда условие жесткости можно записать
в другом виде:
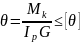 .
.
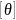 - допускаемый относительный угол
закручивания.
- допускаемый относительный угол
закручивания.
45. Энергия упругой деформации
Если подвергнуть
действию крутящего момента стержень,
то известно, что в упругой стадии
зависимость между скручивающим моментом
и углом закручивания линейная. БЫЛ
РИСУНОК В этом случае
работа внешних сил затрачиваемая на
кручение вала будет равна кол-ву
потенциальной энергии накопленной в
вале:
 .
Работа равна площади заштрихованного
треугольника на диаграмме кручения,
тогда:
.
Работа равна площади заштрихованного
треугольника на диаграмме кручения,
тогда:
 ,
учитывая
,
учитывая
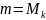 ,
.
Полная энергия упругой деформации для
уч-ка вала с постоянной жесткостью:
,
.
Полная энергия упругой деформации для
уч-ка вала с постоянной жесткостью:

46. Статически неопределимые задачи при кручении
Иногда
можно встретить стержни работающие на
кручение, кот. невозможно рассчитать,
используя только ур-ние статики.
Рассмотрим загруженный вал, защемленный
с двух концов. БЫЛ РИСУНОК
1 В опорах возникнут
опорные моменты
 .
Составим ур-ние равновесия: 1.
.
Составим ур-ние равновесия: 1.
 =0
В этом ур-нии два неизвестных момента
=0
В этом ур-нии два неизвестных момента
 сис-ма
1 раз статически неопределима. Поэтому
необходимо составить дополнительное
ур-ние, рассмотрев деформацию сис-мы.
Отбрасываем правую часть: БЫЛ
РИСУНОК 2 Ур-ние деформации
составляем из условия, что угол
закручивания опоры В
равен нулю
сис-ма
1 раз статически неопределима. Поэтому
необходимо составить дополнительное
ур-ние, рассмотрев деформацию сис-мы.
Отбрасываем правую часть: БЫЛ
РИСУНОК 2 Ур-ние деформации
составляем из условия, что угол
закручивания опоры В
равен нулю
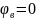 .
2.
.
2.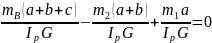 .
Решая совместно ур-е статики и ур-ние
деформации определим неизвестные
опорные моменты. В дальнейшем расчет
ведется как для статически определимой
сис-мы.
.
Решая совместно ур-е статики и ур-ние
деформации определим неизвестные
опорные моменты. В дальнейшем расчет
ведется как для статически определимой
сис-мы.
47.Кручение стержня прямоугольного сечения
БЫЛ
РИСУНОК 1 При кручении
стрержня прямоугольного сечения гипотеза
плоских сечений не выполняется, сечения
искривляются или деформируются. В
поперечных сечениях возникают касательные
напряжения, кот. возможно определить
только методами теории упругости. Эпюра
распределения
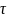 в поперечном сечении имеет вид: БЫЛ
РИСУНОК 2 Из эпюры видно
в центре тяжести и в угловых точках
касательное напряжение равно нулю. В
т.1 и т.2 касательное напряжение максимально
и определяется по ф-ле:
в поперечном сечении имеет вид: БЫЛ
РИСУНОК 2 Из эпюры видно
в центре тяжести и в угловых точках
касательное напряжение равно нулю. В
т.1 и т.2 касательное напряжение максимально
и определяется по ф-ле:
 ;
где
;
где
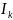 – приведенный момент инерции;
– приведенный момент инерции;
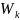 - приведенный момент сопротивления.
- приведенный момент сопротивления.
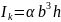 ;
;
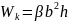 где
где
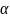 и
и
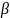 - коэффициенты, зависящие от соотношения
длин сторон прямоугольника.
- коэффициенты, зависящие от соотношения
длин сторон прямоугольника.
48. Изгиб. Определение. Виды изгиба
В
практике чаще всего встречаются
конструкции или их элементы, кот.
подвергаются действию поперечных
нагрузок. Под действием таких сил
стержень изгибается и называется балкой.
При изгибе балки в ее поперечных сечениях
могут возникать две внутренние силы:
поперечная сила Q
и изгибающий момент
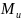 .
Такой изгиб наз. поперечным. Если в
поперечных сечениях возникает только
изгибающий момент, то изгиб наз. чистым.
Если плоскость действия сил совпадает
с одной из главных плоскостей, то изгиб
наз. плоским. Если силовая плоскость
не совпадает с главной плоскостью, то
изгиб наз. косым. Главная пл-сть совпадает
с пл-стью симметрии сечения. БЫЛ
РИСУНОК 1 БЫЛ
РИСУНОК 2
.
Такой изгиб наз. поперечным. Если в
поперечных сечениях возникает только
изгибающий момент, то изгиб наз. чистым.
Если плоскость действия сил совпадает
с одной из главных плоскостей, то изгиб
наз. плоским. Если силовая плоскость
не совпадает с главной плоскостью, то
изгиб наз. косым. Главная пл-сть совпадает
с пл-стью симметрии сечения. БЫЛ
РИСУНОК 1 БЫЛ
РИСУНОК 2
