3.3Тест програми.
Виконаємо тест програми у
полі введення даних введемо величини
елементів наприклад:
=100
Ом,
=30
Ом, С = 0,001
Ф, L = 3,8 Гн,
Е = 100 В, крайні точки графіків залишимо
рівними тим значенням яким вони
дорівнювали при старті програми.
Правильне введення даних зображено на
рисунку . Після введення даних ми
натискаємо кнопку початок розрахунку.
Рисунок
– Правильне введення даних;
На рисунку ми бачимо програму після правильного введення даних і початку розрахунку.
Рисунок
– програма з правильними даними після
початку розрахунку;
Програма виконає необхідні розрахунки і виведе графіки перехідних процесів на елементах. У полі керування графіками залишається тільки вибрати елемент на якому потрібно вивести графік перехідного процесу. Графік струму першої гілки зображено на рисунку . Графік струму другої гілки зображено на рисунку . Графік струму третьої гілки зображено на рисунку . Графік напруги на конденсаторі зображено на рисунку . Графік напруги на першому опорі зображено на рисунку . Графік напруги на другому опорі зображено на рисунку . Графік напруги на котушці зображено на рисунку .
Рисунок
– Струм першої гілки
;
Рисунок
– Струм другої гілки
;
Рисунок
– Струм третьої гілки
;
Рисунок
– Напруга на конденсаторі C;
Рисунок
– Напруга на котушці L;
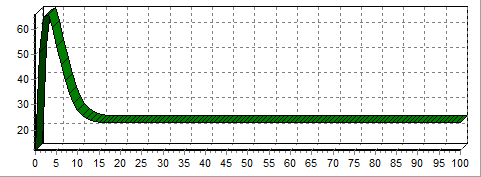Рисунок
– Напруга на першому опорі
;
Рисунок – Напруга на другому опорі ;
Якщо ж дані ввести невірно то програма виведе помилку при введенні даних. Дані потрібно буде ввести знову але правильно і натиснути кнопку почати розрахунок. Повідомлення про помилку буде виглядати так, як зображено на рисунку .
Рисунок
– Неправильне введення даних;
Висновок
Цей курсовий проект був виконаний в повній відповідності поставленому завданню і відлагоджений в серодовищі Delphi 7.0. В ході виконання курсової роботи була розроблена програма для розрахунку перехідних процесів для заданої схеми.
В результаті даної курсової роботи, я переконався в широких можливостях мови програмування Object Pascal і середовища проектування Delphi 7. Ознайомився з деякими новими функціями для реалізації графічного інтерфейсу, щоб зробити його більш зручним для користувача. При графічній реалізації проекту мною були використані функції, з якими легко працювати операторові, що зробило інтерфейс програми дуже зручним.
Я вважаю що в повній мірі впорався з поставленим переді мною завданням і програма повністю виконує функції, що від неї вимагаються.
Використана література
Галиссев Г.В. Програмирование в среде Delphi 7: Самоучитель. – М.: Диалектика, 2003. – 286 с.
Культин Н. Delphi 6. Програмирование на Object Pascal. СПб: БХВ – Петербург, 2001. – 528 с.
Рибалко М.П. Теоретичні основи електротехніки: Лінійні електричні кола: Підручник. Донецьк: Новий світ, 2003. – 513 с.
Додаток а. Виведення формул
Розглянемо приклади розрахунку повних перехідних струмів і напруг для трьох варіантів коренів характеристичного рівняння:
1)корені дійсні однакові;
2) корені дійсні різні;
3) корені комплексні;
1)Корені характеристичного рівняння дійсні однакові. Конденсатор був попередньо заряджений до напруги –Е В.
Розрахунок напруги на конденсаторі:
Представимо напругу на конденсаторі як суму примушеної й вільної складових:
, ()
де
–
напруга на конденсаторі;
–
примушена складова напруги;
–
вільна складова напруги;
Після замикання ключа в сталому режимі
струм
,
струми
та
рівні один одному й напруга на конденсаторі
дорівнює напрузі на другому резисторі:
, ()
де
–
примушена складова напруги;
– величина другого опору;
– величина другого опору;
–
значення джерела ЕРС;
Для визначення характеристичного рівняння складемо розрахункову схему як зображено на рисунку A.1.
Рисунок
(A.1)
– Розрахункова схема;
Визначимо формулу характеристичного опору Z(p) і дорівняємо його до нуля:
, ()
де Z(p)
– характеристичний опір;
– змінна яку потрібно знайти;
– ємність конденсатора;
– величина другого опору;
– величина другого опору;
– індуктивність котушки;
Виведене рівняння зведемо до квадратного:
, ()
Вираховуємо значення дискримінанту за формулою:
, ()
де 
– дискримінант квадратного рівняння;
– змінна яку потрібно знайти;
– ємність конденсатора;
– величина другого опору;
– величина другого опору;
– індуктивність котушки;
Оскільки дискримінант дорівнює нулю то корні мають однакове значення і розраховуються за формулою:
, ()
де 
– корні характеристичного рівняння;
– ємність конденсатора;
– величина другого опору;
– величина другого опору;
– індуктивність котушки;
Далі ми повинні знайти значення
постійних інтегрування
та
.
Туму що значення вільної складової
напруги на конденсаторі ми представляємо
у вигляді:
, ()
де 
–
вільна складова напруги на конденсаторі;
,
–
постійні інтегрування;
– корні характеристичного рівняння;
–
час проходження перехідного
процесу;
Для визначення цих значень ми складаємо систему рівнянь для початкових умов до комутації:
()
,
Запишемо ці рівняння для початкового моменту часу t=0 і одержимо систему із двома невідомими - А1 і А2 :
()
,
де uc(0)
–величина напруги на конденсаторі в
момент комутації ( при t=0)
Відповідно до другого закону комутації, напруга на конденсаторі не може змінюватися стрибком, тобто напруга відразу після комутації дорівнює напрузі до комутації:
uc(-0)=uc(0), () де uc(-0) – напруга на конденсаторі до початку комутації; uc(0) – напруга на конденсаторі при комутації
Так як. за умовою завдання конденсатор був попередньо заряджений, то напруга до комутації uc(0) = -Е В.
Для рішення системи необхідно знайти
- швидкість зміни напруги на конденсаторі
в початковий момент часу. Цю швидкість
можна визначити з формули струму через
конденсатор
, ()
де і
– струм через конденсатор;
С –
ємність конденсатора;
– швидкість зміни напруги
на конденсаторі;
Тоді для заданої схеми
, ()
де 
–
струм третьої гілки до початку комутації;
По I законі Кирхгофа
i3(0) = i1(0)
– i2(0), ()
де
–
струм третьої гілки при комутації;
–
струм першої гілки при комутації;
–
струм другої гілки при комутації;
Так як у першій гілці є котушка, то струм i1(0) у початковий момент комутації дорівнює току через котушку до комутації i1(-0) і цей струм дорівнює:
, ()
Струм другої гілці в початковий момент часу
, ()
Звідси
, ()
Виведені формули для початкових умов підставляємо в систему і знаходимо значення постійних інтегрування.
Після виконання розрахунків ми виводимо формулу для напруги на конденсаторі, записуємо її як суму вільної і примушеної складових:
, ()
де 
–
напруга на конденсаторі;
–
значення джерела ЕРС;
– величина першого опору;
– величина другого опору;
,
–
постійні інтегрування;
–
час проходження перехідного
процесу;
– корінь характеристичного рівняння;
Після виведення формули напруги на конденсаторі ми можемо знайти струм третьої гілки для цього ми беремо похідну від напруги і множимо її на ємність конденсатора, отримуємо формулу:
, ()
де
–
струм третьої гілки;
– ємність конденсатора;
–
похідна напруги на конденсаторі;
–
час проходження перехідного
процесу;
Струм другої гілки знаходиться як відношення напруги конденсатора до опору другої вітки, тому що напруга на паралельних вітках однакова, а струм дорівнює відношенню напруги до опору на якому шукається струм:
, () де – струм другої гілки; – напруга на конденсаторі; – величина другого опору;
Напруга на буде дорівнювати напрузі , тому що як я говорив напруга на паралельних вітках однакова. Струм першої гілки буде дорівнювати сумі струмів третьої і другої гілок а напруга на буде дорівнювати добутку цього опору на струм першої гілки:
, ()
де 
–
струм першої гілки;
–
струм другої гілки;
–
струм третьої гілки;
, ()
де 
–
напруга на першому опорі;
–
величина першого опору;
–
струм першої гілки;
Напругу на котушці ми можемо знайти як добуток похідної струму першої гілки на індуктивність котушки L:
, ()
де 
–
напруга на котушці;
–
індуктивність котушки;
–
похідна струму першої гілки;
Дискримінант більше нуля. Починаємо розрахунки так само як і для дискримінанта рівному нулю знаходимо характеристичний опір схеми, потім зводимо його до квадратного рівняння і знаходимо його корні, але в цьому випадку ми матимемо два різних корені, тому що дискримінант більше нуля:
, () де – корінь характеристичного рівняння; – індуктивність котушки; – ємність конденсатора; – величина другого опору; – величина другого опору; – дискримінант квадратного рівняння;
, () де – корінь характеристичного рівняння; – індуктивність котушки; – ємність конденсатора; – величина другого опору; – величина другого опору; – дискримінант квадратного рівняння;
Тепер ми можемо скласти систему для початкових умов:
()
,
запишемо ці рівняння для початкового часу(t=0)
()
,
для заданої схеми
, ()
По I законі Кирхгофа i3(0) = i1(0) – i2(0)
Так як у першій гілці є котушка, то струм i1(0) у початковий момент комутації дорівнює току через котушку до комутації i1(-0) і цей струм дорівнює:
, ()
Струм другої гілці в початковий момент часу
, ()
Звідси
, ()
Тоді ми можемо записати напругу на конденсаторі, так само як і для дискримінанта рівного нулю:
, ()
де
–
напруга на конденсаторі;
–
значення джерела ЕРС;
– величина першого опору;
– величина другого опору;
,
–
постійні інтегрування;
–
час проходження перехідного
процесу;
– корні характеристичного рівняння;
Після виведення формули напруги на конденсаторі ми можемо знайти струм третьої гілки для цього ми беремо похідну від напруги і множимо її на ємність конденсатора, отримуємо формулу:
, () де – струм третьої гілки; – ємність конденсатора; – похідна напруги на конденсаторі; – час проходження перехідного процесу;
Струм другої гілки знаходиться як відношення напруги конденсатора до опору другої вітки, тому що напруга на паралельних вітках однакова, а струм дорівнює відношенню напруги до опору на якому шукається струм:
, () де – струм другої гілки; – напруга на конденсаторі; – величина другого опору;
Напруга на буде дорівнювати напрузі , тому що як я говорив напруга на паралельних вітках однакова. Струм першої гілки буде дорівнювати сумі струмів третьої і другої гілок а напруга на буде дорівнювати добутку цього опору на струм першої гілки:
, () де – струм першої гілки; – струм другої гілки; – струм третьої гілки;
, () де – напруга на першому опорі; – величина першого опору; – струм першої гілки;
Напругу на котушці ми можемо знайти як добуток похідної струму першої гілки на індуктивність котушки L:
, () де – напруга на котушці; – індуктивність котушки; – похідна струму першої гілки;
Якщо ж дискримінант менше нуля то ми матимемо два комплексні корні. То ми знову так само знаходимо характеристичний опір схеми зводимо його до нуля і знаходимо його комплексні корні:
, () де – корінь характеристичного рівняння; – індуктивність котушки; – ємність конденсатора; – величина другого опору; – величина другого опору; – дискримінант квадратного рівняння;
, () де – корінь характеристичного рівняння; – індуктивність котушки; – ємність конденсатора; – величина другого опору; – величина другого опору; – дискримінант квадратного рівняння;
J у формулах комплексних корнів показує уявну частину комплексного числа. Там де не має J це дійсна частина комплексного числа. Після знаходження корнів характеристичного рівняння ми знову записуємо систему рівнянь для початкових умов:
()
,
Цю систему запишемо для часу t=0
()
,
для заданої схеми
, ()
По I законі Кирхгофа
i3(0) = i1(0) – i2(0),
Так як у першій гілці є котушка, то струм i1(0) у початковий момент комутації дорівнює току через котушку до комутації i1(-0) і цей струм дорівнює:
, ()
Струм другої гілці в початковий момент часу
, ()
Звідси
, ()
Тоді ми можемо записати напругу на конденсаторі:
, ()
де
–
напруга на конденсаторі;
–
значення джерела ЕРС;
– величина першого опору;
– величина другого опору;
– постійна інтегрування;
–дійсна
частина комплексного числа;
–
уявна частина комплексного числа;
–
час проходження перехідного процесу;
–
постійна інтегрування;
Струм третьої гілки знаходимо так само як і для дискримінанту дорівнює нулю, похідна напруги на конденсаторі помножена на ємність конденсатора:
, () де – струм третьої гілки; – ємність конденсатора; – похідна напруги на конденсаторі; – час проходження перехідного процесу;
Всі подальші розрахунки виконуються аналогічно до розрахунків при дискримінанту меншому нуля. Напруга на буде дорівнювати напрузі , тому що напруга на паралельних вітках однакова. Струм першої гілки буде дорівнювати сумі струмів третьої і другої гілок а напруга на буде дорівнювати добутку цього опору на струм першої гілки:
, () де – струм першої гілки; – струм другої гілки; – струм третьої гілки;
, () де – напруга на першому опорі; – величина першого опору; – струм першої гілки;
Напругу на котушці ми можемо знайти як добуток похідної струму першої гілки на індуктивність котушки L:
, () де – напруга на котушці; – індуктивність котушки; – похідна струму першої гілки;