Доказательство

Теорема доказана.

Вопрос №24

Дифференциал сложной функции. Инвариантность формы первого дифференциала.

Пусть y = f(x), x = g(t), т.е у- сложная функция.

Тогда dy = f(x)g(t)dt = f(x)dx.

 Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называетсяинвариантной формой записи дифференциала.

 Однако, если х- независимая переменная, то

dx = x, но

если х зависит от t, то х  dx.

Таким образом форма записи dy = f(x)x не является инвариантной.

 

  Пример. Найти производную функции .

 

Сначала преобразуем данную функцию: 

Вопрос №25

Дифференциалы высших порядков. Нарушение инвариантности формы второго дифференциала.

Для функции, зависящей от одной переменной    второй и третий дифференциалы выглядят так:

Отсюда можно вывести общий вид дифференциала n-го порядка от функции   :

При вычислении дифференциалов высших порядков очень важно, что   есть произвольное и не зависящее от   , которое при дифференцировании по    следует рассматривать как постоянный множитель.

Вопрос №26

Правило Лопиталя. Правило Тейлора.

Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть   или  . Тогда, если существует предел отношения производных этих функций  , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

Например, найти  . Этот предел существует  . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.

Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.

Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.

Для раскрытия неопределенностей 1^∞, 1⁰, ∞⁰ нужно прологарифмировать данную функцию и найти предел ее логарифма.

Примеры.

1. .

2. .

3. .

4. 

5. 

Обозначим  .

Прологарифмируем это равенство  . Найдем  .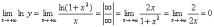

Так как lny функция непрерывная, то  . Следовательно,   или  .

ФОРМУЛА ТЕЙЛОРА

Пусть функция y= f(x) задана на (a, b) и x₀  (a, b). Поставим следующую задачу: найти многочлен P(x), значения которого в окрестности точки x₀ приближенно совпадали бы со значениями функцииf(x) в соответствующих точках. Тогда можно будет считать, что f(x)≈P(x) и задачу вычисления значенийf(x) в окрестности точки x₀ можно заменить более легкой задачей вычисления значений P(x).

Пусть искомый многочлен имеет степень n P(x) = P_n(x). Будем искать его в виде

(1)

В этом равенстве нам нужно найти коэффициенты  .

Для того чтобы этот многочлен был "близок" к функции f(x) потребуем выполнения следующих равенств:

Пусть функция y= f(x) имеет производные до n-ого порядка. Найдем коэффициенты   многочлена P_n(x) исходя из условия равенства производных.

Введем обозначение n! = 1·2·3…n, 0! = 1, 1! = 1.

Подставим в (1) x = x₀ и найдем  , но с другой стороны  . Поэтому 

Далее найдем производную   и вычислим   Следовательно,  .

Учитывая третье условие и то, что

,

получим  , т.е.  .

Далее 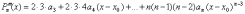 . Значит,  , т.е.  .

Очевидно, что и для всех последующих коэффициентов будет верна формула 

Подставляя найденные значения коэффициентов   в формулу (1), получим искомый многочлен:

Обозначим   и назовем эту разность n-ым остаточным членом функции f(x) в точке x₀. Отсюда   и, следовательно,   если остаточный член будет мал.

Оказывается, что если x₀  (a, b) при всех x  (a, b) существует производная f ⁽ⁿ⁺¹⁾(x), то для произвольной точки x  (a, b) существует точка, лежащая между x₀ и x такая, что остаток можно представить в виде:

Это так называемая формула Лагранжа для остаточного члена.

Формула

 где x  (x₀, x) называется формулой Тейлора.

Если в этой формуле положить x₀ = 0, то она запишется в виде

где x  ( x₀, x). Этот частный случай формулы Тейлора называют формулой МакЛорена.