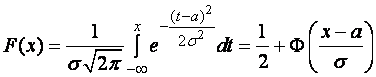15. Довести основні властивості математичного сподівання і дисперсії.

Основні властивості математичного сподівання

Математичне сподівання постійної величини дорівнює самій постійній М(С) = С.

Постійний множник можна виносити за знак математичного сподівання М(СХ)=С*М(Х).

Математичне сподівання добутку декількох взаємно незалежних дискретних випадкових величин дорівнює добутку їх математичних сподівань, тобто М(Х1*Х2*…*Хn) = М(Х1)*М(Х2)*…*М(Хn).

Математичне сподівання суми випадкових величин дорівнює сумі їх математичних сподівань, тобто М(Х1+Х2+…+Хn ) = М(Х1)+М(Х2)+…+М(Хn)

Основні властивості дисперсії.

1)Дисперсія будь-якої ДВВ Х невід’ємна

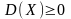
Дійсно, (Х – М(Х))2 невід’ємна, тому згідно означення математичного сподівання та властивостей pk , k =1,2, … , n , D(X) також невід’ємна.

2)Дисперсія постійної величини С дорівнює нулеві

D(X) = 0

Дійсно, якщо Х=С, то М(С)= С, тому С – М(С) = 0

3)Постійний множник С можна виносити за знак дисперсії, при цьому постійний множник треба піднести у квадрат

D(СX) = С2 D(X).

Дійсно, СХ – М(СХ) = С (Х – М(Х)), тому

(СХ – М(СХ))2 = С2 (Х – М(Х))2.

Постійний множник С2 можна виносити за знак математичного сподівання, тому з формули D(X) = М((Х – М(Х))2) випливає потрібна рівність D(СX) = С2 D(X).

4) Дисперсія ДВВ Х дорівнює різниці між математичним сподіванням квадрата випадкової величини Х та квадрата її математичного сподівання

D(X) = М(Х2) – (М(Х))2.

Дійсно, D(X) = М((Х – М(Х))2) = М(Х2 – 2ХМ(Х) + М2(Х)) = М(Х2) – 2М2(Х) + М2(Х) = М(Х2) - М2(Х).

5) дисперсія алгебраїчної суми ДВВ Х та Y дорівнює сумі їх дисперсій

16. Записати основні закони розподілу д.В.В.: а) біноміальний ; б)Пуассона; в)геометричний; г) гіпергеометричний. Пояснити зміст букв. Навести приклади д.В.В., розподілених за цими законами.

1. Біноміальний

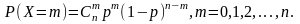
2.Пуассона

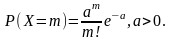
3.Геометричний

.

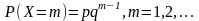4. Гіпергеометричний

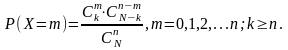
17. Рівномірний.Величина Х розподілена рівномірно у проміжку (a,b), якщо усі її можливі значення належать цьому проміжку і щільність її імовірностей у цьому проміжку постійна, тобто

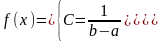
При х (a,b),

При х (a,b).

Величина 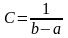визначається умовою нормування Р(а< X<b) = C(a - b) = 1

Імовірність влучення Х в інтервал (х1, х2) дорівнює відношенню довжини цього інтервалу до довжини усього проміжку (a,b).

Цей розподіл задовольняють, наприклад, похибки округлення різноманітних розрахунків. С=const

18. Нормальний закон розподілу (або закон Гауса). Закон розподілу ймовірностей неперервної ВВ Х називається нормальним законом або законом Гауса з параметрами  , якщо його щільність розподілу рівна:

,

де   - сталі. Коротко позначають  ~ .

Нормальний розподіл з параметрами   називається стандартним. Щільність розподілу ВВ в цьому випадку буде:

.

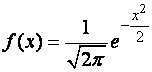Для нормально розподіленої ВВ Х з параметрами  :

Функція розподілу	Матем. сподівання	Дисперсія

Ймовірність попадання в інтервал   нормально розподіленої ВВ Х знаходиться за формулою:

,

де 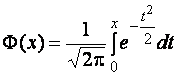    - нормована функція Лапласа (значення функції дивись в додатку 1). Її властивості: функція   - непарна, тобто  ;  ;  .

Нормальний закон широко застосовується на практиці. За його допомогою описують похибки вимірювань різних фізичних величин, лінійні розміри, масу і багато параметрів деталей при масовому виробництві.