
- •I. Электростатика
- •§1. Электрические заряды. Закон сохранения заряда. Закон Кулона. Принцип суперпозиции.
- •§2. Напряженность электрического поля в вакууме. Поле точечного заряда. Принцип суперпозиции для напряженности поля.
- •§3. Применение принципа суперпозиции для расчёта полей.
- •§4. Работа в электростатическом поле. Разность потенциалов. Потенциал электрического поля. Связь потенциала с напряжённостью поля. Принцип суперпозиции для потенциала
- •§5. Поток вектора напряжённости. Теорема Гаусса для электростатического поля в вакууме.
- •§6. Проводники и диэлектрики.
- •§7. Электрический диполь. Поле диполя.
- •§8. Диполь в электрическом поле. Сила и момент силы, действующие на диполь в электрическом поле. Энергия диполя в электрическом поле.
- •§9. Диэлектрики в электрическом поле. Поляризация диэлектрика. Вектор поляризации. Диэлектрическая восприимчивость.
- •§10. Теорема Гаусса для электростатического поля в диэлектрике. Диэлектрическая проницаемость. Вектор d
- •§ 11. Условия для электростатического поля на границе раздела диэлектриков
- •§12. Проводники в электростатическом поле
- •§13. Электроемкость
- •§14. Энергия электростатического поля
- •II. Постоянный электрический ток
- •§1. Электрический ток. Природа электрического тока в различных средах. Сила и плотность тока. Уравнение неразрывности.
- •§2. Классическая электронная теория металлов.
- •§3. Подвижность носителей заряда. Проводимость. Закон Ома в локальной и интегральной формах. Эдс. Напряжение.
- •§4. Закон Джоуля-Ленца в локальной и интегральной формах.
- •§5. Закон Видемана-Франца.
- •§6. Трудности классической электронной теории металлов.
- •§7. Расчет разветвленных цепей постоянного тока. Правила Кирхгофа.
- •III. Электромагнетизм
- •§ 1. Магнитное поле. Закон Ампера
- •§ 2. Закон Био-Савара-Лапласа Принцип суперпозиции для вектора
- •§ 3. Применение принципа суперпозиции
- •§ 4. Взаимодействие параллельных токов. Единица силы тока 1 а
- •§ 5. Закон полного тока для магнитного поля в вакууме
- •§ 6. Применение закона полного тока для вычисления магнитного поля
- •§ 7. Действие магнитного поля на движущийся заряд. Магнитное взаимодействие зарядов
- •§ 8. Движение заряженных частиц в магнитном поле
- •§ 9. Работа по перемещению проводника с током в магнитном поле. Магнитный поток. Потокосцепление
- •§ 10. Магнитный момент контура с током. Контур с током в магнитном поле
- •§ 11. Магнитный момент атома. Атом в магнитном поле
- •§ 12. Вещество в магнитном поле. Намагниченность.
- •§ 13. Циркуляция вектора намагниченности
- •§ 14. Закон полного тока для магнитного поля в веществе
- •§ 15. Ферромагнетики
- •§ 16. Магнитомеханический эффект. Спин электрона
- •§ 17. Теорема Гаусса для магнитного поля
- •§ 18. Условия для магнитного поля на границе раздела магнетиков
- •§ 19. Явление электромагнитной индукции
- •§ 20. Заряд, индуцированный в явлении электромагнитной индукции.
- •§21. Явление самоиндукции. Индуктивность.
- •§22. Вихревые токи. Скин-эффект.
- •§23. Взаимная индукция. Коэффициент взаимной индукции.
- •§ 24. Энергия магнитного поля
- •IV. Уравнения максвелла для электромагнитного поля
- •§ 1. Первое уравнение Максвелла
- •§ 2. Второе уравнение Максвелла. Ток смещения
- •§ 3. Третье и четвертое уравнения Максвелла
- •§4. Полная система уравнений Максвела для электромагнитного поля
IV. Уравнения максвелла для электромагнитного поля
§ 1. Первое уравнение Максвелла
Стороннее поле
![]() ,
возникающее в проводниках в соответствии
с явлением электромагнитной индукции,
по предположению Максвелла возникает
и в отсутствии проводников:
,
возникающее в проводниках в соответствии
с явлением электромагнитной индукции,
по предположению Максвелла возникает
и в отсутствии проводников:
![]() (1.1).
(1.1).
Кроме того,
![]() ,
поэтому для любого электрического поля
,
поэтому для любого электрического поля
![]()
![]() (1.2)
(1.2)
(1.2) –
первое
уравнение Максвелла в интегральной
форме. От
уравнения (1.2) можно перейти к
дифференциальному уравнению для
![]()
![]() (1.3)
(1.3)
(1.3) - первое уравнение Максвелла в дифференциальной форме.
§ 2. Второе уравнение Максвелла. Ток смещения
Пусть ток i
создаётся в проводнике заряженным
конденсатором С.
Запиш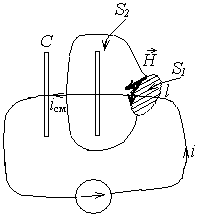 ем
закон полного тока (14.4) для контура l
ем
закон полного тока (14.4) для контура l
![]() .
(2.1)
.
(2.1)
Очевидно, в
пространстве существует магнитное
поле, и интеграл (2.1) отличен от нуля. Он
просто равен току i,
который можно посчитать с помощью
интеграла
![]()
0. Однако, если для нахождения тока i
в (2.1) выбрать поверхность интегрирования
S2,
находящуюся между обкладками конденсатора,
где носители заряда отсутствуют то
0. Однако, если для нахождения тока i
в (2.1) выбрать поверхность интегрирования
S2,
находящуюся между обкладками конденсатора,
где носители заряда отсутствуют то
![]() и интеграл (2.1) формально равен нулю. Но
это невозможно, ведь его значение
определяется только полем
.
Значит существует некоторая величина,
которую следует использовать в интеграле
(2.1) вместо
и интеграл (2.1) формально равен нулю. Но
это невозможно, ведь его значение
определяется только полем
.
Значит существует некоторая величина,
которую следует использовать в интеграле
(2.1) вместо
![]() и которая связана с током i
и имеет внутри конденсатора отличное
от нуля значение. Найдём эту физическую
величину.
и которая связана с током i
и имеет внутри конденсатора отличное
от нуля значение. Найдём эту физическую
величину.
Для направления тока, указанного на рисунке, заряд конденсатора С увеличивается:
![]() .
(2.2)
.
(2.2)
Заряд q
создает в конденсаторе электрическое
смещение
![]() .
В соответствии с (10.3) q=
.
В соответствии с (10.3) q=
![]() .
Подставляя q
в (2.2), получаем
.
Подставляя q
в (2.2), получаем
![]() .
(2.3)
.
(2.3)
Величину
![]() в
(2.3) называют
током смещения.
На рисунке ток проводимости i
в проводнике замыкается в конденсаторе
таким же по величине в соответствии с
(2.2) током
смещения
в
(2.3) называют
током смещения.
На рисунке ток проводимости i
в проводнике замыкается в конденсаторе
таким же по величине в соответствии с
(2.2) током
смещения
![]() .
(2.4)
.
(2.4)
Теперь (2.1) выполняется
при любом выборе поверхности S.
Другими словами магнитное поле можно
вычислить и с использованием
![]() .
Максвелл предположил, что ток смещения
– а именно меняющееся поле
- порождает магнитное поле точно так
же, как и токи проводимости, т.е. под
током i
в (2.1) следует понимать
.
Максвелл предположил, что ток смещения
– а именно меняющееся поле
- порождает магнитное поле точно так
же, как и токи проводимости, т.е. под
током i
в (2.1) следует понимать
iполн
=![]() .
(2.5)
.
(2.5)
![]() .
(2.6)
.
(2.6)
Это второе уравнение Максвелла в интегральной форме. Из (2.6) можно получить второе уравнение в дифференциальной форме
![]() .
(2.7)
.
(2.7)
Уравнения (1.3) и (2.7) указывают на неразрывную связь переменных электрического и магнитного полей.
