§ 6. Применение закона полного тока для вычисления магнитного поля

С помощью закона полного тока в интегральной форме несложно вычислить магнитное поле симметричных систем с током I. Например:

1. Поле прямого тока B = .

2. Поле тороида B =

3. Поле соленоида B =

§ 7. Действие магнитного поля на движущийся заряд. Магнитное взаимодействие зарядов

На элемент тока в магнитном поле действует сила Ампера . Ток I = jS = nq^.S создан движущимися в объеме (S^.dl) элемента тока зарядами q с концентрацией n: dN = nSdl

.

Сила, действующая на отдельный заряд q со стороны магнитного поля , т.е. . При наличии электрического поля полная сила, действующая на заряд, равна

(7.1)

Рис.7.1. и носит название силы Лоренца.

Рассмотрим взаимодействие двух зарядов q₁ и q₂, движущихся со скоростями ₁, ₂ << c.

Со стороны первого заряда на второй действует сила и

.

Найдем поле , создаваемое отдельным зарядом q₁ из следующих соображений

. (7.2)

Тогда Очевидно, максимальное значение силы равно

(7.3)

Вычисление магнитной и электрической составляющих силы Лоренца показывает, что << .

§ 8. Движение заряженных частиц в магнитном поле

В простейшем случае движение под действием по окружности радиуса R

(8.1)

Рис.8.1. (8.2)

§ 9. Работа по перемещению проводника с током в магнитном поле. Магнитный поток. Потокосцепление

П ри перемещении элемента тока на сила Ампера совершает работу

(9.1)

Величина

(9.2)

называется элементарным потоком вектора магнитной индукции через элементарную площад-

Рис.9.1 ку dS.

Н аправления обхода площадки и вектора связывают правилом правого винта. При перемещении контура с постоянным неменяющимся по величине током совершается работа

. (9.3)

Рис.9.2 Если контур состоит из нескольких витков, то работа (9.3) равна где величина

(9.4)

называется потокосцеплением.

§ 10. Магнитный момент контура с током. Контур с током в магнитном поле

По определению, элементарный магнитный момент

. (10.1)

Магнитный момент плоского контура

. (10.2)

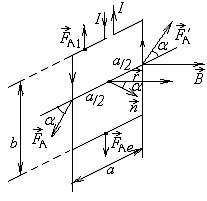1. Вычислим вращающий момент, действующий на контур с током в магнитном поле

, направлен вверх.

.

Учитывая направления векторов

. (10.3)

Момент сил разворачивает кон-тур так, чтобы направления и совпали.

Рис. 10.2

2. По аналогии с электрическим диполем, для которого и запишем выражения для силы, действующей на контур с током,

(10.4)

и энергии контура в магнитном поле

(10.5)