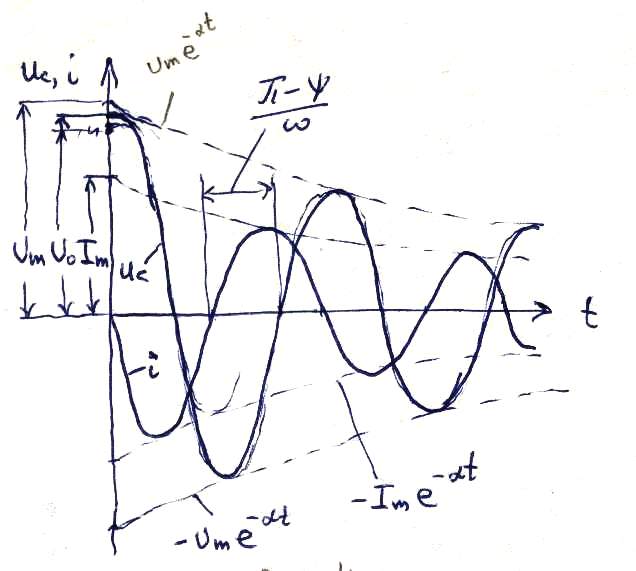
4.4.2. Периодический переходной процесс

Он имеет место при ,когда корни характеристического уравнения комплексно-сопряженные ; . Тогда решение дифференциального уравнения . Соответственно .

Подставив начальные условия, получим:

Откуда

; .

Обозначив , и учитывая, что

; ,

получим

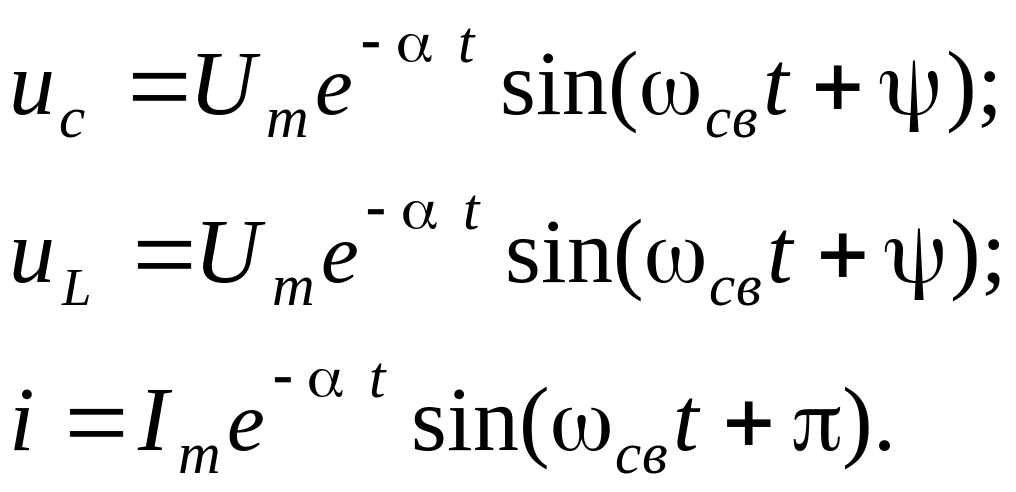
Заметим, что также как и начальная фаза зависит только от параметров контура. Скорость затухания колебаний характеризуют величиной , которая называется декрементом колебания. Иногда используют понятие логарифмического декремента колебания: .

При увеличении сопротивления увеличивается и период колебания, и когда достигает период равен бесконечности, то есть наступает апериодический процесс. При : , ; 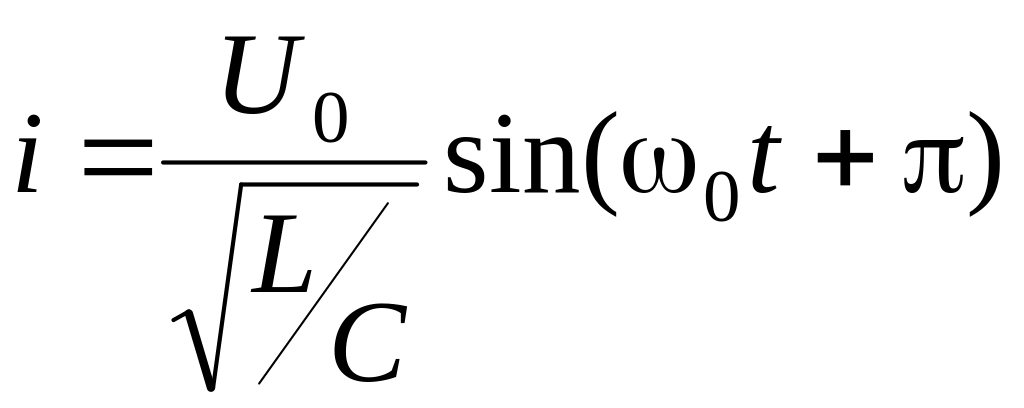, то есть частота максимальна и равна резонансной частоте

последовательного контура.

Рис. .4.10.

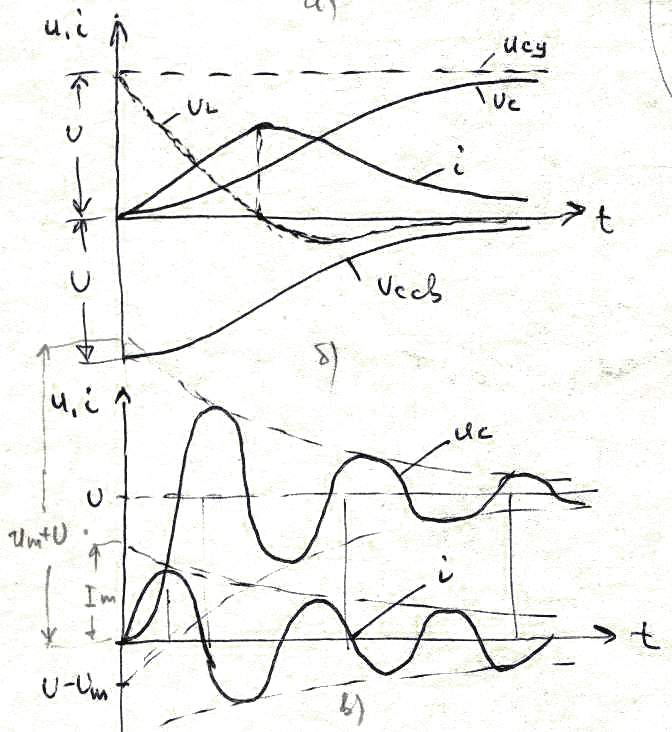
4.4.3. Переходной процесс в -цепи при включении на постоянное напряжение

Рис. 4.11.

Установившийся ток в схеме по рис.4.11а также равен нулю, однако установившееся напряжение на конденсаторе (рис.4.11.б,в). Поскольку то знаки коэффициентов и изменяются на обратные. При колебательном характере процесса (риc.4.11.в) затухающие колебания тока происходят относительно нулевого значения, а напряжение колеблется относительно и не может превысить

С энергетической точки зрения при включении -цепи на постоянное напряжение половина энергии, получаемая от источника питания за время периодического переходного процесса переходит в тепло, а другая половина запасается в электрическом поле конденсатора.

Аналогично может быть рассмотрен апериодический и колебательный процесс при включении контура на синусоидальное напряжение:

4.5. Расчет переходных процессов классическим методом

Классический метод расчета основан на составлении дифференциальных уравнений и их интегрировании. Уравнение составляются относительно мгновенных значений напряжения и тока и называются уравнениями состояния.

Полное решение уравнений состояния ищется как сумма установившихся и свободных составляющих напряжений и токов. Для этого находят соответственно частное решение системы неоднородных уравнений и общее решение однородных, приравнивая нулю правые части.

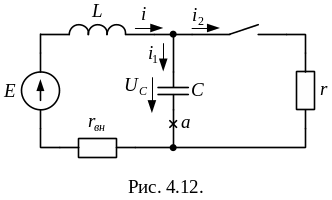
Рассмотрим порядок расчета на примере. Будем искать в схеме по рис.4 как

.

По первому и второму законам Кирхгофа составим систему уравнений для цепи после коммутации.

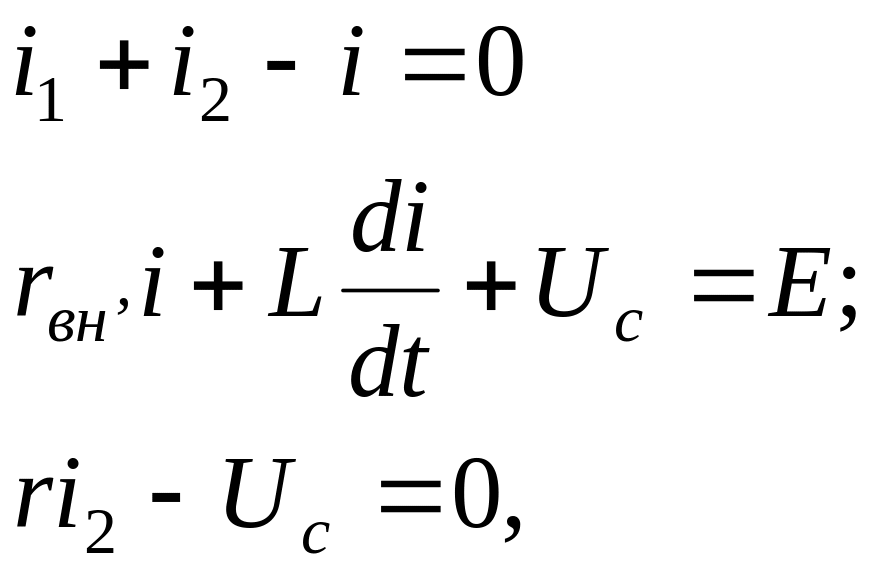где . Или

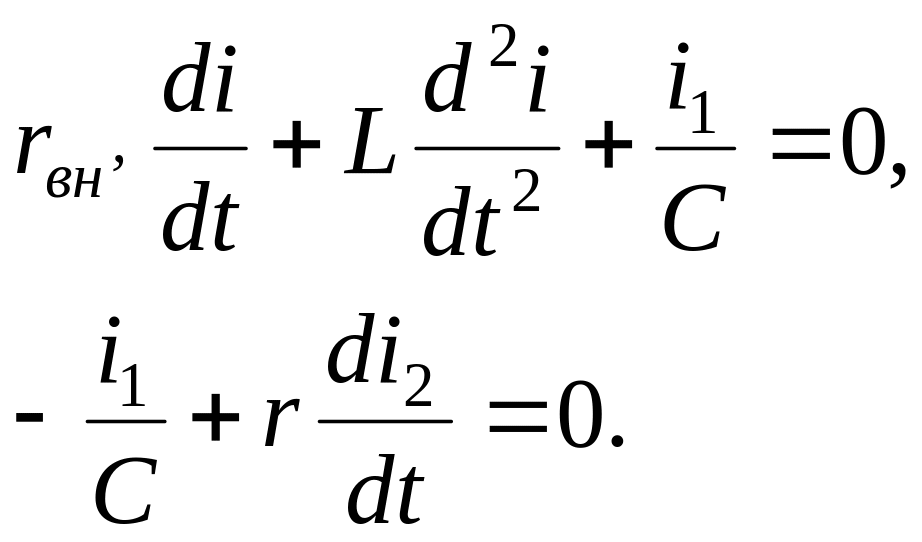
Для нахождения начальных условий ( ), рассчитаем цепь до коммутации.

Рассчитаем установившийся режим после коммутации.

Для расчета свободной составляющей тока воспользуемся алгебраизацией однородных дифференциальных уравнений и приравняем к нулю главный определитель системы.

где соответствует установившемуся режиму, который мы уже нашли.

Уравнение, полученное в результате приравнивания нулю главного определителя, называется характеристическим уравнением. Как уже было показано выше корни характеристического уравнения определяют характер переходного процесса. Это характеристическое уравнение может быть получено и при составлении системы по методу контурных токов или узловых потенциалов.

Более того, характеристическое уравнение можно получить и без составления системы дифференциальных уравнений. Для этого достаточно записать и приравнять нулю комплексное входное сопротивление цепи относительно разрыва в любой ветви и заменить оператором . Например, разорвав цепь в цепи конденсатора (точка а), получим входное сопротивление

или

что соответствует уже полученному нами уравнению.

Запишем свободную составляющую с постоянными интегрирования, в зависимости от вида корней: действительные разные , равные

, комплексно-сопряженные .

Записываем общее решение. Пусть, например, корни действительные и разные, тогда

Определим постоянные интегрирования. Для этого запишем и при :

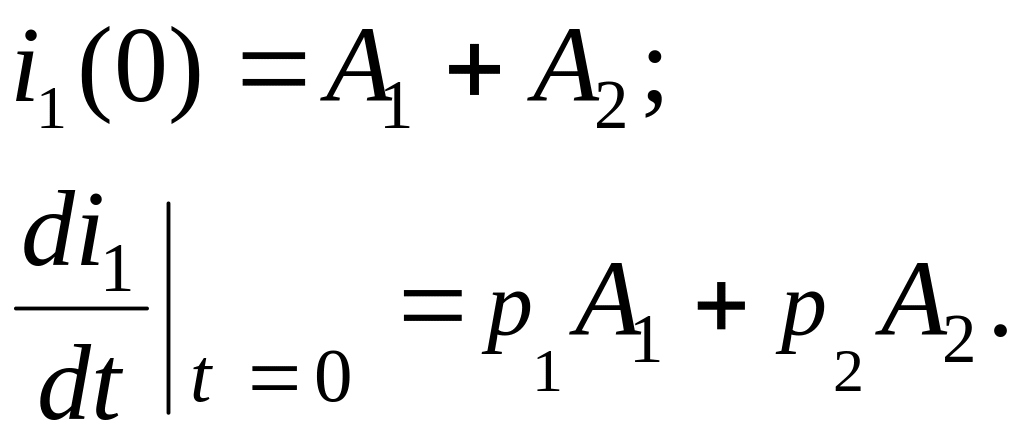
Запишем систему уравнений для момента t=0. Здесь и уже известны. Таким образом, имеем три уравнения с тремя неизвестными. Откуда легко определить .

7⁰. После определения и подставляем их в искомое решение.