4.3. Переходные процессы в -цепи

а) Короткое замыкание в -цепи

Пусть конденсатор, заряженный до напряжения (рис.4.5.а), после коммутации разрежается через резистор .

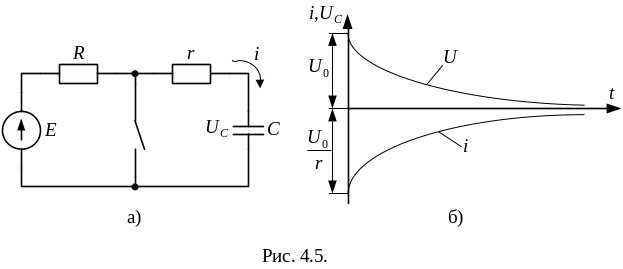
Установившиеся ток и напряжение на конденсаторе равны нулю, то есть нужно найти только свободные составляющие.

.

По второму закону Кирхгофа: . Тогда получаем однородное дифференциальное уравнение первого порядка: . Решение , так как — постоянная времени, то , где — коэффициент затухания.

Начальные условия , то есть , (см. рис.4.5,б).

С энергетической точки зрения энергия, запасенная в конденсаторе вся переходит в тепло . Заметим, что так как любая емкость на практике имеет некоторую индуктивность, ток реально начнется с нуля, но очень быстро достигнет значения близкого к .

б) Включение -цепи на постоянное напряжение

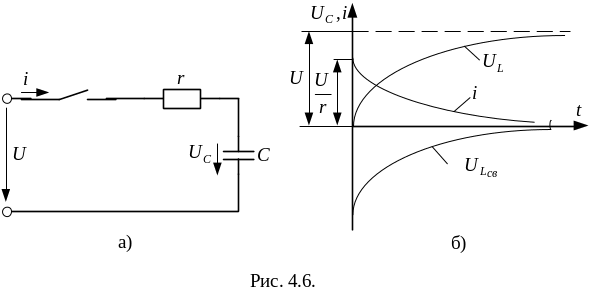
По второму закону Кирхгофа (рис.4.6.а): или

Так как свободный процесс тот же: .

При : , , тогда , а (смотри рис.4.6.б).

в) Включение -цепи на синусоидальное напряжение

При входном напряжении установившееся напряжение на емкости , где ,

Свободный процесс тот же, тогда

.

Начальные условия , откуда , тогда

,

.

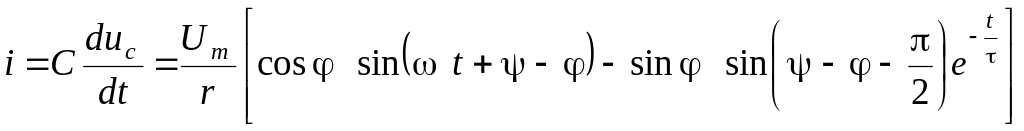Полученные соотношения иллюстрируются рис.4.7.

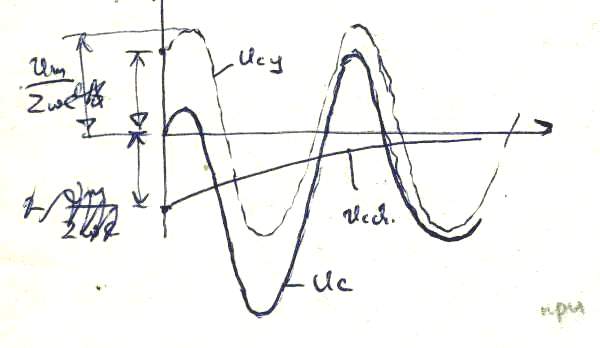
Рис. 4.7.

Во время переходного процесса напряжение на емкости может достигать удвоенной амплитуды напряжения установившегося процесса. Поэтому необходимо учитывать, что при коммутациях в цепях с емкостью возможны большие выбросы тока. Например, при коммутации низкоомных цепей, имеющих значительную емкость на землю.

4.4. Переходные процессы в последовательном контуре

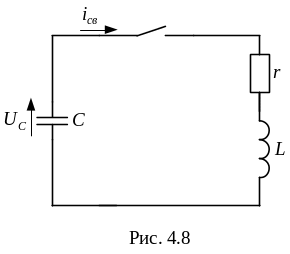
Для последовательного контура (см. рис.4.8) при отсутствии источников (т.е. когда , ) по второму закону Кирхгофа: , где . Или , аналогичное дифференциальное уравнение второго порядка получается и для тока (заряда). Характеристическое уравнение : . Характер свободного процесса зависит от знака подкоренного выражения, и может быть либо апериодическим, либо периодическим.

4.4.1. Апериодический переходной процесс

При таком процессе напряжение на конденсаторе монотонно спадает от до 0, то есть энергия конденсатора в основном переходит в тепло (резистор), и, лишь в малой дозе, в энергию магнитного поля катушки, которая начиная с некоторого момента времени также переходит в тепло. Описанный процесс имеет место, если корни характеристического уравнения действительные, то есть или , где — критическое сопротивление: .

При корни и действительные и различные, тогда решение однородного дифференциального уравнения , , где и постоянные интегрирования, определяемые из начальных условий, а и всегда отрицательные, так как свободный процесс должен быть затухающим.

Учитывая, что , получим

, .

Тогда : (т.к. ).

Напряжение на индуктивности .

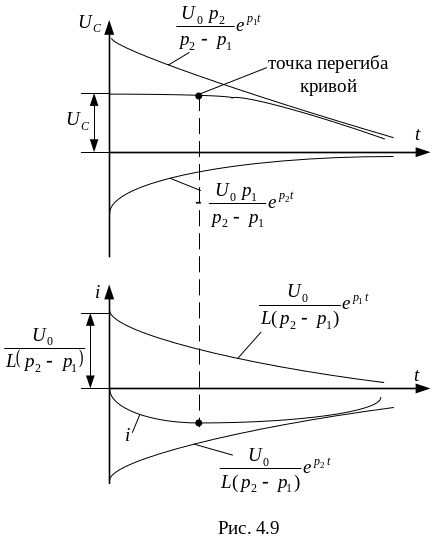
Таким образом, ток и напряжение на индуктивности и емкости состоят из двух экспоненциальных составляющих с разными постоянными времени (см. рис.4.9).

Ток возрастает от нуля до некоторого максимума, а затем уменьшается. Решив уравнение , можно найти и время, соответствующего максимального тока.

Касательная к кривой напряжения в начале координат горизонтальна.

При , то есть при равных и действительных корнях характеристического уравнения , получим ; . Это предельный случай апериодической разрядки. Учитывая, что и находим, что , . Тогда .