- •4. Переходные процессы в цепях с сосредоточенными параметрами
- •4.1. Основные понятия и законы
- •4.2. Переходные процессы в -цепи
- •4.3. Переходные процессы в -цепи
- •4.4. Переходные процессы в последовательном контуре
- •4.4.1. Апериодический переходной процесс
- •4.4.2. Периодический переходной процесс
- •4.4.3. Переходной процесс в -цепи при включении на постоянное напряжение
- •4.5. Расчет переходных процессов классическим методом
- •Примечание:
- •4.6. Переходная и импульсная характеристики цепи
- •4.7. Использование интеграла Дюамеля при анализе реакции цепи на произвольно имеющееся входное воздействие
- •4.8. Расчет переходных процессов операторным методом.
- •Тогда в операторной форме
- •5. Четырехполюсники и многополюсники
- •5.1. Введение. Первичные параметры чп
- •5.2. Экспериментальное определение коэффициентов и входного сопротивления
- •5.3. Эквивалентные схемы четырехполюсников
- •5.4. Соединения четырехполюсников
- •5.5. Передаточные функции и рабочие параметры четырехполюсника
- •5.6. Зависимые источники напряжения и тока
- •5.7. Вторичные параметры пассивных четырехполюсников
- •5.8. Активные автономные чп
- •5.9. Операционный усилитель (оу)
- •6. Цепи с распределенными параметрами
- •6.1. Первичные параметры длинной линии
- •6.2 Телеграфные и волновые уравнения дл. Вторичные параметры дл.
- •6.3. Бегущие, стоячие и смешанные волны в дл
- •6.3.1. Бегущие волны
- •6.3.2. Стоячие волны
- •6.3.3. Смешанные волны
- •6.4. Переходные волновые процессы
- •6.5. Волновые параметры дл
- •6.6. Сбалансированная дл
- •6.7. Резонансные чп. Примеры использования дл
- •6.8. Согласующие чп
6.3.2. Стоячие волны
Если
в ДЛ без потерь
![]() .
Равенство амплитуд означает, что энергия
не потребляется нагрузкой, т.е. линия
либо нагружена на реактивное сопротивление,
либо замкнута, либо разомкнута.
.
Равенство амплитуд означает, что энергия
не потребляется нагрузкой, т.е. линия
либо нагружена на реактивное сопротивление,
либо замкнута, либо разомкнута.
![]() ,
,
![]() .
.
Т.к. в линии без потерь сопротивление активно,
![]() ,
,
![]() .
.
Сложив
![]() и
и
![]() ,
,
![]() и
и
![]() ,
получим,
,
получим,
![]() ,
,
![]() ,
,
где
![]() ;
;
![]()
Т.к.
у этих волн фазы не перемещаются вдоль
линии, то такие волны называются стоячими.
Их амплитуда изменяется вдоль линии от
![]() до
до
![]() .
Эти нули и максимумы называются
соответственно узлами
и пучностями
стоячих волн. А фазы волн изменяются
вдоль линии скачком на
.
Эти нули и максимумы называются
соответственно узлами
и пучностями
стоячих волн. А фазы волн изменяются
вдоль линии скачком на
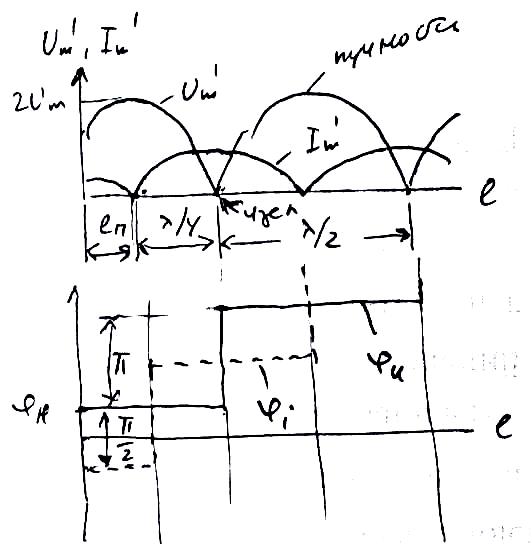
![]() при изменении знака амплитуд. Кроме
того, фазы напряжения и тока сдвинуты
на
при изменении знака амплитуд. Кроме
того, фазы напряжения и тока сдвинуты
на
![]() (рис. 6.6.), т.е. пучности напряжения
совпадают с узлами тока и наоборот.
Ближайшая к концу линии пучность
н
находиться
на расстоянии
(рис. 6.6.), т.е. пучности напряжения
совпадают с узлами тока и наоборот.
Ближайшая к концу линии пучность
н
находиться
на расстоянии
![]() (из условия
(из условия
![]() ).
).
|
Рис. 6.6. |
6.3.3. Смешанные волны
Опять
будем считать, что ДЛ без потерь, а часть
энергии расходуется в нагрузке, т.е.
![]() .
Представим
двумя составляющими
.
Представим
двумя составляющими
![]() и
и
![]() .
Тогда
.
Тогда
![]() образуют стоячую волну. Т.е. можно
считать:
образуют стоячую волну. Т.е. можно
считать:
![]() .
.
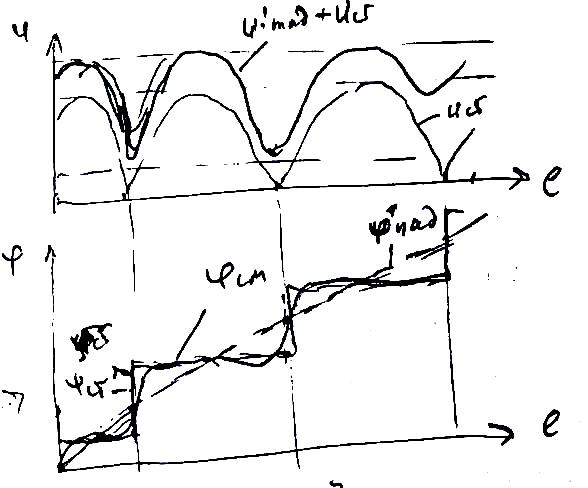
Такая суперпозиция бегущей и стоячей волны получила название смешанной волны. Амплитуда и фаза смешанной волны плавно изменяются вдоль линии (рис. 6.7). Пучностям и узлам стоячей волны соответствует максимальное и минимальное значения амплитуд волны смешанной.
|
Рис. 6.7. |
Для характеристики смешанных волн используют коэффициенты бегущей (КБВ) и стоячей (КСВ) волн.
![]() ,
,
![]()
(Показывает во сколько раз одна амплитуда превышает другую).
Если
![]() ,
то
,
то
![]() .
Левые границы соответствуют режиму
бегущих волн, правые - стоячих.
.
Левые границы соответствуют режиму
бегущих волн, правые - стоячих.
Заметим,
что
![]() и
и
![]() легко определяются экспериментально
измерением максимальной и минимальной
амплитуд смешанных волн.
легко определяются экспериментально
измерением максимальной и минимальной
амплитуд смешанных волн.
В линиях с потерями падающие и отражающиеся волны носят затухающий характер и волновой процесс в линии является более сложным. Для его анализа введем коэффициент отражения
![]() ,
,
(т.к.
![]() ,
то
,
то
![]() ),
где
),
где
![]() - коэффициент отражения на конце линии
(в нагрузке).
- коэффициент отражения на конце линии
(в нагрузке).
![]() ,
,
![]() .
.
Выразим
![]() через коэффициент отражения.
через коэффициент отражения.
 ,
,
![]() .
.
Из
выражения видно, что при
![]() в любом сечении ДЛ
в любом сечении ДЛ
![]() - это режим бегущих волн, т.к. отраженная
волна отсутствует. Такая линия называется
согласованной,
а
- условия
согласования.
В несогласованной линии
- это режим бегущих волн, т.к. отраженная
волна отсутствует. Такая линия называется
согласованной,
а
- условия
согласования.
В несогласованной линии
![]() и убывает в направлении к входу. При
достаточной длине линии
и убывает в направлении к входу. При
достаточной длине линии
![]() .
Соответственно в разных сечениях будет
разным и КБВ.
.
Соответственно в разных сечениях будет
разным и КБВ.
 ,
,
![]() .
.
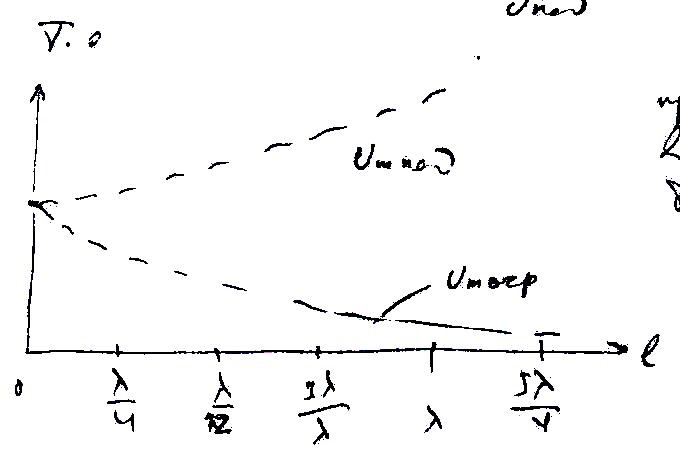
Ближе к нагрузке волновой процесс может быть близок к режиму стоячих волн, ближе ко входу - режим бегущих волн.
|
Рис. 6.8. |
6.4. Переходные волновые процессы
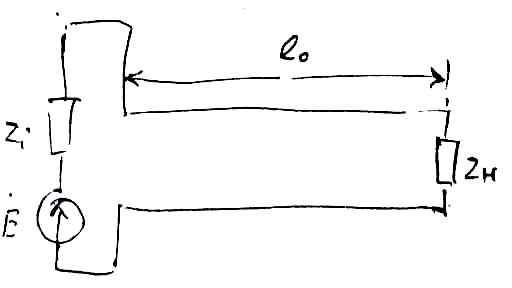
|
Рис. 6.9. |
При
включении ЭДС на входе ДЛ возникает
бегущая волна
![]() ,
которая распространяется с фазовой
скоростью
,
которая распространяется с фазовой
скоростью
![]() ,
которая через время
,
которая через время
![]() доходит до конца линии и отражается,
образуя
доходит до конца линии и отражается,
образуя
![]() .
Через
она достигает входа и вновь отражается,
создавая
.
Через
она достигает входа и вновь отражается,
создавая
![]() и т.д. до бесконечности.
и т.д. до бесконечности.
В
пределе ( при
![]() )
)
![]() ,
,
![]() .
.
коэффициент отражения от конца ДЛ

определяется
несогласованностью нагрузочного и
волнового сопротивлений, а в начале
линии – внутреннего сопротивления
источника
![]() и волнового сопротивления.
и волнового сопротивления.
![]() .
.
Отметим,
что следует отличать коэффициент
отражения как функцию длины линии
![]() и коэффициенты отражения от нагрузки
в входа ДЛ. В частности, коэффициент
отражения на конце линии
и коэффициенты отражения от нагрузки
в входа ДЛ. В частности, коэффициент
отражения на конце линии
![]() и от нагрузки равны, а в начале
и от нагрузки равны, а в начале
![]() и от входа не равны.
и от входа не равны.
|
Рис. 6.10 |
Пример.
Пусть ДЛ без потерь и
![]() .
В момент
.
В момент
![]() включаем ЭДС с
включаем ЭДС с
![]() .
Тогда
.
Тогда
![]() ;
;
![]() ;
;
![]() ;
;
![]() при
при
![]() ,
,
![]() -
волновое сопротивление
-
волновое сопротивление
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
т.е. дальше процесс повторяется.
Рассмотрим
напряжение
![]() на выходе и токи
на выходе и токи
![]() на входе ДЛ.
на входе ДЛ.
Моменты
отражения от выхода соответствуют
,
![]() ,
,
![]() ...
Тогда
...
Тогда
![]()
![]() ,
,
![]()
Для тока на входе
![]()
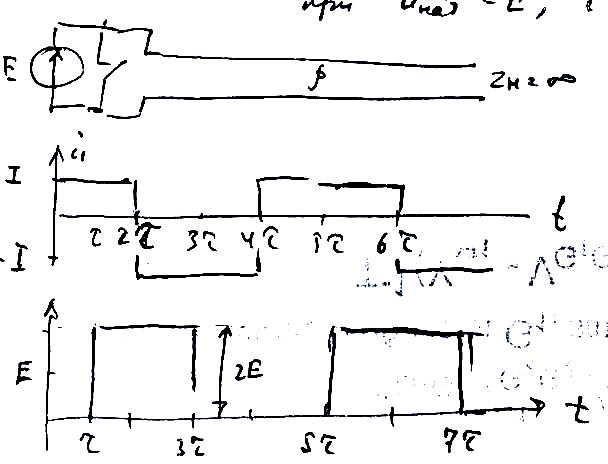
Таким
образом, в ДЛ без потерь при
![]() возникают прямоугольные колебания с
периодом
возникают прямоугольные колебания с
периодом
![]() .
Соответственно длина волны в этой линии
.
Соответственно длина волны в этой линии
![]() .
Это случай разноименных
граничных условий
на входе и выходе ДЛ (
-
режим х.х.,
- режим к.з.).
.
Это случай разноименных
граничных условий
на входе и выходе ДЛ (
-
режим х.х.,
- режим к.з.).
|
Рис. 6.11 |
Рассмотрим
колебания при одноименных граничных
условиях
![]() .
Для этого на входе нужно вместо источника
напряжения включить источник тока,
тогда
.
Для этого на входе нужно вместо источника
напряжения включить источник тока,
тогда
![]() ,
,
![]() .
.
В
сечении линии на расстоянии
![]() от входа падающие волны будут в моменты
от входа падающие волны будут в моменты
![]() ,
а отражения
,
а отражения
![]() ,
,
![]() ,
,
![]() .
Т.к.
.
Т.к.
![]() и
и
![]() имеют разные знаки, то в выбранном
сечении с периодом
имеют разные знаки, то в выбранном
сечении с периодом
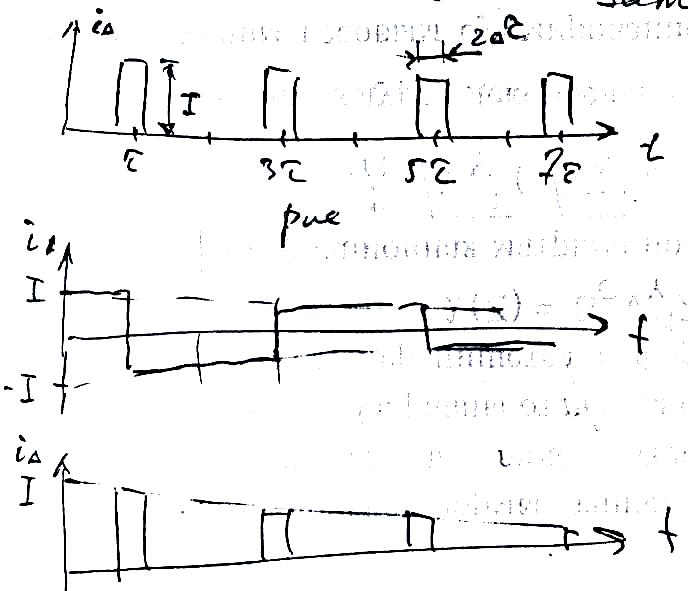
![]() возникнут импульсные токи
возникнут импульсные токи
![]() с амплитудой
с амплитудой
![]() .
Заметим, что этой длине волны
.
Заметим, что этой длине волны
![]() .
Таким образом, длинные линии обладают
колебательными свойствами. При этом
при разноименных граничных условиях в
ДЛ укладывается четверть волн, а при
одноименных - половина. Колебания в ДЛ
могут быть разложены на гармоничные
составляющие. При разноименных граничных
условиях с частотами
.
Таким образом, длинные линии обладают
колебательными свойствами. При этом
при разноименных граничных условиях в
ДЛ укладывается четверть волн, а при
одноименных - половина. Колебания в ДЛ
могут быть разложены на гармоничные
составляющие. При разноименных граничных
условиях с частотами
![]() ,
,
![]() ,
,
![]() и т.д. Поэтому ДЛ иногда называют
многоволновыми
колебательными системами.
и т.д. Поэтому ДЛ иногда называют
многоволновыми
колебательными системами.
В
рассмотренных случаях потери отсутствовали,
поэтому колебания являются незатухающими.
Если в линии существуют потери или
неполное отражение от конца или входа
линии (![]() и
и
![]() ),
то колебания будут затухающими.
),
то колебания будут затухающими.