4. Переходные процессы в цепях с сосредоточенными параметрами

4.1. Основные понятия и законы

В результате различных переключений в цепи, которые будем называть коммутациями, возникают переходные процессы.

Будем считать, что коммутация происходит мгновенно, а переходной процесс начинается с момента коммутации и длится теоретически бесконечно большое время. При этом момент времени непосредственно перед коммутацией обозначим , а сразу после нее .

Рассмотрим два закона коммутации.

Первый закон коммутации: В индуктивности в момент коммутации ток сохраняет значение, которое он имел непосредственно перед коммутацией, т.е.

Так, если до коммутации тока в катушке не было, то после коммутации он не может измениться скачком.

Второй закон коммутации: В момент коммутации напряжение на емкости сохраняется таким же, каким оно было до коммутации.

.

Первый и второй законы коммутации объясняются тем, что запасенная в индуктивности и емкости энергия не может измениться скачком, так как для этого потребовалась бы бесконечно большая мощность, которой реальные источники не обладают.

Рассмотрим понятия переходного, установившегося и свободного процессов на примере последовательной -цепи (рис.4.1). Для произвольного момента времени , где , где — ток переходного процесса.

Когда переходной процесс заканчивается, наступает принужденный режим, который создается ЭДС. Такой режим называется установившимся. Разность токов переходного и установившегося режимов называется свободным током . Тогда .

Таким образом, процесс в цепи можно условно считать состоящим из двух процессов, накладывающихся друг на друга (но это только удобный математический прием ).

В качестве начальных условий будем использовать значения токов и напряжений в момент

4.2. Переходные процессы в -цепи

А) Короткое замыкание -цепи

Пусть в схеме по рис.4.2.а произошла коммутация. Ток до коммутации

.

Поскольку установившийся ток в катушке равен нулю . Получаем:

.

Решение однородного дифференциального уравнения:

При этом ; .

Величину , имеющую размерность времени, назовем постоянной времени -цепи. Она соответствует времени, в течение которого ток уменьшается в раз в е раз (0.37). Графически это величина подкасательной.

Величина же обратная постоянной времени называется коэффициентом затухания. Свободный ток затухает тем медленнее, чем больше .

В момент коммутации значение тока поддерживается за счет ЭДС самоиндукции:

.

С энергетической точки зрения вся энергия, запасенная в катушке в течении переходного процесса превращается в тепло.

Постоянная времени обычно лежит в диапазоне от нескольких микросекунд до долей секунды.

Б) Включение -цепи на постоянное напряжение

По второму закону Кирхгофа для схемы по рис.4.3.а :

Получилось неоднородное дифференциальное уравнение, поэтому решение ищем в виде , где , тогда .

Для нахождения используем начальные условия : при . Следовательно, , (см. рис.4.3.б).

При этом энергия, получаемая от источника идет частично на увеличение энергии магнитного поля катушки, а частично переходит в тепло.

В) Включение -цепи на синусоидальное напряжение

Этот случай описывается тем же неоднородным дифференциальным уравнением, что и предыдущий, но тогда установившийся ток где , , .

При этом однородное дифференциальное уравнение остается без изменений, а следовательно переходный ток

Найдем . До коммутации тока не было, поэтому , , тогда .

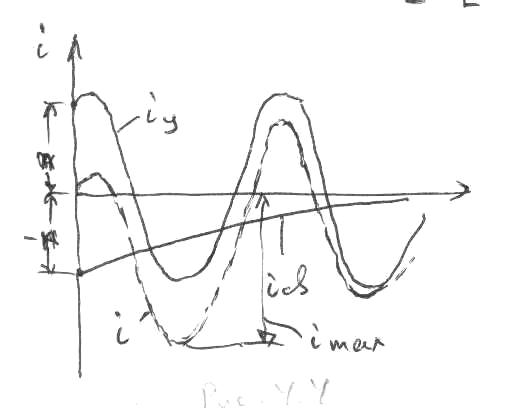
По мере затухания свободного тока переходной ток стремится к установившемуся (рис.4.4). При этом во время переходного процесса значение переходного тока может превышать амплитуду установившегося до двух раз (если ).

Рис. 4.4.

Если в начальный момент установившийся ток проходит через ноль то свободный ток не возникает вообще, так как его начальное значение также равно нулю.

Если в разветвленной цепи только одна индуктивность, то постоянная времени любого из токов одинакова и равна , где — входное сопротивление по отношению к выводам индуктивности, а — активное сопротивление обмотки.