39 Функция Кобба-Дугласа

Функция Кобба-Дугласа имеет вид:

.

При результат функционирования экономического объекта

.

К такому же выводу приходим и при , т.е. оба ресурса абсолютно необходимы.

Если K и L увеличить в λ раз, то в такое же количество раз возрастает и Y.

Действительно,

.

Эта функция находит широкое применение в моделях долгосрочного прогнозирования.

40 Средней производительности I-го ресурса

Пусть – ПФ. Дробь

называется средней производительностью i-го ресурса (фактора производства) (СПФ) или средним выпуском по i-му ресурсу (фактору производства).

41 Экономический смысл предельной производительности функции

Пусть – ПФ. Ее первая частная производная

называется предельной (маржинальной) производительностью i-го ресурса (фактора производства) (ППФ) или предельным выпуском по i-му ресурсу (фактору производства). Символика: .

Обозначим символами и ;

соответственно, приращение переменной и соответствующее ей частное приращение ПФ f(x). При малых имеем приближенное равенство

.

Следовательно, ППФ (приближенно) показывает, на сколько единиц увеличится объем выпуска у, если объем затрат i-го ресурса вырастает на одну (достаточно малую) единицу при неизменных объемах другого затрачиваемого ресурса. Здесь предельную величину (т.е. ППФ) целесообразно интерпретировать, используя близкое к ней отношение малых конечных величин, т.е. и . Отмеченное обстоятельство является ключевым для понимания экономического смысла ППФ . С другими предельными величинами следует поступать аналогичным образом.

42 ???????????????????

Задачи на экстремум имеют большое значение в экономике. Это вычисление, например, максимумов дохода, прибыли, минимума издержек в зависимости от нескольких переменных: ресурсов, производственных фондов и т.д. (примеры 26, 27).

Теория нахождения экстремумов функций нескольких переменных излагается в базовом курсе математики. Напомним основные моменты.

Частная производная функции по аргументу, например, х является обыкновенной производной функции одной переменной х при фиксированном значении у.

Точка , в которой для дифференцируемой функции выполняется условие (необходимое условие существования локального экстремума):

,

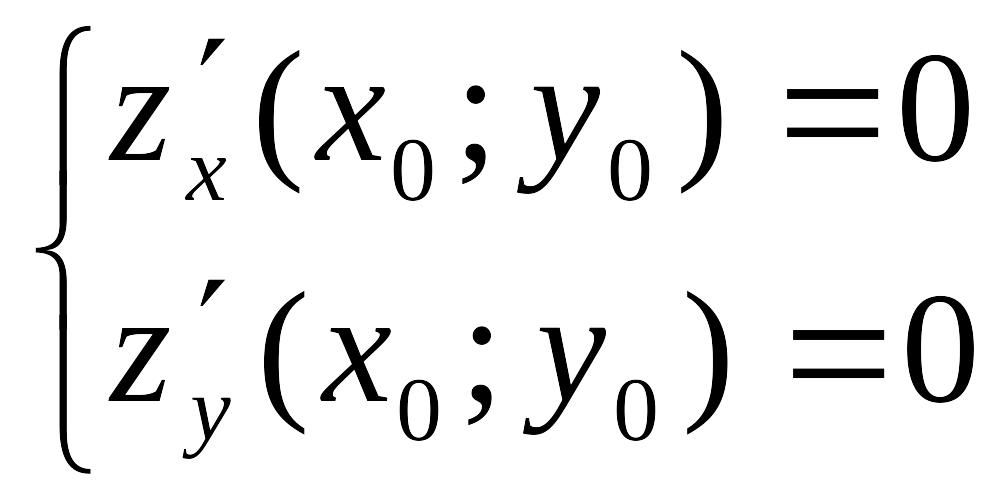называется критической точкой возможного экстремума или стационарной точкой.

Теорема (достаточное условие локального экстремума). Пусть в точке и в некоторой ее окрестности все вторые частные производные функции непрерывны. Тогда, если

,

то функция имеет в точке М₀ локальный экстремум: минимум при и максимум при . Если , то данная функция не имеет локального экстремума в точке М₀. Также дальше приводится задача на нахождение условного экстремума методом Лагранжа

43 ? Метод наименьших квадратов

Для множества точек наблюдений , можно попытаться выбрать различные типы кривых или прямую линию в зависимости от исходных данных. После подбора типа кривой можно проанализировать – какая кривая является «ближайшей» к точкам наблюдений. В качестве критерия «близости» используется минимум суммы квадратов разностей наблюдений зависимой переменной и теоретически подобранных значений , т.е. , где, .

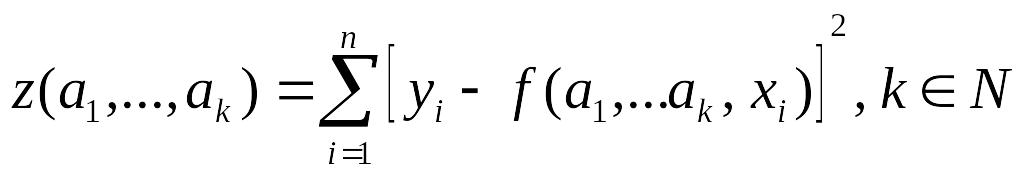Из теоремы дифференциального исчисления критическая точка на минимум находится из условий:

, .

P.S. Аналогичным образом можно выбрать наилучшую кривую по каждому типу кривой. Наиболее подходящим можно считать тот тип кривой, где будет наименьшее значение .

Наиболее часто используется функция вида , при график – прямая, при график – парабола и т.д. Иногда рассматриваются функции: , , , и т.д.