24 Принцип акселератора

Акселератор, ускоритель, в современной буржуазной макроэкономии коэффициент отношения прироста инвестиций к вызвавшему его относительному приросту дохода, потребительского спроса или готовой продукции. Акселератор (в экономике) выражается формулой (где I — инвестиции, Y — доход, t — время). Он служит количественным выражением «принципа акселерации», согласно которому каждый прирост или сокращение дохода, спроса или продукции вызывает (или требует) большего в относительном (процентном) выражении прироста или сокращения «индуцированных» инвестиций.

25 Определение эластичности

Определение. Предел отношения относительного приращения функции к соответствующему относительному приращению аргумента при условии, что абсолютное приращение аргумента стремится к нулю, называется эластичностью функции

26 Свойства эластичности

1. Эластичность – безразмерная величина, значение которой не зависит от того, в каких единицах измерены величины у и х. .

2. Эластичности взаимно обратных функций – взаимно обратные величины:

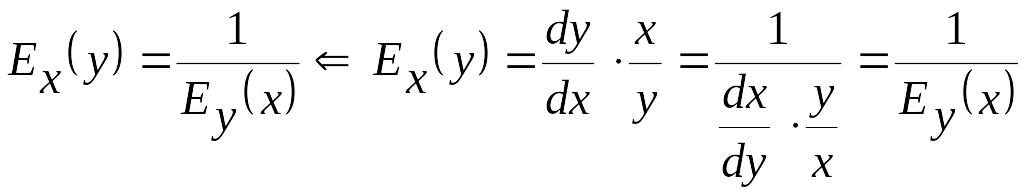Например, эластичность величины спроса по цене обратна эластичности цены по величине спроса

3. Эластичность произведения двух функций u(x) и v(x), зависящих от одного и того же аргумента х, равна сумме эластичностей:

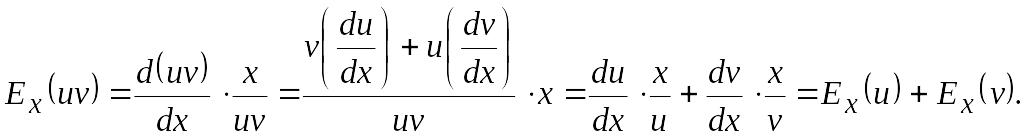4. Эластичность частного двух функций u(x) и v(x), зависящих от одного и того же аргумента х, равна разности эластичностей

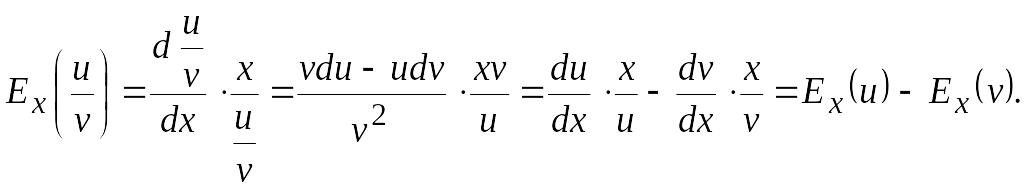
5. Эластичность суммы двух функций u(x) и v(x) может быть найдена по формуле:

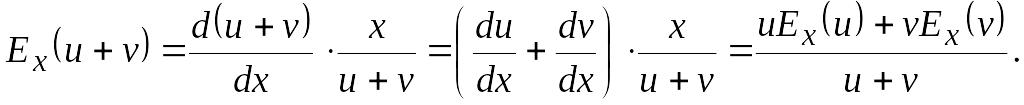
Например, эластичность величины спроса по цене обратна эластичности цены по величине спроса

3. Эластичность произведения двух функций u(x) и v(x), зависящих от одного и того же аргумента х, равна сумме эластичностей:

4. Эластичность частного двух функций u(x) и v(x), зависящих от одного и того же аргумента х, равна разности эластичностей

5. Эластичность суммы двух функций u(x) и v(x) может быть найдена по формуле:

27 эластичность элементарных функций

1. Эластичность степенной функции у=х^ постоянна и равна показателю степени : Е_х(х^) = .

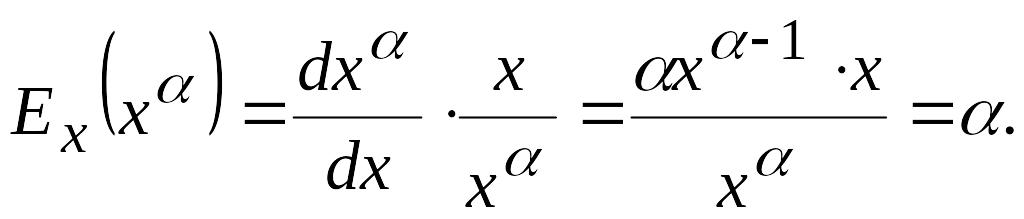
2. Эластичность показательной функции у=а^х пропорциональна х:

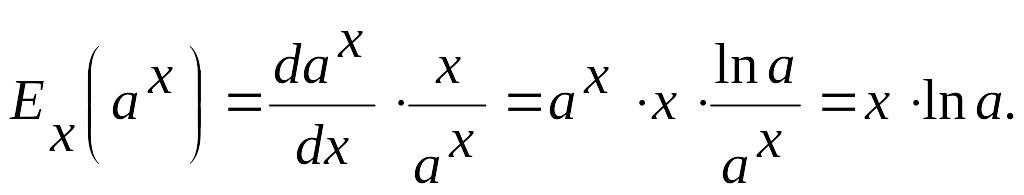
3. Эластичность линейной функции

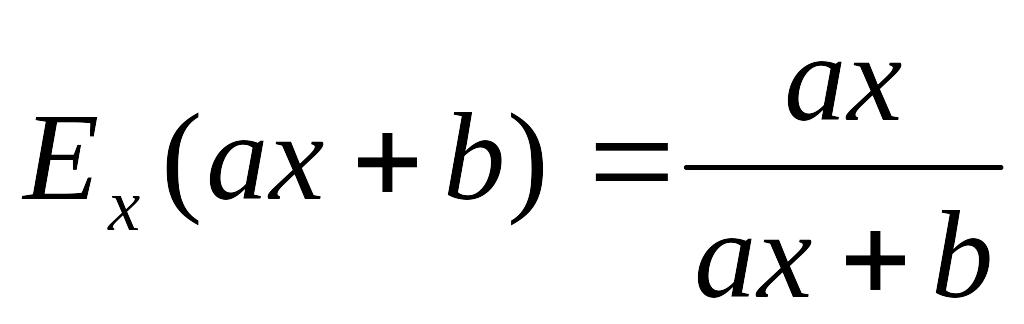
Если график линейной функции имеет отрицательный наклон (а<0), то эластичность функции меняется от нуля к точке y_m пересечения графиком оси у до минус бесконечности (-) в точке пересечения оси х, проходя через значение (-1) в средней точке.

28 Эластичность спроса по цене

1.Эластичность спроса по цене (прямая)

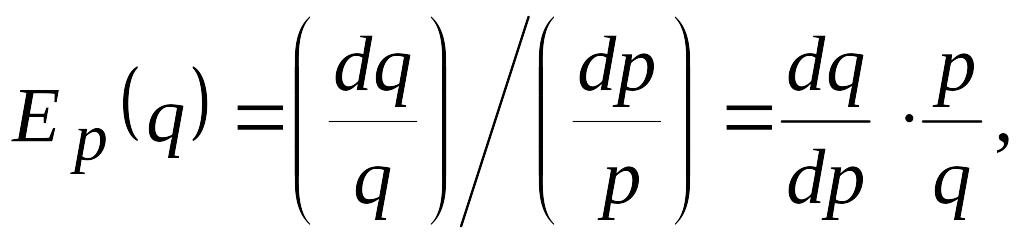
показывающая относительное изменение (выраженное в процентах) величины спроса на какое-либо благо при изменении цены этого блага на один процент и характеризующая чувствительность потребителей к изменению цен на продукцию. Если ценовая эластичность спроса по абсолютной

0

спрос

спрос

величине больше единицы, то спрос называют эластичным (совершенно эластичным при бесконечно большой величине эластичного спроса). Если ценовая эластичность спроса по абсолютной величине меньше единицы, то спрос называют неэластичным (совершенно неэластичным при нулевой эластичности спроса).

И, наконец, если ценовая эластичность спроса по абсолютной величине равна единице, то говорят о спросе с единичной эластичностью.