8. Теорема Больцано-Вейерштрасса
Каждая ограниченная последовательность имеет предельную точку. Из каждой ограниченной последовательности можно извлечь сходящуюся последовательность.
Вывод:
Пусть
-- последовательность действительных
чисел.
Т.к. она ограничена,
то найдутся такие числа m,
M,
что
.
Запишем алгоритм, по которому можно извлечь сходящуюся подпоследовательность. d=M-m – длина промежутка, где находится последовательность.
Алгоритм:
1. Начинаем построение подпоследовательности T(n).
,
где t1=1
2. Положим, что уже
выбрана последовательность
.
dn
– промежуток, который делит на 2 отрезка:
Выбираем левую половину, если в ней находится бесконечное число членов последовательности.
Т.о. в промежутке, который мы выбрали находится бесконечное число членов последовательности.
Выбираем эл-ов для подпоследовательности.
,
где
Длина промежутка:
Поэтому длина промежутка:
Т.о. d1, d2, …, dn получаем систему вложений => найдется точка принадлежащая всем отрезкам.
По построению T(1), T(2)…, T(n) – подпоследовательности.
Следовательно она сходится к конечному пределу.
9. Теорема о пределе монотонной последовательности. Число е
Монотонно возрастающая или убывающая последовательность всегда имеет конечный предел, т.е. сходится.
Вывод:
Предположим, что
последовательность ограничена снизу
и является монотонно убывающей, т.е.
найдется такое число m,
что
Нетрудно также
получить подпоследовательность
.
Смысл заключается в том, что из любой
ограниченной последовательности можно
извлечь сходящуюся подпоследовательность.
Остается показать, что это число является пределом последовательности.
Лемма о достаточном условии ограниченности последовательности.
Из сходимости последовательности следует ее ограниченность.
Вывод:
Пусть последовательность сходится, т.е. имеет конечный предел.
Тогда
.
Выберем окрестность точки А в радиусе
1.
Тогда найдется
такой номер k,
что для всех
.
Бесконечное число членов последовательности P(k), P(k+1) попадает в промежуток [A-1; A+1]. Но P(1)…P(k) могут не попасть в этот промежуток. Теперь нетрудно показать, что вся последовательность является ограниченной.
Число е.
Рассмотрим
последовательность
.
Эта последовательность является
возрастающей. Покажем, что она ограничена
сверху. Сделаем оценку для факториала.
В скобках получаем бесконечно убывающую геометрическую прогрессию:
при
всех
.
Мы показали
ограниченность последовательности
такая последовательность имеет предел,
который обозначается числом е.
.
Обозначение е введено Л. Эйлером.
10. Теорема о пределе суммы двух функций
Пусть
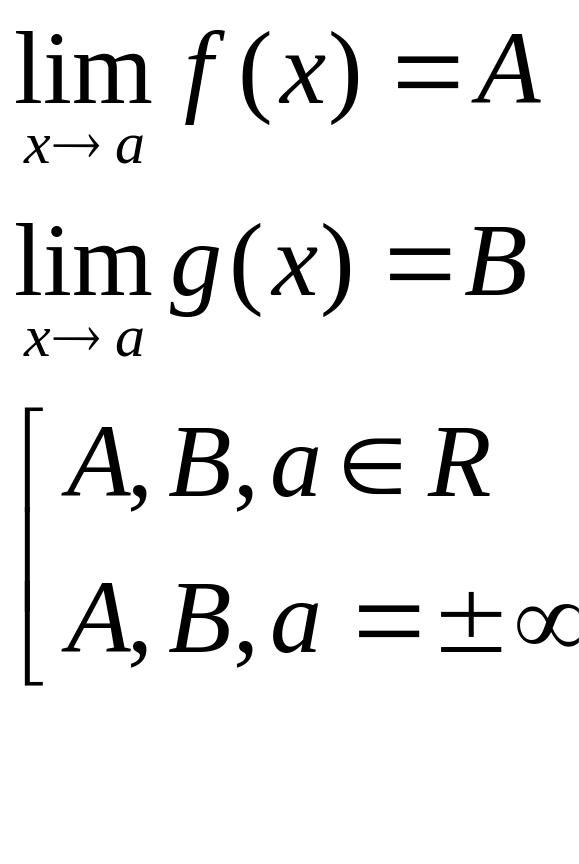
а –предельная
точка множества
c=const
Предел суммы функций равен сумме пределов.
Вывод:
Пусть
и существуют
конечные пределы
.
Выбираем произвольно
малые числа
.
Положим для определенности
.
Тогда найдется такая
-окрестность
точки а, что как только
Для всех
Выберем
таким малым, что
и
.
Тогда используем свойство неравенств,
получаем систему неравенств:
Нетрудно подобрать
настолько малым, что для выбранного
:
.
Т.к. мы выбрали произвольно, то согласно определению предела функции по Коши, мы доказали следующую теорему: