
- •1. Определение функции. Область определения и множество значений. Способы задания функции.
- •2. Определение последовательности, подпоследовательности и предельной точки последовательности. Ограниченные и монотонные, сходящиеся и расходящиеся последовательности.
- •3. Функция действительного переменного. Композиция функций. Понятие об элементарной функции.
- •4. Определение окрестности и предельной точки множества. Теорема о единственности предела функции.
- •5. Определение предела функции по Коши и по Гейне
- •7. Предел последовательности. Понятие о фундаментальной последовательности. Критерий сходимости Коши-Больцано(без вывода)
- •8. Теорема Больцано-Вейерштрасса
- •9. Теорема о пределе монотонной последовательности. Число е
- •10. Теорема о пределе суммы двух функций
- •11. Теорема о пределе произведения двух функций
- •12. Бесконечно малые и бесконечно большие функции. Основные свойства.
- •13. Эквивалентные функции. Теорема о замене эквивалентной функции под знаком предела
- •14. Непрерывность и разрывы функции в точке. Классификация разрывов
- •15. Свойства непрерывных функций в точке
- •16. Теорема об ограниченности непрерывной функции на замкнутом отрезке
- •17. Теорема о наибольшем и наименьшем значении непрерывной функции на замкнутом отрезке
- •18. Производная функции. Геометрический и механический смысл производной
- •19. Дифференциал функции. Теорема о дифференцируемости функции
- •20. Линейные свойства производной
- •22. Производная частного двух функций
- •23. Производная сложной функции. Инвариантность формы дифференциала
- •30. Теорема Лагранжа(теорема о конечных приращениях)
- •31. Теорема Коши(отношение приращения двух функций)
- •32. Правило Лопиталя(вычисление пределов)
- •33. Производные и дифференциалы высших порядков. Нарушение инвариантности формы дифференциала.
1. Определение функции. Область определения и множество значений. Способы задания функции.
Ф![]() ункция
– не пустое подмножество будем называть
функцией, если выполняется условие
однозначности.
ункция
– не пустое подмножество будем называть
функцией, если выполняется условие
однозначности.
![]()
для
![]()
П![]() олагаем:
олагаем:
y![]() =f(x)
=f(x)
Если A=D(f), то полагаем (f:A->B), т.е. А отображается в множество В.
Способы задания функции.
1. Аналитическое задание.
![]()
2. Графическое задание.
Очевидно, условие однозначности выполняется. Не всегда по графику можно найти аналитическую формулу.
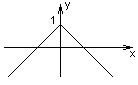
y=1-|x|
3. Табличное задание.
Русский алфавит можно рассматривать как пример табличного задания.
x: 1 2 3 4 5 6 … 33
y: а б в г д е … я
D(f)={1, 2, 3, …, 33}
E(f)={а, б, в, …, я}
2. Определение последовательности, подпоследовательности и предельной точки последовательности. Ограниченные и монотонные, сходящиеся и расходящиеся последовательности.
Отображение (Р: N->R) называется последовательностью действительных чисел.
Прим:
P(n)=1+(-1)n
P1=1-1
P2=1+1
(0; 2; 0; 2; …)
n! – n-факториал и n!=1*2*3*…*n
0!=1
1!=1
2!=2
3!=6
(n+1)!=(n+1)n!
Подпоследовательность числового ряда (1, 2, 3, …) определяется следующим образом.
(![]() S:
N->N)
S:
N->N)
Определение подпоследовательности для любой последовательности Р. Если S – последовательность натурального ряда, то P.S называют подпоследовательностью из последовательности Р.
Н![]() еформальный
выбор подпоследовательности из данной
последовательности:
еформальный
выбор подпоследовательности из данной
последовательности:
Чтобы выбрать подпоследовательность смещаемся вдоль последовательности слева направо и делаем выбор членов последовательности.
![]()
Выберем подпоследовательность, номера которой кратны 5:

3. Функция действительного переменного. Композиция функций. Понятие об элементарной функции.
Композиция функций.
Пусть А, В, С – множества(f: A-> B)(g: A -> C)
Тогда отображение h=gof называется композицией функций f и g.
h – сложная функция
![]() h(x)=g[f(x)]
h(x)=g[f(x)]
1. f(x)=3x-2 g(y)=y2
h(x)=gof(x)=(3x-2)2
2. h(x)=cos3(5x)
f1(x)=5x f2(x)=cosx f3(x)=x3
h=f3of2of1
Функция действительного переменного.
О![]()
![]() пр:
Отображение действительной функции
действительного переменного.
пр:
Отображение действительной функции
действительного переменного.
Примером являются все элементарные функции, которые образуются из основных элементарных функций с помощью операции композиции.
Основные элементарные функции:
1![]() .
Степенная
.
Степенная
2![]() .
Показательная
.
Показательная
3![]() .
Логарифмическая
.
Логарифмическая
4. Тригонометрическая
5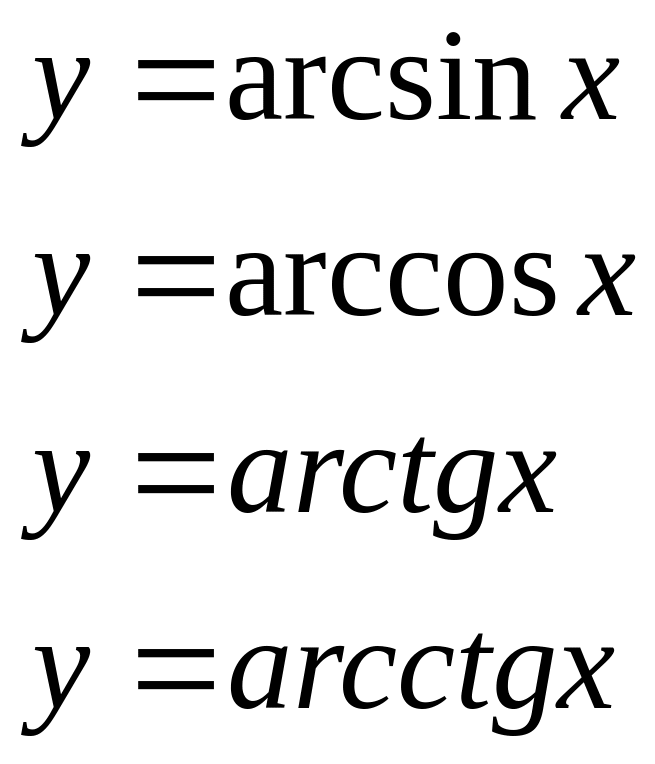 .
Обратные
.
Обратные
О пр.:
Пусть
1![]() .
f
ограничена сверху, если
.
f
ограничена сверху, если
2![]() .
f
ограничена снизу, если
.
f
ограничена снизу, если
3![]() .
f
ограниченная функция, если
.
f
ограниченная функция, если
4![]() .
f
монотонно возрастающая на подмножестве
, если
.
f
монотонно возрастающая на подмножестве
, если
![]()
5 . f монотонно убывающая на подмножестве ,если
![]()
6. Периодическая
функция, если найдется такое T>0,
что
![]() .
.
Т называют периодом – наименьшее положительное число Т обладающее этим свойством.
7. f
– четная, если
![]() .
.
8. f
– нечетная, если
![]() .
.
Область определения таких функций должна быть симметрична относительно точки х=0. Для четной функции симметрия относительно Оу.
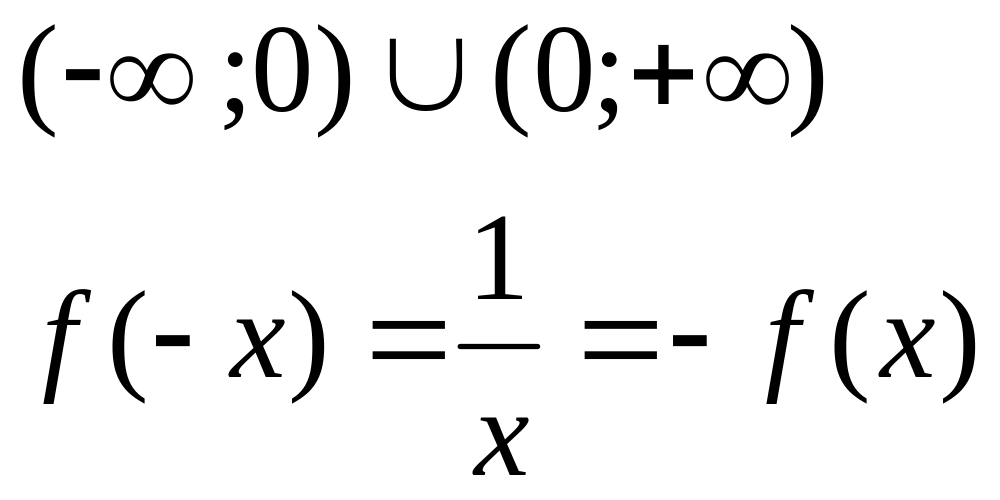
![]()
Симметрична относительно точки х=0. Функция является нечетной. График симметричен относительно начала координат.
D(f)=
![]()
E(f)=
y=arctgx
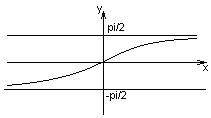
D(f)=
![]()
E(f)=
![]()
