30.Частные производные функции нескольких переменных.

Пусть дана ф-я Z=f(x;y), функция двух переменных, которая определена в некоторой ε окрестности точки (х₀; у₀)

▲х=х-х₀, ▲у= у-у₀ => для ¥ (х;у) € U_ε(х₀; у₀), (х;у)=( х₀ +▲х; у₀ + ▲у)

Рассмотрим ▲_хZ = f (х₀ + ▲х; у₀)- f (х₀ ;у₀) (частное приращение ф-ии Z по Х)

▲_уZ = f (х₀ ;у₀+▲у) - f (х₀ ;у₀) (частное приращение ф-ии Z по У)

Частной производной ф-ии Z=f(x;y) попеременной х в т. (х₀; у₀) наз-ся 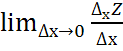, а по переменной у(х₀; у₀) называется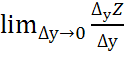

Обозначение

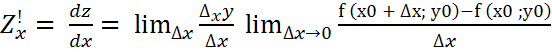
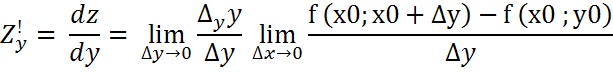
31. Дифференцируемость ф-и нескольких переменных

Определение. Функция f(x, y) дифференцируема в точке (x₀, y₀) (или сокращенно ), если справедливо равенство:

1. f(x, y)=f(x₀, y₀) + A(x - x₀) + B(y - y₀) + 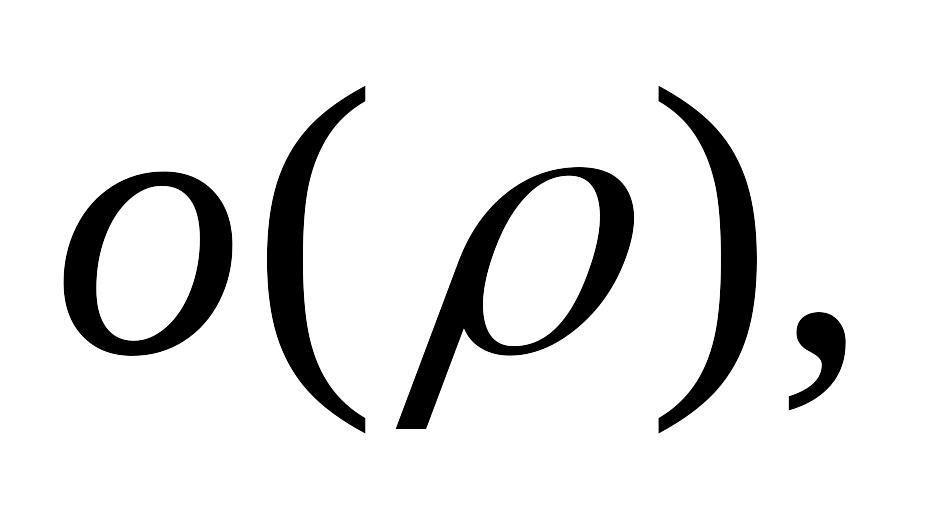где 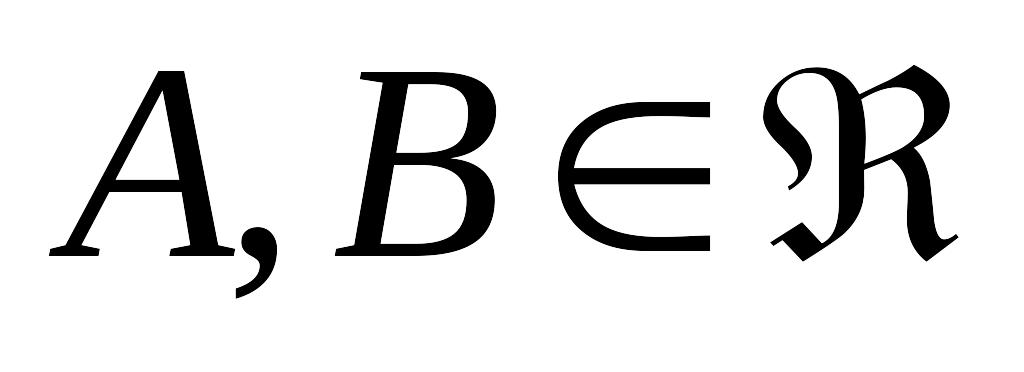- некоторые константы, а

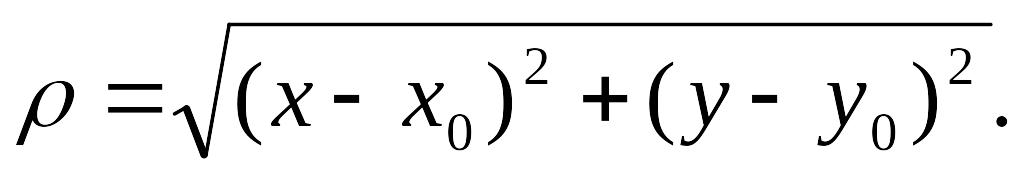
Зафиксируем одну из переменных, например: y=y₀. Тогда f(x₀, y₀) будет функцией от x и равенство (1) примет вид: f(x₀, y)=f(x₀, y₀) + A(x - x₀) + B(y - y₀) + o(x - x₀). Следовательно, число A есть производная функции f(x₀, y) в точке x=x₀. Эта производная обозначается так: и называется частной производной f(x, y) по x в точке (x₀, y₀). Аналогично: 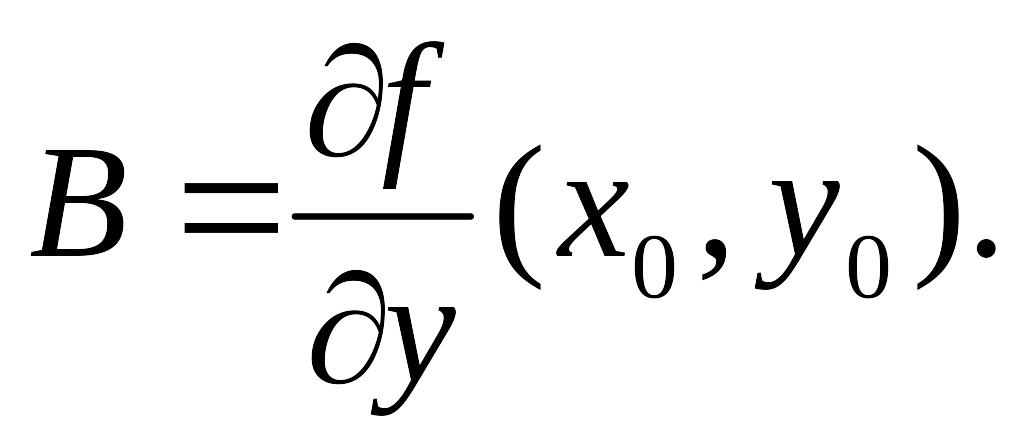Таким образом условие дифференцируемости функции f(x, y) в точке (x₀, y₀) можно представить в виде:

f(x, y)=f(x₀, y₀) ++ +

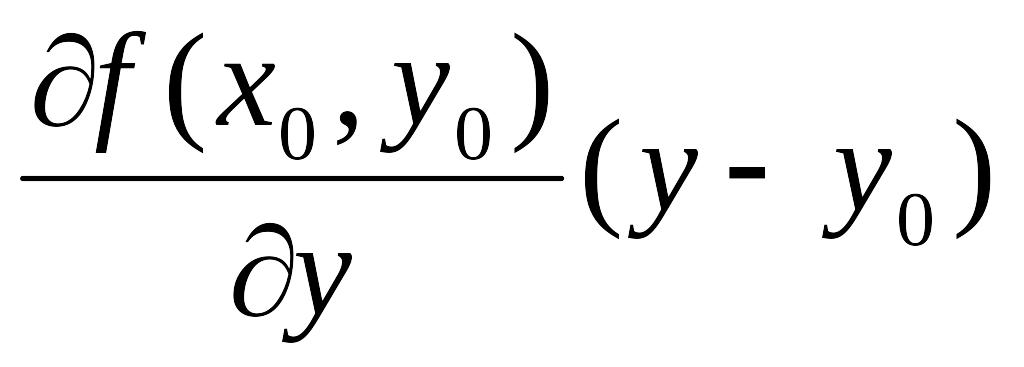Функция может быть дифференцируема по каждой из переменных в отдельности и при этом не быть дифференцируемой по совокупности переменных.

32. Дифференциал функции нескольких переменных.

Г лавная линейная относительно Δx и Δy часть полного приращения функции называется полным дифференциалом этой функции и обозначается dz или df(x,y) . Таким образом,

dz = Z^!_xdx + Z^!_Ydу полный дифференциал

33. Достаточное условие дифференцируемости ф-ии нескольких переменных.

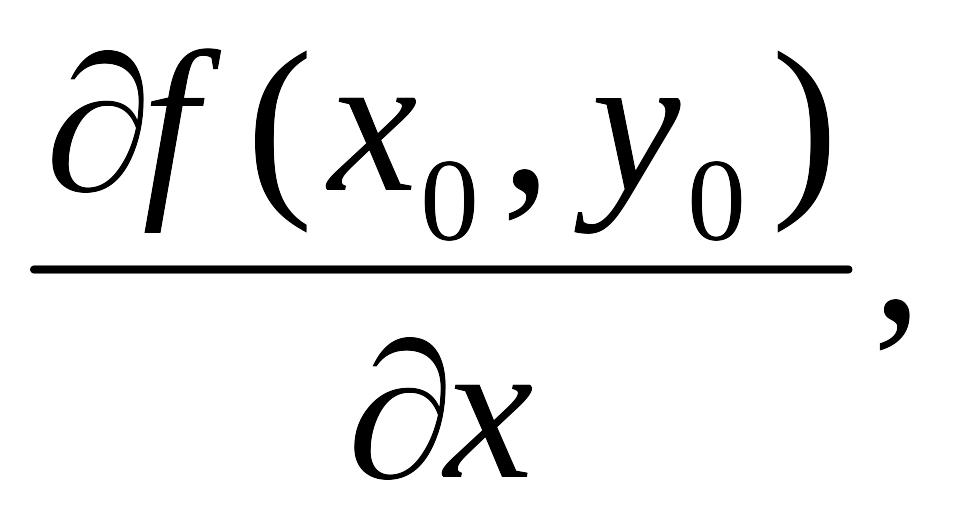
Теорема :Пусть функция f(x, y) определена в некоторой окрестности точки (x₀, y₀) и f(x, y), Тогда

34. Непрерывность дифференцируемой функции.

Если дифференцируема в точке (х₀; у₀) то Z= f(x) непрерывна в т. (х₀; у₀).

35.Однородные функции.

Функция у = f(X_l,x_1,..._,x_n) называется однородной степени а, если для любой точки (х₁,х_2, …x_n) из области определения D(f) и для любого положительного числа t точка (tx_l, tx_2,..._,tx_n) тоже принадлежит D(f), и справедливо равенство

f(tx_l,tx₂,..._,tx_n) = t^a*f(x_l,x_2,..._,x_n).

36. Формула Эйлера для однородной функции.

f 'x (х, у)х+ f 'y (х, у)y = a f (х, у)

37. Производная сложной функции.

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция также дифференцируема по x и ее производная равна

38. Производная по направлению.

Рассмотрим функцию от аргументов в окрестности точки . Для любого единичного вектора определим производную функции в точке по направлению следующим образом:

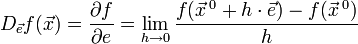
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора .

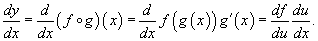
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!