
- •Числовые ряды.
- •Последовательность частичных сумм. Сумма ряда. Сходящиеся ряды.
- •Свойства сходящихся рядов
- •Необходимое условие сходимости числового ряда.
- •Числовые ряды с неотрицательными членами.
- •Критерий сходимости числовых рядов с неотрицательными членами.
- •Признаки сравнения, признак Даламбера и Коши, интегральный признак для числовых рядов с неотрицательными членами.
- •Знакопеременные ряды. Абсолютная и условная сходимость.
- •25. Функция нескольких переменных
- •26. Поверхности (линии) уровня функции нескольких переменных
- •29. Свойства функций, непрерывных на замкнутом ограниченном множестве: ограниченность, достижение наибольшего и наименьшего значения.
- •30.Частные производные функции нескольких переменных.
- •31. Дифференцируемость ф-и нескольких переменных
- •39. Градиент. Свойства градиента.
- •40.Частные производные высших порядков.
- •41. Теорема о равенстве смешанных производных.
- •42. Формула Тейлора для функции нескольких переменных с остаточным членом в формуле Лагранжа.
- •43. Локальные экстремумы функций нескольких переменных.
- •48. Наибольшее и наименьшее значение непрерывной функции на замкнутом ограниченном множестве.
- •Оглавление
25. Функция нескольких переменных
Функции нескольких переменных
У = f (х1,х2,... ,хп) используются для описания тех встречающихся в практических задачах ситуаций, когда значение одной величины у однозначно определяется значениями набора величин х1, х2,...,хп. Иногда вместо y = f(xl,x2,...,xn) пишут у = f(А), где A = (x1,x2,...,xn) ϵ Rn.
Величины х1, х2,...,хп называются аргументами функции; множество допустимых значений аргументов А = ( х1, х2,..., хп) называется областью определения функции и обозначается D(f). Множество значений у= f(A), получающихся при всех А из области определения, называется областью значений функции.
26. Поверхности (линии) уровня функции нескольких переменных
линии (поверхности) уровня. Для непрерывной функции двух переменных у = f(x1, х2) линии уровня - это линии на плоскости с координатами (х1, х2), задаваемые уравнениями f{x1, x2)=ck для некоторого набора значений функции с1,с2, ...,ст. Например, горизонтали на топографической карте являются пиниями уровня для функции высоты над уровнем моря. При п > 2 говорят о поверхностях уровня.
Скалярное поле можно представить графически с помощью поверхности уровня (также называемой изоповерхностью). Поверхностью уровня скалярного поля u = u(x,y,z) называется множество точек пространства, в которых функция u принимает одно и то же значение c, то есть поверхность уровня определяется уравнением u(x,y,z) = c.
Для плоского поля вместо поверхности получаются линии уровня. Примеры: изобата, изотерма и прочие изолинии.
27-28. Предел и непрерывность функции нескольких переменных
Пусть
дана функция у
=
f(А),
и
пусть D(f)
- область ее определения. Предположим,
что точка А0
является
предельной точкой множества D(f).
Рассмотрим все сходящиеся к А0
последовательности
точек множества
D(f),
ни один из элементов которых не совпадает
с точкой А0.
Для
каждой
такой последовательности {Ак}
построим
последовательность значений {fk}:
fk=
f(Ak).
Если
окажется, что все построенные так
последовательности значений функции
сходятся к одному, общему для них всех,
числу а,
то это число называется пределом
функции y
=
f(A)
в точке A0
и
обозначается ![]() .
.
Функция у = f(A) называется непрерывной в точке А0 ϵ D(f) , если предел существует и равен f(А0). Функция у = f(А) называется непрерывной на множестве М, если она непрерывна в каждой точке этого множества.
29. Свойства функций, непрерывных на замкнутом ограниченном множестве: ограниченность, достижение наибольшего и наименьшего значения.
1) Если– непрерывна на замкнутом и ограниченном множестве, то она ограничена на этом множестве и принимает на этом множестве своё наибольшее и наименьшее значение. 2) Если z=f (x1, x2,.., xn) непрерывна в некотором множестве Х и в некоторых его точках принимает значение в точках А и В, А<В, то для любой точки С: А<С<В найдется Х – точка с коэффициентом = (x1, x2,.., xn) € Х такая что : f(x)=C.
3) Если f(x) и g(x) непрерывна в точке х=х0, то f(x) ± g(x), f(x) * g(x), f(x) ÷ g(x), где g(x) ≠ 0 непрерывна в точке х=х0.
4) Если f(x) непрерывна в точке х0, а ϕ(t)- это функция одной переменной определена и непрерывна в т. t0 = f(x0) => ϕ (f(x)) непрерывна в точке t0 = f(x0) => а значит в точке х0.
(об
ограниченности и существовании
экстремумов) Если
функция
![]() непрерывна
в замкнутой и ограниченной области
непрерывна
в замкнутой и ограниченной области
![]() ,
то:
,
то:
1)
функция
ограничена
на
,
то есть существует такая постоянная
![]() ,
что
,
что
![]() при
всех
при
всех
![]() ;
;
2)
функция
принимает
в области
![]() наибольшее
и наименьшее значения, то есть существуют
такие точки
наибольшее
и наименьшее значения, то есть существуют
такие точки
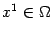 и
и
![]() ,
что при всех
выполняются
неравенства
,
что при всех
выполняются
неравенства
![]() и
и
![]() .
.
(В
этом случае точка
![]() называется
точкой
минимума,
а точка
называется
точкой
минимума,
а точка
![]() -
точкой
максимума
функции
в
области
.)
-
точкой
максимума
функции
в
области
.)
