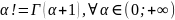31.Эйлеров интеграл первого рода. Бета-функции.

Определение 1. Интеграл 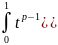по предложению Лежандра называется эйлеровым интегралом первого рода.

Вещестевнные параметры p,q входящие в задание интеграла (1) определяют свойство этого интеграла

При p,q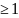 подинтегральная функция непрерывна на [о,1] а значит (1) – определенный зависящий от параметров p и q интеграл.

Если p<1,q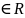 то подинтегральная функция неопределена в левом конце отрезка [0,1], т.е. t=0 причем подинтегральная функция при t →+0 неограничена, возрастает

Если q<1, то подинтегральная функция неопределена в левом конце отрезка [0,1], т.е. t=1 причем подинтегральная функция при t →1-0 неограничена, возрастает.

Ф-ию В с множеством определения DB= {(p,q):p>0,q>0}, заданную с помощью эйлерового интеграла 1 рода

В: (p,q) →

Назовем бета-функцией.

Теорема.

Бета – функция непрерывна на всем множестве определения

32.Эйлеров интеграл второго рода. Гамма-функции.

Определение 1. Интеграл по предложению Лежандра называется эйлеровым интегралом второго рода.

Параметр p входящий в задание интеграла (1) определяют свойство этого интеграла

Интеграл (1) является нествобственным.

Ф-ию Г с множеством определения DB= (0;+∞), заданную с помощью эйлерового интеграла 2 рода

Г: (p,q) →

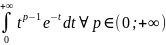
Назовем гамма-функцией.

Теорема.

Гамма – функция непрерывна на ее множестве определения

33.Формулы приведения бета-функции

Свойство 1.

Для бета-функции имеют место формулы приведения:

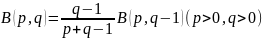(1)

И

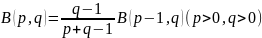(2)

Свойство 2

Для бета-функции имеют место формулы:

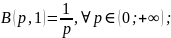(3)

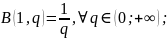(4)

B(1,1)=1 (5)

Свойство 3. Имеет место формула

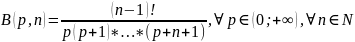(6)

Доказательство. Последовательно применяя (1) при натуральном n находим:

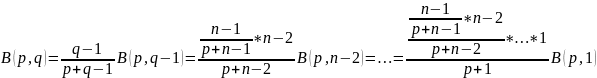
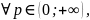
Отсюда с учетом формулы (3) получаем формулу (6)

Если Кроме q=n параметр p есть натуральное число, то из (6) получаем:

Формула дополнения бета-функции

Лемма 1. Пусть натуральные числа m,n такие, что m<n. Тогда имеет место формула

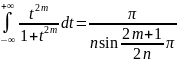
Свойство 1. При 0<a<1 имеет место формула дополнения

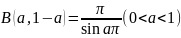
34. Дифференцирование гамма-функции.

Определения 1. Функцию Г с множеством определения DГ = (0;+∞) заданную с помощью эйлерова интеграла второго рода

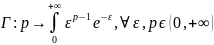
Назовем гамма-функцией

Теорема 1. Гамма функция непрерывна на ее множестве определения.

Теорема 2. Гамма функция бесконечное число раз непрерывно дифференцируема на множестве определения, а ее производная l-го порядка находится по формуле:

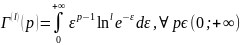
35.Формула приведения гамма - функции

Свойство 1. Для гамма – функции имеет место формула приведения

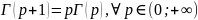
Доказательство. Положим

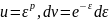
Тогда при p>0 находим

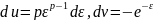
Интегрированием по частям устанавливаем, что

□

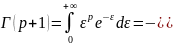Повтороне применение формулы приведения (1) дает формулу

Г(p+n)=(p+n-1)(p+n-2)*…*(p+1)pГ(p),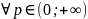 , 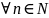(2)

Формула (2) позволяет свести вычисление гамма-функции для сколь угодного большого значения аргумента к вычислению гамма-функции от аргумента, меньшего единицы.

Поскольку

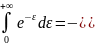
То Г(1)=1

Г(n+1)=n!,

Поэтому гамма-функция является обобщением факториала. С помощью гамма – функций понятие факториала можно расспространить на множество положительных вещественных чисел, приянв по определению, что