23. Связь между поверхностными интегралами первого и второго родов

Пусть поверхность S задана уравнение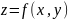м: , причем , 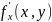, 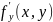– непрерывные функции в замкнутой области T (проекции поверхности S на координатную плоскость 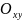, а функция 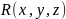непрерывна на поверхности S.

Нормаль к поверхности S, имеющая направляющие косинусы 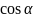, , 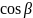, 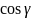выбрана к верхней стороне поверхности S. Тогда

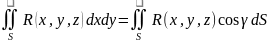
Для общего случая имеем:

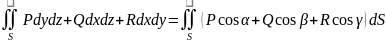
24. Формула Остроградского-Гаусса

Теорема. Если функция P(x,y,x), Q(x,y,z),R(x,y,z) непрерывно дифференцируемы в обьемно односвязной области G то для любой простой замкнутой области V<G ограниченой кучочно гладкой поверхностью Ф верна формула Остроградского – Гаусса:

Где поверхностный интеграл второго рода вычисляется по внешней стороне поверхности Ф.

Формулу Остроградского – Гаусса можно также записать в виде

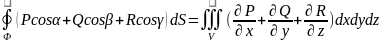
Где cos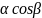 cos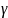 – напрявляющие косинусы единичного вектора внешней нормали к поверхности Ф.

25. Формула Стокса

Пусть гладкая двусторонняя поверхность Ф ограниченная гладким контуром L задана параметричекски уравнениями

(u;v)

С помощью функций x (u,v),y(u,v),z(u,v) дважды непрерывно дифференцируемых в замкнутой области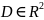 ограниченной гладким контуром L*

Контуру L* при отображении определяемом функциями x (u,v),y(u,v),z(u,v) соответствует контур L ограничивающий поверхность Ф. Обходу контура L* на плоскости отвечает обход контура L и наоборот. Условимся считать положительными такое направление обхода контура L которому соответствует положительное направление обхода контура L*. Если единичный вектор n нормали к поверхности определить формулой

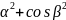cos + cos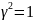 то при положительном обходе контура L поверхность будет оставаться слева если смотреть с конца вектора n. Таким образом положительное направление обхода границы поверхности согласуется с выбором ее стороны.

cos cos – направляющие косинусы вектора n в произвольной точке М поверхности Ф

Пусть в некоторой пространсвтенной области G целиком содержащей поверхность Ф, заданы непрерывно дифференцируемые функции P(x,y,z), Q(x,y,z),R(x,y,z). Тогда имеет место формула Стокса:

Где обход контура L при выбраной стороне поверхности Ф происходит в положительном направлении.

Эту формулу используя поверхностный интеграл второго рода можно записать следующим образом

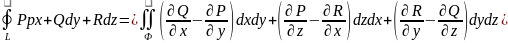
26. Сходимость функции двух переменных

Определение 1. Функция f(x,y)→ f(x,y) c Df=G сходится в точке x=x₁ из множества G_x при y→ y₀ если функция переменной

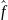: y →f (x₁,y), 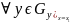, сходится при y→ y₀. А предел

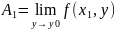
Назовем пределом функции f в точке x= x₁ при y→ y₀

Определение 2. Сужение функции двух переменных

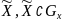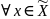f:(x,y) → f(x,y), Df=G равномерно сходится на множестве , к функции А: x → A(x), , при y→ y₀ если для любого положительного числа существует такое положительное число зависящее от что при всех y из множества для которых

0<| y- y₀ |< выполняет неравенство |f(x,y)-A(x)|< для всех x из множества .

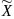Критерий Гейне равномерной сходимости. Для того чтобы сужение функции двух переменных f:(x,y) → f(x,y), Df=G равномерно сходилось на множестве , к функции А: x → A(x), , при y→ y₀ необходимо и достаточно, чтобы для любой числовой последовательности 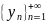состоящей из элементов 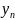множества , и стремящейся к 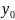, соответствующая функциональная последовательность 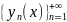с членами 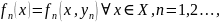равномерно сходилась на множестве .

M-Критерий равномерной сходимости функции двух переменных к предельной функции. Для того чтобы сужение функции двух переменных f:(x,y) → f(x,y), Df=G равномерно сходилось на множестве , к функции А: x → A(x), , при y→ y₀ необходимо и достаточно, чтобы для любого положительного числа существовало такое положительное число зависящее от что при всех y из множества для которых 0<| y- y₀ |< выполняет неравенство |f(x,y)-A(x)|< 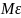для всех x из множества , где положительно число М не зависит ни от х ни от у ни от

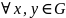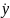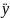Критерий коши равномерной сходимости функции двух переменных. Для того чтобы сужение функции двух переменных f:(x,y) → f(x,y) ), имело предельную функцию при y→ y₀ и сходилось к ней равномерно на множестве , необходимо и достаточно, чтобы для любого >0 существовало такое положительное число зависящее от , что при любых из множества таких что 0<| - y₀ |< , 0<| - y₀ |< , выполнялось неравенство |f (x, )- f(x, )|< для всех x из множества .