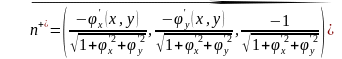- •1) Кусочно-гладкие кривые. Способы задания кривых.
- •2)Криволинейные интегралы первого рода
- •3)Механический, экономический и геометрический смыслы криволинейного интеграла первого рода.
- •4)Вычисление кри-1 с помощью определенного интеграла.
- •5. Криволинейные интегралы второго рода
- •6. Связь между кри 1-ого и 2-ого рода
- •7. Вычисление кри-2 с помощью опред. Инт.
- •8. Формула Грина
- •9. Условия независимости криволинейного интеграла 2 рода от пути интегрирования.
- •10. Восстановление ф-ции по её полному дифференциалу.
- •11. Множества, измеримые по Жордану
- •12. Определение кратного интеграла
- •13. Вычисление двойного интеграла по прямоугольнику.
- •14. Вычисление двойного интеграла по компакту.
- •17. Замена переменных в двойных интегралах
- •18. Замена переменных в кратном интеграле
- •19. Кратные несобственные интегралы
- •20. Понятие поверхностных интегралов первого и второго рода
- •21.Существования поверхностноо интеграла 1го рода
- •22. Существование поверхностного интеграла второго рода
- •23. Связь между поверхностными интегралами первого и второго родов
- •24. Формула Остроградского-Гаусса
- •25. Формула Стокса
- •26. Сходимость функции двух переменных
- •27. Понятие определенного интеграла, зависящего от параметра
- •28. Предел, непрерывность, дифференцирование, интегрирование функций, заданных оизоп
- •29. Понятие несобственного интеграла, зависящего от параметра
- •30. Сходимости несобственного интеграла, зависящего от параметра
- •31.Эйлеров интеграл первого рода. Бета-функции.
- •32.Эйлеров интеграл второго рода. Гамма-функции.
- •33.Формулы приведения бета-функции
- •34. Дифференцирование гамма-функции.
- •35.Формула приведения гамма - функции
- •36.Формула связи между бета и гамма функциями
- •37. Определение интеграла Фурье
- •38. Сходимость интеграла Фурье в точке
- •39. Прямое и обратное преобразования Фурье
- •40. Косинус- и синус- преобразования Фурье
20. Понятие поверхностных интегралов первого и второго рода
Первого рода
Пусть Ф —
гладкая, ограниченная полная поверхность.
Пусть
далее на Ф задана
функция
f(M)=f(x,y,z).
Рассмотрим
разбиение T этой
поверхности на части
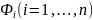 кусочно-гладкими
кривыми и на каждой такой части выберем
произвольную точку
кусочно-гладкими
кривыми и на каждой такой части выберем
произвольную точку 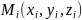 .
Вычислив
значение функции в этой точке
.
Вычислив
значение функции в этой точке
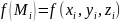 и,
приняв за
и,
приняв за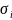 — площадь поверхности
— площадь поверхности 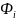 рассмотрим
сумму
рассмотрим
сумму 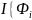 ,
,
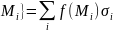
Тогда
число I называется
пределом сумм
,
 ,
если:
,
если:
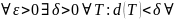 {
{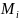 }|
,
}|
,
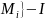 |<
|<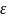
Предел 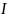 сумм
,
при
d(T)->0 называется
поверхностным интегралом первого рода
от функции f(M) по
поверхности Ф и
обозначается следующим образом:
сумм
,
при
d(T)->0 называется
поверхностным интегралом первого рода
от функции f(M) по
поверхности Ф и
обозначается следующим образом:
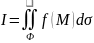
Второго рода
Рассмотрим двустороннюю
поверхность ![]() ,
гладкую или кусочно-гладкую, и фиксируем
какую-либо из двух ее сторон, что
равносильно выбору на поверхности
определенной ориентации.
,
гладкую или кусочно-гладкую, и фиксируем
какую-либо из двух ее сторон, что
равносильно выбору на поверхности
определенной ориентации.
Для определенности предположим сначала, что поверхность задана явным уравнением Z=Z(x,y) причем точка (x,y) изменяется в области (D) на плоскости x,y, ограниченный кусочно-гладким контуром.
Пусть
теперь в точках данной поверхности Ф определена
некоторая функция f(M)=f(x,y,z).
Разбив поверхность сетью кусочно-гладких
кривых на части
и
выбрав на каждой такой части
точку
вычисляем
значение функции
в
данной точке и умножим его на
площадь  проекции
на плоскость x,yэлемента
,
снабженную определенным знаком. Составим
интегральную сумму:
проекции
на плоскость x,yэлемента
,
снабженную определенным знаком. Составим
интегральную сумму:
.
Конечный предел этой интегральной суммы при стремлении диаметров всех частей к нулю называют поверхностным интегралом второго рода от
, f(M)dxdy=f(x,y,z) dxdy
распространенным на выбранную сторону поверхности , и обозначают символом
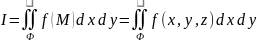
(здесь dxdy) напоминает о площади проекции элемента поверхности на плоскость xy
Если вместо плоскости xy спроектировать элементы поверхности на плоскость yz или zx, то получим два других поверхностных интеграла второго типа:
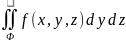 или
или 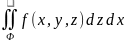 .
.
В приложениях чаще всего встречаются соединения интегралов всех этих видов:

где P,Q,R суть функции от (x,y,z), определенные в точках поверхности Ф.
21.Существования поверхностноо интеграла 1го рода
Введем функции
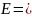 (1)
(1)
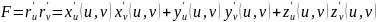 (2)
(2)
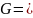 (3)
(3)
Теорема. Пусть Ф – гладкая поверхность не имеющая особых точек и заданная параметрически уравнениями
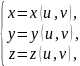 (u;v)
(u;v)
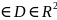
И
пусть функция f(m)=f(x,y,z)
непрерывна во всех точках М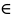 Ф
включая край поверхности Ф. Тогда
поверхностный интеграл первого рода
:
Ф
включая край поверхности Ф. Тогда
поверхностный интеграл первого рода
: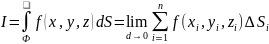 (4)
(4)
Существует и может быть вычислен по формуле
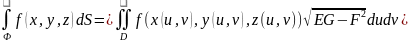 (5)
(5)
Где функции F,G,E переменных u и v определены соотношениями (1)-(3)
В случае поверхности Ф, заданной явно уравнением z=f(x,y) формула (5) принимает вид:
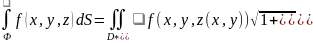
Где D*- проекция поверхности Ф на плоскость хОу.
22. Существование поверхностного интеграла второго рода
Теорема.
Пусть S={r(u,v)|(u,v)
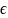 Ω}
– элементарная гладкая поверхность, Ω
- открытое измеримое по Жордану множество
в R2.
Пусть P,Q
, R:
Ω}
– элементарная гладкая поверхность, Ω
- открытое измеримое по Жордану множество
в R2.
Пусть P,Q
, R: причем
причем
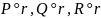 – непрерывные функции на
– непрерывные функции на
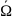 .
Тогда полный поверхностный интеграл
второго рода от ф-ий Q,P,R
по выбраной стороне поверхности S
существует и вычисляется по формуле
.
Тогда полный поверхностный интеграл
второго рода от ф-ий Q,P,R
по выбраной стороне поверхности S
существует и вычисляется по формуле
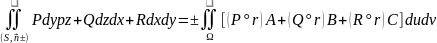
Следствие.
Если
поверхность S
имеет явное задание z
=
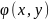 ,
где
– непрерывно дифференцируемая в
измеримой области D
функция P,Q
, R:
причем
P(x,y,
),
Q(x,y,
),
R(x,y,
)
– непрерывные на
,
где
– непрерывно дифференцируемая в
измеримой области D
функция P,Q
, R:
причем
P(x,y,
),
Q(x,y,
),
R(x,y,
)
– непрерывные на
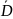 функции, то полный поверхностный интеграл
по выбраной стороне поверхности
функции, то полный поверхностный интеграл
по выбраной стороне поверхности
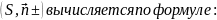
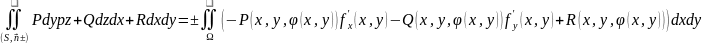
Доказательство. Для доказательства достаточно учесть что верхняя сторона поверхности соответствует единичной нормали, образующему с осью OZ острый угол, то есть