13. Вычисление двойного интеграла по прямоугольнику.

Теорема. Если существует двойной интеграл от функции 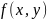по прямоугольнику D и при каждом фиксированном значении 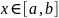существует определенный интеграл

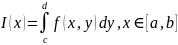
То существует повторный интеграл

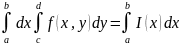
Причем двойной интеграл равен повторному ,

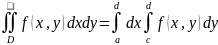
14. Вычисление двойного интеграла по компакту.

Определение. Область интегрирования D называется правильной в направлении координатной оси Оу, если ее можно задать в виде

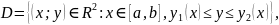
Где функци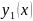и и 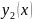непрерывны на отрезке 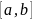и удовлетворяют неравенству

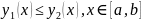. Аналогично вводится понятие области, правильной в направлении координатной оси Ox.

Теорема. Если существует двойной интеграл от функции по области интегрирования D и при каждом фиксированном 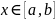существует интеграл

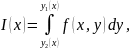
То существует повторный интеграл

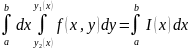
Причем верно равенство

.

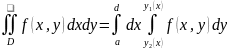17. Замена переменных в двойных интегралах

Замена переменных в двойном интеграле описывается формулой

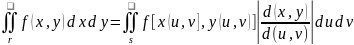
где выражение 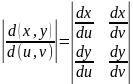  ≠0 представляет собой так называемый якобиан преобразования (x,y)->(u,v), а S − образ области интегрирования R, который можно найти с помощью подстановки x=x(u,v), y=y(u,v) в определение области R. Отметим, что в приведенной выше формуле 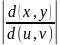 означает абсолютное значение соответствующего определителя.  Предполагая, что преобразование координат  (x,y)->(u,v) является взаимно-однозначным, обратное соотношение описывается якобианом

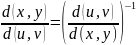
при условии, что знаменатель нигде не равен 0.  Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:

1. Найти образ S в новой системе координат (u,v) для исходной области интегрирования R;

2. Вычислить якобиан преобразования (x,y)->(u,v) и записать дифференциал в новых 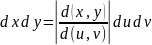переменных;

3. Заменить в подынтегральном выражении исходные переменные x и y, выполнив, соответственно, подстановки x=x(u,v),и y=y(u,v) 

18. Замена переменных в кратном интеграле

Предположим, что G - ограниченная измеримая область в R_n , отображение F:G--> R_n  взаимно однозначно и непрерывно дифференцируемо, область G' =F(G) измерима. Пусть отображение F задается при помощи непрерывно дифференцируемых функций

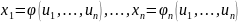
Обозначим определитель матрицы частных производных этих функций – якобиан отображения F - через  J(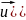

J(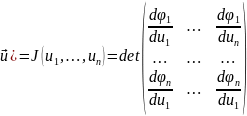

Кроме того предположим, что функция f ( 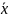  ) = f (x₁ , . . . , x_n) непрерывна на 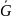- замыкании области G.

Тогда справедлива формула замены переменных в кратном интеграле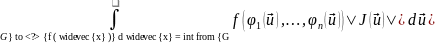

19. Кратные несобственные интегралы

Пусть G – область в 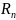, функция , интеграл не существует из-за того, что либо область G не ограничена, либо функция f не ограничена в области G, либо и то, и другое, но на каждом замкнутом кубируемом подмножестве функция f интегрируема по Риману. При выполнении всех перечисленных выше условий будем называть несобственным кратным интегралом