1) Кусочно-гладкие кривые. Способы задания кривых.

Опр. Если кривая L с началом в т. А и концом в т. В, с параметр. заданием L={(x,y):х=x(t), y=y(t), t [α,β]} (1) так что А(x(α), y(α)), B(x(β), y(β)) ф-ции х: [α,β] →R, y:[α,β] →R непрерывно дифер. на смежных отрезках [t_i,t_i+1], α=t₀ β=t_n причём сумма квадратов производных (Dx(t))²+(Dy(t))²≠0 t [α,β], то эта ф-ция наз. кусочно-гладкой.

Параметрическое задание простр. кривой: L={(x,y,z):х=x(t), y=y(t), z=z(t), t [α,β]} (2) наряду с задание (1) исп. запись: L={X_t:X_t(x(t),y(t),z(t)) (3) t [α,β]}, где А=X_α , B=X_β

Зад. rр. L, в случае когда в качестве параметра выступает длина пути: L={(x,y,z):х=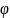 (s), y= (s), z= (s), s [0,e]} (4)

(1) и (2) наз. параметрическим заданиями кривой L, а запись (3) наз. естественной параметризацией кривой L, s называют натуральным параметром.

2)Криволинейные интегралы первого рода

Пусть V C R³, ф-ция f: V→R . Возьмём кусочно-гладкий контур L C V заданный естественной параметризацией: L={(x,y,z):х= (s), y= (s), z= (s), s [0,e]} , выполним разбиение отрезка [0,e] на смежные отрезки: [0,e] = _k , S_k+1], S₀=0, S_n=e тогда весь путь L будет разбит точками X_k( (S_k), (S_k), (S_k)) на смежные участки = L X_k( (S_k), (S_k), (S_k)) составит сумму б= *∆S_k где x_k= (S_k), y_k= (S_k), z_k= (S_k), ∆S_k=| x_k x_k+1| которая называется интегральной суммой ф-ции f вдоль пути L соотв. разбиению .

Опр. Если интегральные суммы ф-ции f вдоль пути L при б имеет предел =I, то этот предел наз. Криволинейным интегралом первого рода от ф-ции f вдоль пути L и обозн. ^{L L}

3)Механический, экономический и геометрический смыслы криволинейного интеграла первого рода.

Механический смысл:

Опр1. Материальное тело объёмной характеристикой которого является длина называется материальной нитью. Пусть непрерывная вдоль мат. нити ф-ция 3-х переменных задаёт плотность распределения массы в каждой точке (x,y,z) L, выполним разбиение этой нити на участки L= , выбрав достаточно малый диаметр разбиения ,ввиду непрерывности ф-ции 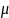можем утверждать, что масса нити m_L= 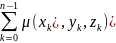∆_k, где (x_k,y_k,z_k)- произвольная точка участка , ∆_k - длина участка. Переходя к пределу, когда в соотв. с опр. КРИ-1 получаем, что масса мат. нити есть КРИ-1, т.е. m_L= Итак, предл.1: Масса мат. нити равна КРИ-1 от плотности распределения массы вдоль этой нити.

Экономический смысл:

Опр1. Пусть стоимость доставки груза по пути L длины l равна p, тогда частное p/l наз-ся средней удельной стоимостью доставки груза. Опр2. Удельной стоимостью доставки груза ML наз-ся предел средней удельной ст-ти вдоль участка L содержащего точку M, при стягивании этого участка в т. M

предл.2: Стоимость доставки груза равна КРИ-1 от удельной стоимости этой доставки по пути, т.е. P_L=

Геометрический смысл:

Рассмотрим поверхность H, в которой:

1)образующие этой поверхности параллельны оси 0Z 2) направляющей явл. кривая L 3) снизу поверхность H ограничена кривой L 4) сверху пов. H задана уравн. z=f(x,y)

предл.3: площадь цилиндрической поверхности может быть выражена с помощью КРИ-1 след. образом:

mesH =