Линейные скорость и ускорение точек вращающегося тела.

Покажем, что, зная величины угловой скорости W и условия ускорения E, можно легко найти и векторы скорости и ускорений в любой точке вращающегося тела, отстоящей на расстоянии h от оси.

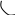
О

М

Поскольку траектория точки М во вращательном движении известно - это дуга окружности радиуса ОМ=h, для то определения скорости и ускорений удобно использовать естественная способ задания движения, принимая в качестве криволинейной координаты длину дуги окружности ММ .

Тогда: =

(1)

Таким образом, величина скорости ваг вращательном движении есть произведение расстояния h на угловую скорость тела.

Вектор точки М направлен по касательной к окружности радиуса ОМ, т.е. ортогонально этому радиусу. Отсюда следует эпюра скоростей точек вращающегося тела, лежащих на одном радиусе.

М

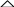
о

Касательное ускорение по величине будет:

(2)

Касательное ускорение равно произведению расстояния h на угловое ускорение тела.

Замечание: в формуле (2) E может быть как больше, так и меньше нуля.

В первом случае вектор направлен в сторону скорости, во втором – в противоположную. Для определения величины нормального ускорения так же применим общую формулу нормального ускорения из кинематики точки:

(3)

Таким образом, нормальное ускорение по величине не есть произведение расстояния h на квадрат угловой скорости.

Полное ускорение будет тогда:

(4) Из формул 1-4 видно, что, зная и E, можно полностью определить векторы

Замечание: поскольку и также пропорциональны h, то получаем аналогичное правило для определения эпюры ускорений.

M

E

O

Все векторы ускорений точек на радиусе OM параллельны , т.е. ускорению точек на ободе диска.

Частные случаи вращательного движения.

1) Равномерное вращение – вращение с постоянной угловой скоростью.

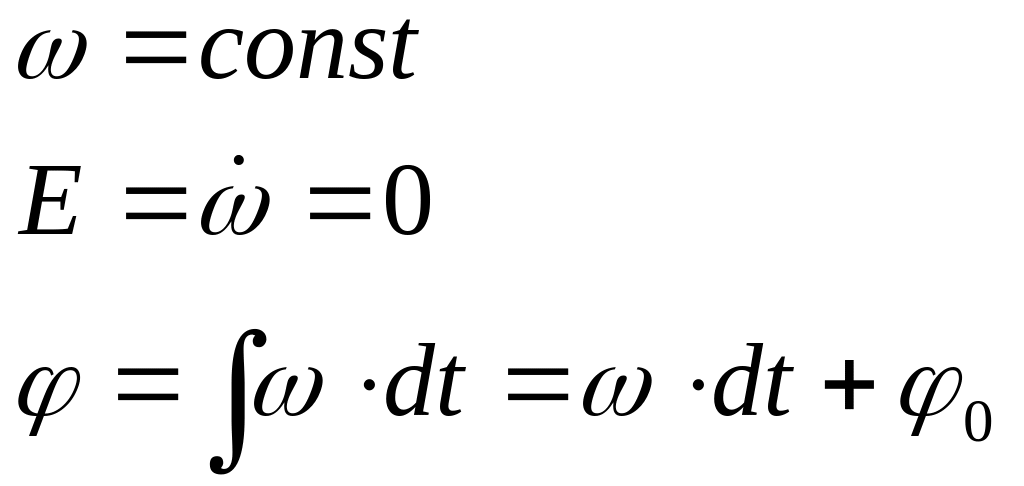
0

При равномерном вращении угол поворота линейно возрастает во времени.

2)Равнопеременное вращение – вращение с постоянным угловым ускорением. Так же как и в случае равнопеременного движения точки здесь выделяют равноускоренное вращение (E>0) и равнозамедленное (E<0)

здесь: - начальная угл. скорость

0

т.е. формулы для и здесь полностью аналогичны формулам для величины скорости и криволин. координаты S при равнопеременном движении точки.

В частном случае равноускоренного вращения при нулевой начальной скорости можно получить простую формулу для полного угла поворота, зная конечную угловую скорость.

здесь - конечная угловая

скорость, соотв. моменту

0

Пример:

R

o

Дано:

Найти:

(полное число оборотов)

Решение:

(случай равноускор. Вращения)

0

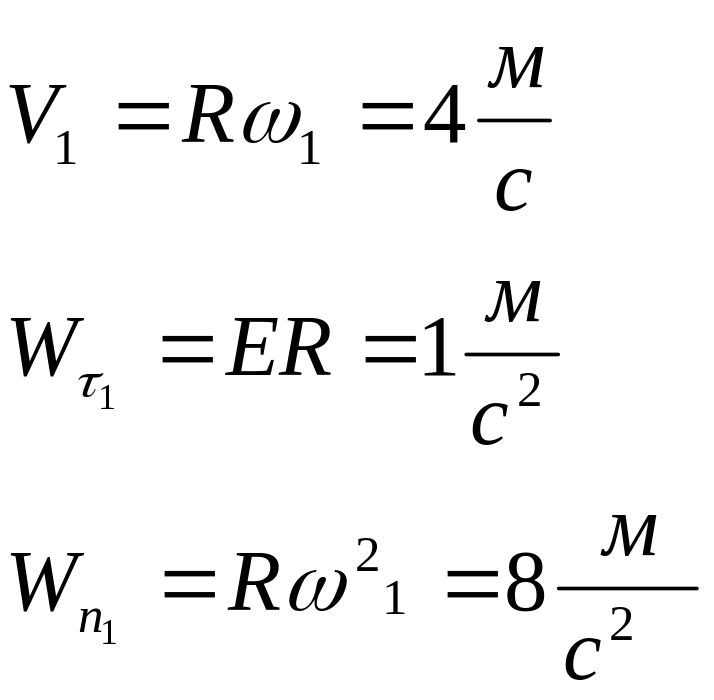
0

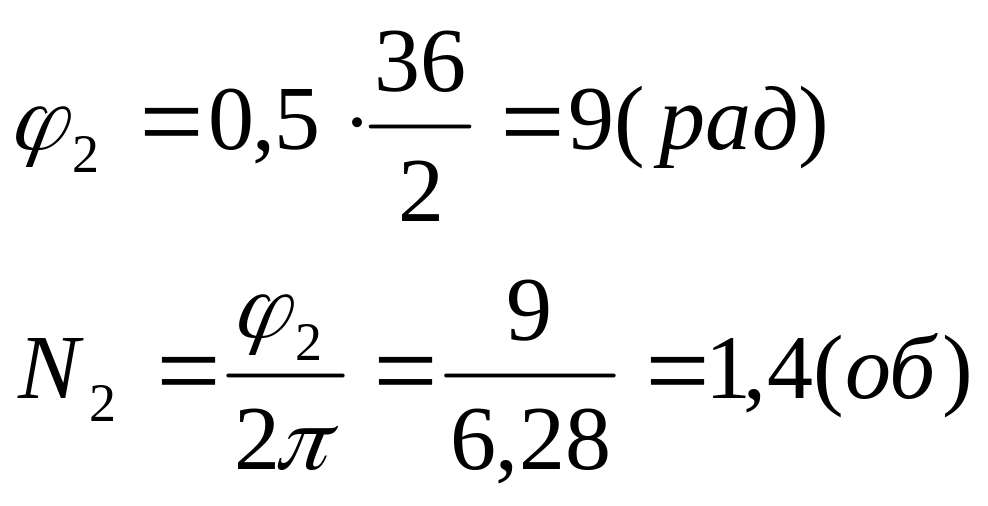
Векторные формулы скорости и ускорения точек вращающегося тела.

Будем определять вектор точки вращающегося тела, угловая скорость которого , отсчитывается от произвольной точки, но оси. Вектор точки, отсчитываемый от того же начала . Покажем, что для скорости точки справедливо векторное равенство:

(1)

z

B

o

M

A

По определению векторного приведения величина его здесь будет (*) . Здесь, как следует из

получим обычную скалярную скорость во вращательном движении. Тем самым доказали равенство (1) по величине. По направлению векторное произведение (1) должно быть направлено перпендикулярно плоскости в ту сторону, откуда поворот вектора к вектору на наименьший угол виден против часовой стрелки. Все то же самое можно сказать и о направлении вектора . Таким образом, равенство (1) обосновали и по направлению. Для полного ускорения точки продифференцируем (1) по времени используя правило дифференцирования векторных произведений:

E

В результате приходим к равенству: (2) это формула Ривальса.

Можно доказать, что первое векторное произведение здесь представляет касательное ускорение точки, а второе нормальное ускорение:

(3)