
- •Кинематика.
- •Векторный способ.
- •Координатный способ.
- •Естественный способ.
- •Связь между естественным и координатными способами.
- •Введем обозначения
- •Скорость и ускорение точки.
- •Ускорение точки.
- •Скорость и ускорение точки при координатном способе задания движения.
- •Скорость точки при естественном способе.
- •Ускорение точки при естественном способе. Касательное и нормальное ускорения.
- •Частные случаи движения точки.
- •Простейшие движения твердого тела
- •Линейные скорость и ускорение точек вращающегося тела.
- •Частные случаи вращательного движения.
- •Сложное движение точки.
- •Теорема сложения скоростей и ускорений в составном движении.
- •Плоско-параллельное движение твердого тела и его свойства
- •Скорости точек при плоском движении. Определение их методом полюса.
- •Мгновенный центр скоростей (мцс). Определение скоростей точек при плоском движении методом мцс.
Частные случаи движения точки.
Равномерное движение. Это движение, при котором скорость точки постоянна по величине, V=const.
Замечание:
траектория точки при этом может быть
криволинейной. При этом
![]() ,
,
![]() - начальная криволинейная координата.
- начальная криволинейная координата.
![]() ,
т.е. при равномерном движении полное
ускорение состоит только из нормального
,
т.е. при равномерном движении полное
ускорение состоит только из нормального
![]() .
.
Прямолинейное движение (не обязательно равномерное).
Для
прямолинейной траектории радиус кривизны
, тогда
![]() ,
т.е. в этом случае полное ускорение,
наоборот, состоит из касательного
,
т.е. в этом случае полное ускорение,
наоборот, состоит из касательного
![]()
Равномерное движение – движение с постоянным по величине и знаку касательным ускорением,
 .
Обычно этот случай разделяют на два:
равноускоренное движение, когда
.
Обычно этот случай разделяют на два:
равноускоренное движение, когда
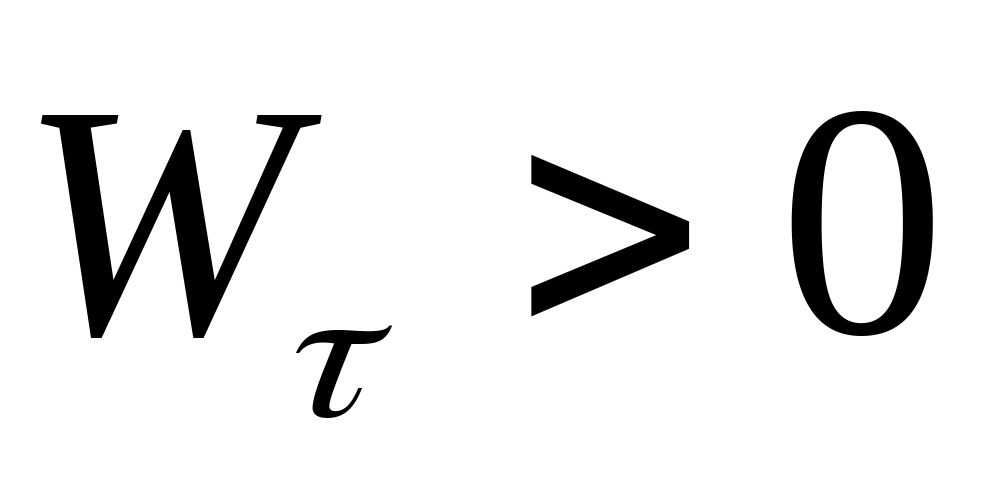 ,
и равнозамедленное
,
и равнозамедленное
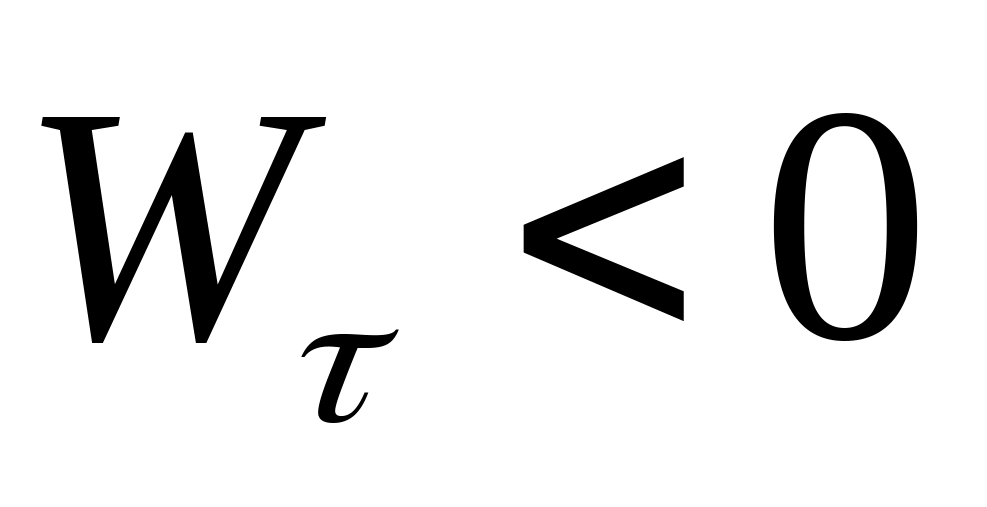 .
В обоих случаях справедливы равенства:
.
В обоих случаях справедливы равенства:
![]()
![]() V0
– начальная скорость
V0
– начальная скорость
![]() -
начальная координата, обычно полагается
=0, т.е. при равнопеременном движении
скорость изменяется по линейному закону,
а криволинейная координата
по квадратичному во времени.
-
начальная координата, обычно полагается
=0, т.е. при равнопеременном движении
скорость изменяется по линейному закону,
а криволинейная координата
по квадратичному во времени.
Простейшие движения твердого тела
К простейшим в кинематике относят два типа движений: поступательное движение и вращение вокруг неподвижной оси.
Поступательное движение – движение, при котором любая прямая, проведенная в нем, остается параллельна самой себе.
Примеры: движение кузова автомобиля на прямолинейной дороге (в этом случае траектории всех точек кузова – это параллельные прямые); круговое поступательное движение:
 С
С
 А В АВ
- спарник
А В АВ
- спарник


 О
О1
О
О1

Если длины кривошипов равны ОА=О1В, то спарник АВ совершает поступательное круговое движение, т.е. все его точки движутся по окружностям одинаковых радиусов, но со сдвинутыми центрами.
Вообще траекториями точек тела при поступательном движении могут быть любые кривые.
Справедлива теорема: при поступательном движении тела траектории всех его точек равны, т.е. при наложении совпадают, а скорости и ускорения векторно равны.






 Z
B/
Z
B/
 A/
A/
![]()
![]() 1 2
1 2
y
x
Выделим
в теле, движущемся поступательно, отрезок
АВ. Поскольку при движении он сохраняет
параллельность, а величина его также
неизменна (как расстояние между точками
твердого тела), то
![]() .
Последнее означает, что траектория
точки В получается из траектории точки
А ее параллельным переносом на вектор
.
Последнее означает, что траектория
точки В получается из траектории точки
А ее параллельным переносом на вектор
![]() ,
т.е. траектории
действительно равны, т.к. при наложении
совпадут.
,
т.е. траектории
действительно равны, т.к. при наложении
совпадут.
Рассмотрим
векторный треугольник ОАВ. Из него
видно, что
![]() .
Будем дифференцировать это равенство
по времени
.
Будем дифференцировать это равенство
по времени
![]() ,
т.е.
,
т.е.
![]() .
Доказали равенство скоростей. Дифференцируя
его также по времени, подучим и равенство
ускорений точек
.
Доказали равенство скоростей. Дифференцируя
его также по времени, подучим и равенство
ускорений точек
![]() .
.
Следствие: из доказанной теоремы видно, что все точки тела при поступательном движении движутся одинаково, поэтому при поступательном движении можно говорить о скорости, ускорении и траектории такого движения, приписывая их к любой точки тела.
Вращательное движение.
Р



 ассмотрим
простейшее вращательное движение, когда
тело вращается вокруг неподвижной оси
Z.
ассмотрим
простейшее вращательное движение, когда
тело вращается вокруг неподвижной оси
Z.
 Z
Z
М0 О
М
При таком вращении точки тела, лежащие на оси, остаются неподвижными, а любая точка М, отстающая от оси на расстоянии ОМ=h, будет совершать движение по окружности радиуса h с центром на оси. Плоскости таких окружностей перпендикулярны оси.
Для
того, чтобы задать вращательное движение
достаточно для любой точки М тела, не
лежащей на оси задать угол
![]() ,
где М0
– положение этой точки в начальный
момент времени t0=0.
Угол φ в радианах называется угловой
координатой тела, а уравнение
,
где М0
– положение этой точки в начальный
момент времени t0=0.
Угол φ в радианах называется угловой
координатой тела, а уравнение
![]() (1) называется уравнением или законом
вращения. Положительное направление
отсчета φ принимают против часовой
стрелки, если смотреть с положительного
направления оси Z.
Основными кинематическими характеристиками
вращательного движения являются его
угловая скорость и угловое ускорение
тела.
(1) называется уравнением или законом
вращения. Положительное направление
отсчета φ принимают против часовой
стрелки, если смотреть с положительного
направления оси Z.
Основными кинематическими характеристиками
вращательного движения являются его
угловая скорость и угловое ускорение
тела.
Угловая
скорость определяет изменение угла φ
во времени. Пусть в момент t
угловая координата была φ, а в последующий
момент t1>t
она стала φ1,
т.е. за время Δt=
t1-t
угловая координата получает приращение
Δφ=φ1-φ,
тогда средней угловой скоростью за
время Δt
называется величина
![]() (2).
(2).
![]() тем точнее характеризует изменение
угла φ, чем меньше Δt
, поэтому, перейдя здесь к пределу при
,
получим точное значение угловой скорости
в момент t
тем точнее характеризует изменение
угла φ, чем меньше Δt
, поэтому, перейдя здесь к пределу при
,
получим точное значение угловой скорости
в момент t
![]() или
или
![]() (3)
(3)
Таким образом,
мгновенная угловая скорость – есть
производная угловой координаты по
времени. Заметим, что
![]() может быть разных знаков в зависимости
от того, в какую сторону вращается тело:
при положительном направлении вращения
>0,
т.к.
может быть разных знаков в зависимости
от того, в какую сторону вращается тело:
при положительном направлении вращения
>0,
т.к.
![]() возрастает.
возрастает.
[W]=рад/с=с-1
В технике часто для измерения угловых скоростей многооборотных вращений (турбин, валов и т.д.) применяют внесистемную единицу измерения угловых скоростей [n]=об/мин
![]()
Угловое ускорение характеризует изменение угловой скорости во времени, так, если за тот же промежуток времени Δt угловая скорость изменялась от W до W1, т.е. получила приращение ΔW=W1-W, то угловое ускорение будет
![]() (4)
(4)
Переходя в
(4) к пределу, получим мгновенное угловое
ускорение, т.е. ускорение в момент t:
![]()
![]() (5), т.е. угловое ускорение в данный момент
есть производная от угловой скорости.
Учитывая определение W ,
получим
(5), т.е. угловое ускорение в данный момент
есть производная от угловой скорости.
Учитывая определение W ,
получим
![]() (6), т.е. это также вторая производная от
угловой координаты [ε]=рад/с2=с-2
. Вращение будет ускоренным (т.е. величина
W возрастает), если W
и ε одинаковых знаков, и замедленным,
если они разных знаков.
(6), т.е. это также вторая производная от
угловой координаты [ε]=рад/с2=с-2
. Вращение будет ускоренным (т.е. величина
W возрастает), если W
и ε одинаковых знаков, и замедленным,
если они разных знаков.
В кинематике
часто используют векторные представления
угловой скорости и углового ускорения,
т.е. считают, что
![]() (7), где
(7), где
![]() - орт оси Z. Причем вектор
отсчитывают от любой точки на оси.
Угловое ускорение считают также вектором
- орт оси Z. Причем вектор
отсчитывают от любой точки на оси.
Угловое ускорение считают также вектором
![]() (8). Из (7) и (8) видно, что векторы W
и ε связаны равенством (5), т.е.
(8). Из (7) и (8) видно, что векторы W
и ε связаны равенством (5), т.е.
![]() (9). Вектор
(9). Вектор
![]() направлен в сторону
направлен в сторону
![]() ,
если вращение ускоренное, и в
противоположную сторону, если замедленное.
Величины W и ε разных
знаков.
,
если вращение ускоренное, и в
противоположную сторону, если замедленное.
Величины W и ε разных
знаков.

 В
В



 z
z
А
