Скорость и ускорение точки при координатном способе задания движения.

Пусть задан координатный способ, т.е. прямоугольные координаты точки известны как функции времени. Запишем связь между векторным и координатным способами.

(1)

Поскольку в (1) орты , , - постоянные векторные множители, то для определения скорости точки будем дифференцировать (1) по времени, применяя обычные правили дифференцирования, т.е. вынося в каждом из слагаемых орты за знак производной.

(2)

Если записать вектор также через его проекции на оси , то сравнивая это равенство с (2), находим , , (3), т.е. проекциями скорости при координатном способе будут производные от соответствующих прямоугольных координат точки.

Величина скорости будет (4), направление можно определить направляющими косинусами, т.е. косинусами углов между вектором скорости и осями координат:

(5)

Как для направляющих косинусов справедливо тождество (6). Ход определения ускорения при координатном способе полностью аналогичен приведенным вычислениям для скорости. В частности при вычислении вектора ускорения следует дифференцировать равенство (2) для скорости, тогда, применяя те же правила дифференцирования, получим

(7)

т.е. сразу получаем проекции ускорения , , (8), они равны вторым производным от соответствующих координат.

Величина ускорения так же будет

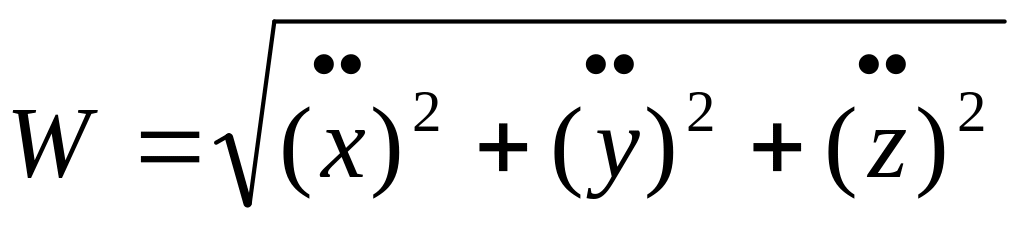(9),

а направление, по аналогии со скоростью, определяют по направляющим косинусам:

(10)

Для этих косинусов также справедливо тождество (6).

Формулы (2)-(10) полностью определяют векторы скорости и ускорения при координатном способе.

Скорость точки при естественном способе.

_ O

М,t,S

M₁,t₁,S₁

О^/

+

Пусть при естественном способе т. М в момент t имела криволинейную координату S, а в последующий момент t₁ в положении М₁ эта координата стала S₁, значит за время Δt=t₁-t>0 криволинейная координата изменяется на ΔS=S₁-S. Для простоты считаем, что ΔS>0, т.е. точка движется в положительном направлении. Введем также векторный способ задания движения, т.е. т. О^/ начала отсчета радиус-вектора движущейся материальной точки. Запишем вектор скорости точки М через предел

Величина скорости тогда будет: (*).

При вычислении придела (*) величина вектора перемещения, т.е. близка к соответствующей длине дуги, т.е. ΔS. Это эквивалентная бесконечно малая (если траектория – гладкая кривая), т.е. , при , .

Поэтому в пределе (*) величину заменим на эквивалентную, т.е. ΔS, тогда или (1), т.е. скорость по величине есть производная от криволинейной координаты по времени.

Замечание: равенство (1) записано в предположении, что координата S возрастает, т.е. что . В общем случае аналогично доказывается, что величина скорости будет (2).

Для записи вектора скорости при естественном способе вводят орт касательной к траектории, направленный в сторону скорости, тогда записывается просто: (3), где величина V определяется формулами (1) или (2).