Выборочная медиана

МЕДИАНА ВЫБОРОЧНАЯ — (от лат. mediana средняя) срединное значение упорядоченной: выборки случайных величин M. в. равна срединному случайному числу M= х(n+1)/2, если n нечётно, и ср. значению двух последоват. срединных чисел если и четно. M. в. является устойчивой… 

№10 выборочная дисперсия, выборочное ско

Выборочная дисперсия – точечная оценка для параметра  , который называют генеральной дисперсией.

Def: выборочной дисперсией называют статистику   (3).

Для дискретной случайной величины:

, где 

Докажем, что выборочная дисперсия  является состоятельной, но смещенной оценкой параметра  :

Получим вспомогательное утверждение (лемму):

Для любого  справедливо равенство    (4)

В (4) возьмем  с = 0. Получим:

. Обозначим  . Тогда:

  (3’).

Доказательство.

Рассмотрим последовательность случайных величин:

Применим к ней теорему Чебышева:

. В левой части –  . Вычислим правую часть. Для этого воспользуемся (4):

что выборочная дисперсия дает смещенную оценку. Вместе с тем, при  . Поэтому в силу теоремы Чебышева:

. Таким образом, выборочная дисперсия является состоятельной оценкой.

Исправленная выборочная дисперсия

Добавил admin | Рубрики: Алгебра

Получим несмещенную оценку для генеральной дисперсии  :

Def: Статистику  называют исправленной выборочной дисперсией.

Очевидно, что  - несмещенная и состоятельная оценкадля параметра  :

Проверим несмещенность:

Замечание: так как при  , то на практике для оценки  применяют (3’) ввиду ее удобства.

В качестве оценок для среднего квадратичного отклонения  берут статистики  и  .Можно показать, что это – состоятельные оценки: 

но обе оценки будут смещенными:

Интервальные оценки неизвестных параметров распределения.

1) Интервальная оценка и ее надежность.

Рассмотрим выборку  . Совокупность независимых случайных величин имеет тот же закон распределения, что и  .

Пусть  статистики такие, что всегда  , тогда   – случайный интервал.

 – оцениваемый параметр.

Def: если случайный интервал  может покрывать неизвестный параметр  , то этот интервал называется интервальной оценкой для параметра  .

Пусть вероятность того, что параметр  , тогда  вероятность   называется надежностью или доверительной вероятностью интервальной оценки  .

Естественно, что значения   берут близкими к единице. Обычно  берут 0.95, 0.99, 0.999.

С повышением надежности оценки увеличивается длина доверительного интервала.

2) Доверительный интервал для нормально распределенной случайной величины при известной дисперсии  .

Рассмотрим случайную величину     – известная величина. Требуется построить доверительный интервал  .

Для решения данной задачи рассмотрим статистику   – выборочная средняя. Можно показать, что   также подчинена нормальному закону.

Для нормального распределения случайной величины справедливо равенство:

 – функция Лапласа.

Применим равенство (2) к выборочной средней:

Выберем   так, что бы   – заданная надежность оценки.

Из (3) имеем:  .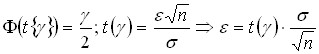

Итак, доверительный интервал для параметра   имеет вид:

Здесь   выбирается из таблицы значений функций Лапласа: 

3) Доверительный интервал для генеральной средней при неизвестной дисперсии  .

Как и прежде 

Рассмотрим статистику  . Здесь   – исправленная выборочная дисперсия. Доказано, что статистика  имеет закон распределения с плотностью:

 – числа.

Распределение вероятностей, задаваемое плотностью (5) называют “t” – распределением или распределением Стьюдента с   степенью свободы.

Функция (5) является четной.

При   “t” – распределение стремится к нормальному распределению.

Что бы записать доверительный интервал для генеральной средней, рассмотрим равенство:

Пользуясь таблицами t” – распределения по заданной надежности и числу степеней свободы  , выбираем  из условия (6):

В результате с надежностью   в силу (6) выполняется двойное неравенство:

Отсюда выражаем “a”:

Выборочное среднее квадратическое отклонение дает более точную оценку параметра о, чем выборочный размах или крайние значения, но при этом усложняются расчеты. Точность метода средних квадратических отклонений с увеличением объема выборки повышается, а точность метода размахов понижается. При 10 метод размахов применять не рекомендуется, его целесообразно заменять методом средних размахов. [1]

Вычислим выборочную среднюю и выборочное среднее квадратическое отклонение методом произведений. [2]

Известно несколько способов проверки ох, в частности, по выборочному среднему квадратическому отклонению s, по межквар-тильной разности, способом группировки, с помощью размахов. Рассмотрим первый и последний из перечисленных способов, применяемые чаще других. [3]

Произведено 12 измерений напряжения радиосигнала одним и тем же прибором, не имеющим систематической ошибки, причем выборочное среднее квадратическое отклонение s случайных ошибок оказалось равным 0 6 В. [4]

Произведено 12 измерений напряжения радиосигнала одним и тем же прибором, не имеющим систематической погрешности, причем выборочное среднее квадратическое отклонение S случайных погрешностей оказалось равным 0.6 В. [5]

Известно, что в качестве оценок математического ожидания и среднего квадратического отклонения случайной величины X можно принять соответственно выборочную среднюю х и выборочное среднее квадратическое отклонение ав. [6]

Коэффициент смещения Е, применяемый для нормального закона распределения и законов типа А и модуля разности, пред - Обозначения: б - допуск; X - выборочное среднее; S - выборочное среднее квадратическое отклонение; 5ср - среднее значение признака качества ( например, координата середины поля допуска); т - выборочный эксцесс. [7]

Когда обнаружены действительно анормальные результаты наблюдений и они иключены из обрабатываемой выборки, то на основе оставшихся результатов наблюдений по ГОСТ 8.207 - 76 будут определены: среднее арифметическое X исправленных результатов наблюдений, выборочное среднее квадратическое отклонение Sx результата наблюдения и 5 - результата измерения, выборочная доверительная погрешность измерения Д -, другие характеристики. [8]

Путем обмера партии валов найдены частоты фактических размеров и с помощью вероятностной бумаги установлено, что опытное распределение приближенно нормально. С помощью той же бумаги найдено выборочное среднее 31 974 мм и выборочное среднее квадратическое отклонение 5 0 004 мм. [9]

Температура внутри установки измеряется в и 5 точках. По результатам контроля к40 выборок по и 5 наблюдений в каждой рассчитаны средняя арифметическая х 202 С и выборочное среднее квадратическое отклонение s 2 5 С. [10]

При контроле по количественному признаку в ряде случаев среднее квадратическое отклонение а контролируемого параметра заранее бывает известно ( например, когда технологический процесс стабилен) либо неизвестно. Если среднее квадратическое отклонение а известно, то используется а-план выборочного контроля. Этот метод предусматривает наименьший объем выборки по сравнению с другими методами и требует меньше вычислений. Если среднее квадратическое отклонение 0 неизвестно, стандарт предусматривает два метода его оценки: по выборочному среднему квадратическому отклонению 5 и по размаху. В первом случае используется S-план выборочного контроля, во втором случае - R-илгн выборочного контроля. С теоретической точки зрения предпочтительнее оценивать среднее квадратическое отклонение а по выборочному среднему квадратическому отклонению 5, а не по размаху R, так как первый метод оценки дает более точные результаты. Поэтому S-метод является основным методом оценки при контроле качества продукции по количественному признаку, даже несмотря на то, что он требует более сложных вычислений, чем - метод. При использовании - метода следует иметь в виду, что чем больше объем выборки, тем меньше информации дает ее размах о значении среднего квадратического отклонения о. При объеме выборки больше восьми единиц продукции оценивать среднее квадратическое отклонение по размаху вообще не рекомендуется. [11]

При контроле по количественному признаку в ряде случаев среднее квадратическое отклонение а контролируемого параметра заранее бывает известно ( например, когда технологический процесс стабилен) либо неизвестно. Если среднее квадратическое отклонение а известно, то используется а-план выборочного контроля. Этот метод предусматривает наименьший объем выборки по сравнению с другими методами и требует меньше вычислений. Если среднее квадратическое отклонение 0 неизвестно, стандарт предусматривает два метода его оценки: по выборочному среднему квадратическому отклонению 5 и по размаху. В первом случае используется S-план выборочного контроля, во втором случае - R-илгн выборочного контроля. С теоретической точки зрения предпочтительнее оценивать среднее квадратическое отклонение а по выборочному среднему квадратическому отклонению 5, а не по размаху R, так как первый метод оценки дает более точные результаты. Поэтому S-метод является основным методом оценки при контроле качества продукции по количественному признаку, даже несмотря на то, что он требует более сложных вычислений, чем - метод. При использовании - метода следует иметь в виду, что чем больше объем выборки, тем меньше информации дает ее размах о значении среднего квадратического отклонения о. При объеме выборки больше восьми единиц продукции оценивать среднее квадратическое отклонение по размаху вообще не рекомендуется. [12]

№11 точ. Оценки ген совокупности, мода, алгоритм вычисления, начальный и центральный моменты, асимметрия, эксцесс

Мода — значение во множестве наблюдений, которое встречается наиболее часто.Случайная величина может не иметь моды. Иногда в совокупности встречается более чем одна мода(например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.

Мода как средняя величина употребляется чаще для данных, имеющих нечисловую природу. Среди перечисленных цветов автомобилей — белый, черный, синий металлик, белый, синий металлик, белый — мода будет равна белому цвету. При экспертной оценке с её помощью определяют наиболее популярные типы продукта, что учитывается при прогнозе продаж или планировании их производства.

Кроме математического ожидания и дисперсии, для оценки случайной величины используются начальные и центральные моменты случайной величины.

Начальным моментом порядка   случайной величины  называют математическое ожидание величины  :

.

Центральным моментом порядка   случайной величины   называют математическое ожидание величины  :

.

Начальный момент первого порядка   равен математическому ожиданию самой случайной величины  .

Центральный момент первого порядка равен нулю:

.

Центральный момент второго порядка представляет собой дисперсию случайной величины  :

.

Для дискретных случайных величин:

;

.

Коэффицие́нт асимметри́и (skewness) — числовая характеризующая степени несимметричности распределения данной случайной величины.

Определение

Пусть задана случайная величина  , такая что  .

Коэффициент асимметрии распределения случайной величины   определяется формулой:

где

 — третий центральный момент случайной величины  ;

 — стандартное отклонение случайной величины  ;

 — дисперсия или второй центральный момент случайной величины  ;

Если плотность распределения симметрична, то  .

Если левый хвост распределения тяжелее, то  .

Если правый хвост распределения тяжелее, то  .

Иногда вместо   используется обозначение  .

Коэффицие́нт эксце́сса (kurtosis) — числовая характеризующая степени остроты пика распределения случайной величины.

Определение

Пусть задана случайная величина  , такая что  .

Коэффициент эксцесса распределения случайной величины   определяется формулой:

где

 — четвёртый центральный момент случайной величины  ;

 — дисперсия или второй центральный момент случайной величины  ;

Нормальное распределение имеет нулевой эксцесс,  .

Если хвосты распределения «легче», а пик острее, чем у нормального распределения, то  .

Если хвосты распределения «тяжелее», а пик более «приплюснутый», чем у нормального распределения, то  .

Область возможных значений эксцесса  .

№12 Интервальные оценки генеральной совокупности