Алгоритм вычисления пределов функций

1) Подставить точку в функцию, стоящую под знаком предела, и выяснить тип неопределенности.

2) Если в результате подстановки получилось число или , то задача решена.

3) Если получилась неопределенность вида при , а выражение, стоящее под знаком предела, представляет собой частное двух полиномов или иррациональных функций, то в числителе и знаменателе этого выражения нужно вынести в старшей степени. Если старшие степени числителя и знаменателя равны, то значение предела равно отношению коэффициентов при старших степенях в числителе и знаменателе (см. пример 1). Если степень числителя больше степени знаменателя, то значение предела равно бесконечности. Если степень числителя меньше степени знаменателя, то значение предела равно нулю.

4) Если получилась неопределенность вида при , а выражение, стоящее под знаком предела, представляет собой частное трансцендентных функций, то это выражение следует преобразовать таким образом, чтобы получилось одно из выражений, представленных в таблице некоторых значений переделов функций.

5) Если получилась неопределенность вида при , а выражение, стоящее под знаком предела, представляет собой частное двух полиномов, то числитель и знаменатель выражения следует разложить на множители, общие множители сократить, а затем вычислить предел, используя свойства пределов (см. пример 2).

6) Если получилась неопределенность вида при , а выражение, стоящее под знаком предела, представляет собой отношение трансцендентных функций, то это выражение следует преобразовать таким образом, чтобы получилось произведение или частное замечательных пределов или следствий из них, а затем вычислить предел, используя свойства пределов (см. пример 3).

7) Если получилась неопределенность вида при , то выражение, стоящее под знаком предела, следует преобразовать таким образом, чтобы получился второй замечательный предел, а затем вычислить предел от степени числа , используя свойства пределов (см. пример 4).

Пример 1. Вычислить предел функции .

Решение. .

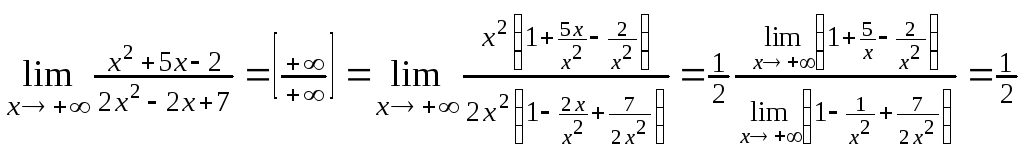Пример 2. Вычислить предел функции .

Решение. .

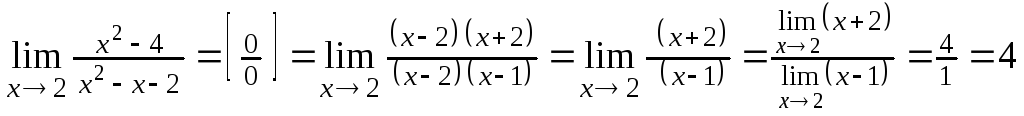Пример 3. Вычислить предел функции .

Решение.

.

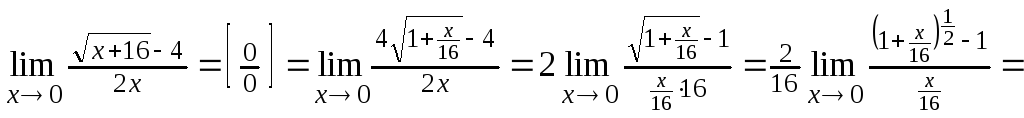
Пример 4. Вычислить предел функции .

Решение.

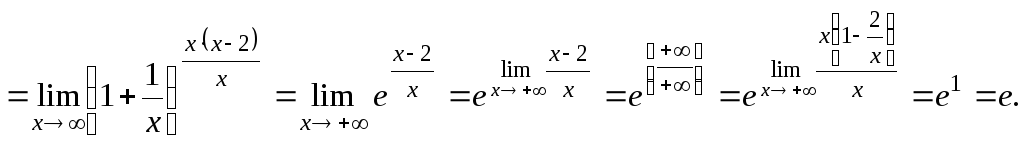
Теоретический материал: [1, гл. 6], [2, гл. 4], [3, гл. 3], [5], [8], [10], [12, гл. 3], [17], [19], [21], [27], [33, ч. 1, гл. 6], [40, т. 1, гл. 3].

Задания для решения на практическом занятии

1. Вычислить предел функции:

а), б), в), г), д), е) , ж) , з) , и) , к), л), м), н), о), п) , р) , с) , т) , у) , ф) , х) , ц) .

Задания для самостоятельной работы

1. Вычислить предел функции:

а), б), в), г), д), е) , ж) , з) , и) , к), л), м), н), о).

Тема 10. Свойства функций. Непрерывность функции

10.1. Свойства функций

Определение 1. Функцию называют четной, если вместе со всяким и выполняется равенство .

Определение 2. Функцию называют нечетной, если вместе со всяким и выполняется неравенство .

Определение 3. Функцию называют периодической, если существует число , что вместе со всяким и .

Определение 4. Функцию называют монотонно возрастающей (строго монотонно возрастающей) на числовом множестве , если для любых из неравенства следует неравенство ().

Определение 5. Функцию называют монотонно убывающей (строго монотонно убывающей) на числовом множестве , если для любых из неравенства следует неравенство ().

Возрастающие и убывающие функции объединяют общим названием монотонные функции.

Определение 6. Пусть функция задана на множестве с областью значений . Если каждому соответствует единственное значение , при котором . Тогда полученную функцию , определенную на множестве с областью значений , называют обратной функцией к функции .

10.2. Преобразования графика функции

Пусть задан график функции . Тогда справедливы следующие утверждения:

1. График функции есть график функции , сдвинутый (при влево, при вправо) на единиц параллельно вдоль оси .

2. График функции есть график функции , сдвинутый (при вверх, при вниз) на единиц параллельно вдоль оси .

3. График функции есть график функции , растянутый (при ) в раз или сжатый (при ) вдоль оси . При график функции есть зеркальное отражение графика функции относительно оси .

4. График функции () есть график функции , сжатый (при ) или растянутый (при ) вдоль оси . При график функции есть зеркальное отражение графика функции относительно оси .

10.3. Непрерывность функции

Определение 7. Функцию называют непрерывной в точке , если точка является предельной для и существует .

Определение 8. Приращением аргумента в точке называют величину

.

Определение 9. Приращением функции в точке называют величину

.

Определение 10. Функцию называют непрерывной в точке _, если точка является предельной для и.

Определение 11. Если функция непрерывна в каждой точке промежутка , то ее называют непрерывной на промежутке .

Пример 1. Доказать, что функция непрерывна в точке .

Решение. 1) Вычислим : .

2) Вычислим : .

3) Составим приращение : .

4) Вычислим .

Следовательно, функция непрерывна в точке по определению 10.

Свойства функций, непрерывных в точке

1. Если функции , непрерывны в точке , то сумма (разность), произведение и частное (при условии, что в окрестности точки ) этих функций также непрерывны в точке .

2. Пусть у функции существует предел при , , а функция непрерывна в точке . Тогда у сложной функции существует предел при , причем .

3. Пусть функция непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция непрерывна в точке , причем .

Свойства функций, непрерывных на промежутке

1. Если функция непрерывна на отрезке , то она ограничена на этом отрезке и достигает на нем своих наибольшего и наименьшего значений.

2. Если функция определена и непрерывна на отрезке , то множество ее значений является отрезком.

3. Если функция непрерывна на отрезке и принимает на концах этого отрезка значения разных знаков, то существует хотя бы одна точка такая, что .

4. Если функция определена, непрерывна и строго монотонна на отрезке , то у нее существует обратная функция , определенная, непрерывная и строго монотонная того же знака на отрезке .