
- •Линейные уравнения и системы линейных дифференциальных уравнений с постоянными коэффициентами
- •§1. Линейные уравнения с постоянными коэффициентами
- •§ 2. Линейные нормальные системы с постоянными коэффициентами
- •Дифференциальные уравнения первого порядка
- •4. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли.
Дифференциальные уравнения первого порядка
1. Общее дифференциальное уравнение первого порядка. Уравнения, связывающие независимую переменную, искомую функцию и ее производные, называются дифференциальными.
Если искомая функция зависит от одной переменной, то дифференциальное уравнение называют обыкновенным.
Дифференциальным
уравнением первого порядка
называют уравнение вида
![]() или, разрешенное
относительно
или, разрешенное
относительно
![]()
![]() .
(1)
.
(1)
Задача
Коши:
найти решение
![]() уравнения (1), удовлетворяющее начальному
условию
уравнения (1), удовлетворяющее начальному
условию
![]() .
(2)
.
(2)
Решением уравнения
(1) называется такая дифференцируемая
функция
![]() ,
которая при подстановке в уравнение
обращает его в тождество. Функция
на плоскости изображает кривую, называемую
интегральной
кривой.
,
которая при подстановке в уравнение
обращает его в тождество. Функция
на плоскости изображает кривую, называемую
интегральной
кривой.
Общим решением
дифференциального уравнения
(1) в области
![]() называется функция
называется функция
![]() ,
зависящая от одной произвольной
постоянной C,
и такая, что выполняются условия:
,
зависящая от одной произвольной
постоянной C,
и такая, что выполняются условия:
1) она удовлетворяет
уравнению (1) при любых значениях
постоянной
![]() ;
;
2)каково бы ни было
начальное условие (2), можно подобрать
значение
![]() постоянной C
такое, что решение
постоянной C
такое, что решение
![]() будет удовлетворять заданному начальному
условию (2). При этом предполагается, что
в любой точке
будет удовлетворять заданному начальному
условию (2). При этом предполагается, что
в любой точке
![]() выполняются условия существования и
единственности решения задачи Коши
(1), (2).
выполняются условия существования и
единственности решения задачи Коши
(1), (2).
Теорема существования и единственности решения задачи Коши (теорема Пикара). Если правая часть уравнения (1) функция
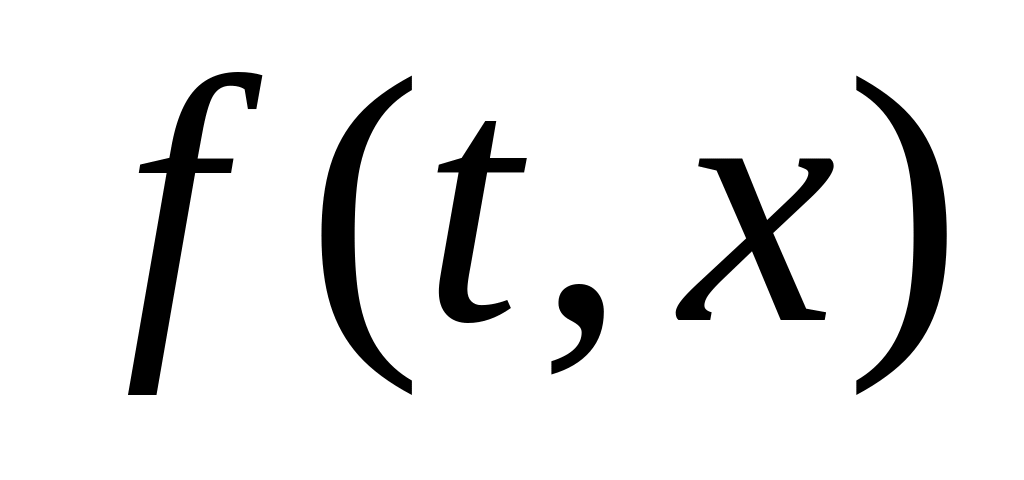 ,
непрерывная в замкнутой области
,
непрерывная в замкнутой области
 (
(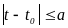 ,
,
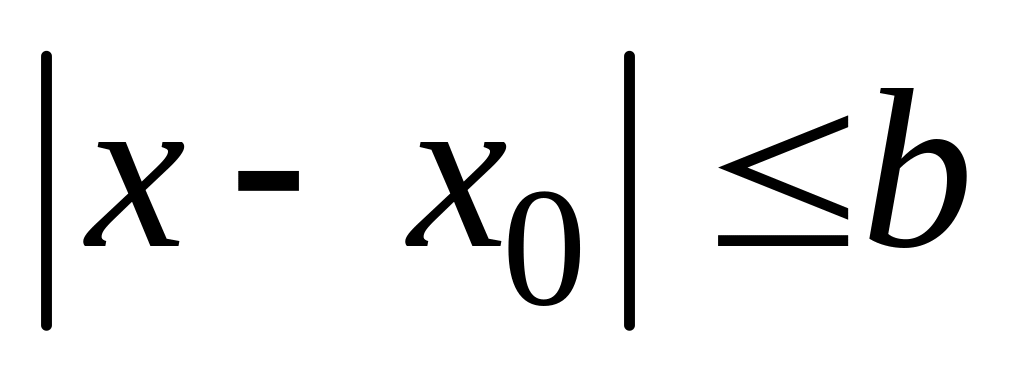 ),
а, значит, ограниченная
),
а, значит, ограниченная
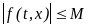 и удовлетворяет в
условию Липшица
и удовлетворяет в
условию Липшица
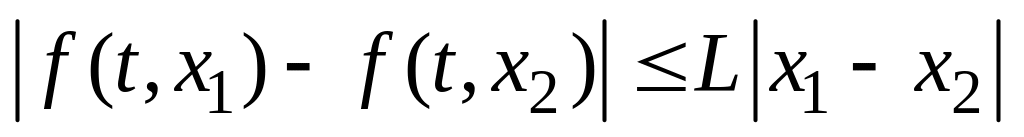 ,
где
,
где
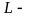 константа Липшица (
константа Липшица (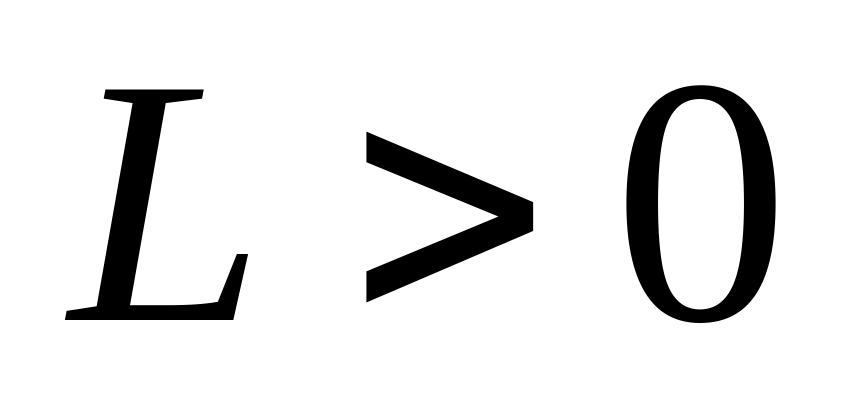 );
а
);
а
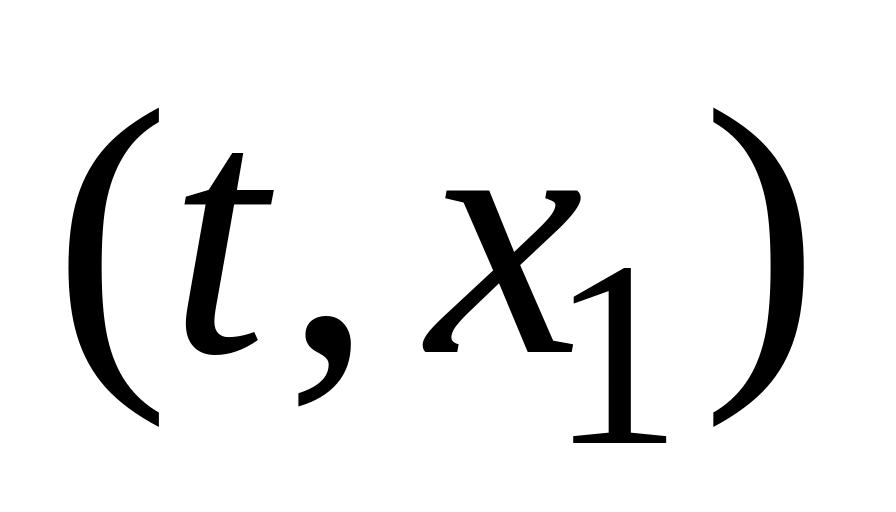 и
и
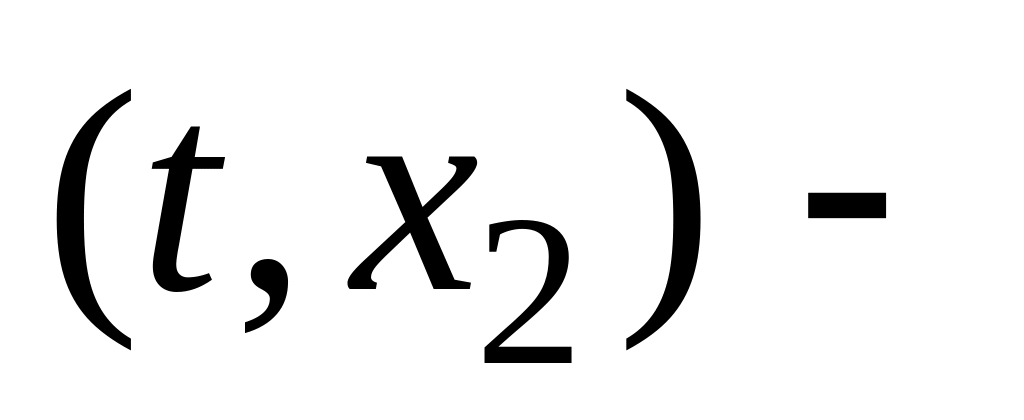 любые две точки из области
,
то существует единственное решение
уравнения (1), удовлетворяющее начальному
условию (2), и это решение определено,
непрерывно дифференцируемо в интервале
любые две точки из области
,
то существует единственное решение
уравнения (1), удовлетворяющее начальному
условию (2), и это решение определено,
непрерывно дифференцируемо в интервале
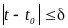 ,
где
,
где и не выходит при этих
из
области
и не выходит при этих
из
области
Доказательство. Заменим задачу Коши (1) с условием (2) эквивалентным интегральным уравнением
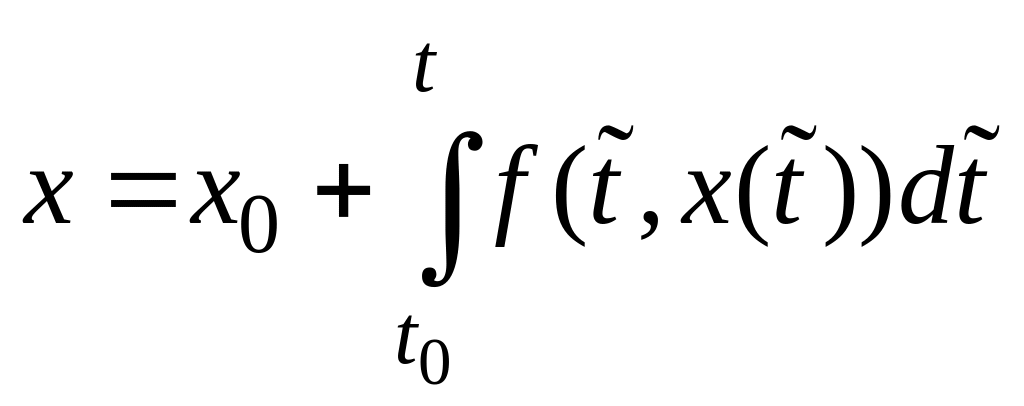 .
(3)
.
(3)
1) Докажем
существование непрерывных решений
уравнения (3) применяя метод последовательных
приближений Пикара.
За нулевое приближение
![]() примем функцию
примем функцию
![]()
Заменим
в (3) переменную
![]() нулевым приближением. Полученную функцию
возьмем в качестве первого приближения,
то есть
нулевым приближением. Полученную функцию
возьмем в качестве первого приближения,
то есть
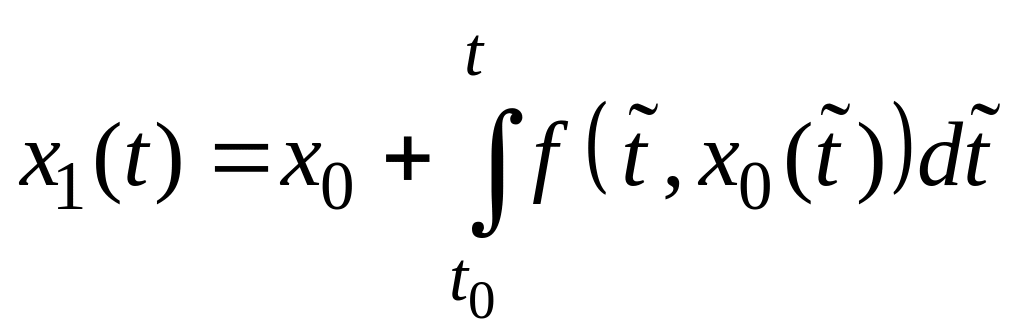 .
(4)
.
(4)
Аналогично получим
![]() и вообще, в качестве
-го
приближения возьмем функцию, определенную
соотношением
и вообще, в качестве
-го
приближения возьмем функцию, определенную
соотношением
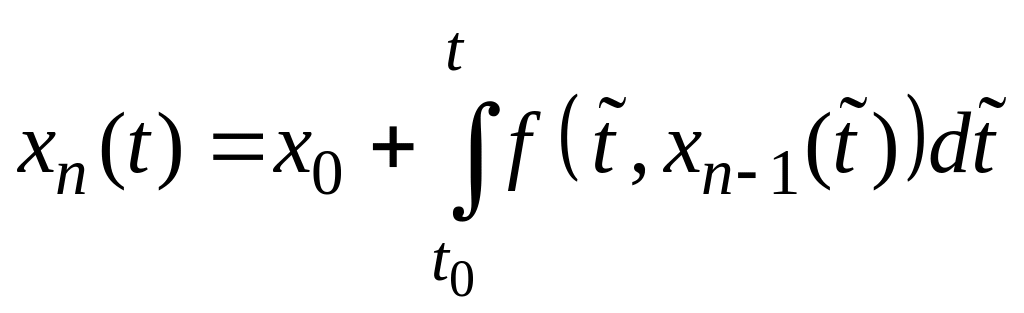 ,
,
![]() (5)
(5)
Таким
образом, построена последовательность
функций
![]() .
.
Покажем,
используя метод математической индукции,
что все функции последовательности
определены и непрерывны на некотором
промежутке
![]() и не выходят из замкнутой области
и не выходят из замкнутой области
![]() ,
то есть, что
,
то есть, что
![]() при
,
при
,
![]() (6)
(6)
Из (4) следует, что
функция
![]() определена и непрерывна на всем интервале
определена и непрерывна на всем интервале
![]() ,
так как функция
,
так как функция
![]() непрерывна на этом интервале, а
определенный интеграл, как известно, с
переменной верхней границей от непрерывной
функции представляет собой непрерывную
функцию своей верхней границы на этом
же интервале.
непрерывна на этом интервале, а
определенный интеграл, как известно, с
переменной верхней границей от непрерывной
функции представляет собой непрерывную
функцию своей верхней границы на этом
же интервале.
Используя формулу
![]() ,
имеем
,
имеем
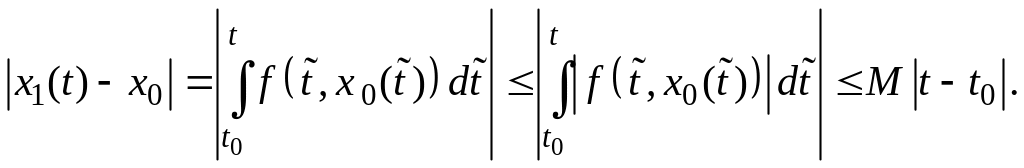 (7)
(7)
Таким
образом, если потребовать, чтобы
![]() то есть
то есть
![]() ,
то функция
,
то функция
![]() не покинет области
не покинет области
![]() .
Поэтому при
.
Поэтому при
![]() функция
определенна, непрерывна и содержится
в области
.
функция
определенна, непрерывна и содержится
в области
.
Допустим, что такое
утверждение имеет место для функции
![]() ,
и покажем, что оно выполняется и для
функции
,
и покажем, что оно выполняется и для
функции
![]() .
.
Согласно с формулой
(5), функция
определена и непрерывна в интервале
![]() (так как в этом интервале определена и
непрерывна функция
,
то определена и непрерывна сложная
функция
(так как в этом интервале определена и
непрерывна функция
,
то определена и непрерывна сложная
функция
![]() ).
Имеем
).
Имеем
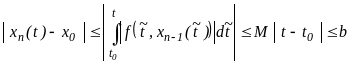
при
![]() .
Значит,
.
Значит,
![]() не выходит из
.
не выходит из
.
Покажем,
что последовательность
![]() равномерно
сходится в интервале
.
равномерно
сходится в интервале
.
Рассмотрим ряд
![]() (8)
(8)
Его частичные
суммы равны
![]() так что сходимость этого ряда эквивалентна
сходимости последовательности
.
так что сходимость этого ряда эквивалентна
сходимости последовательности
.
Из равенств (5) и (4) находим, что
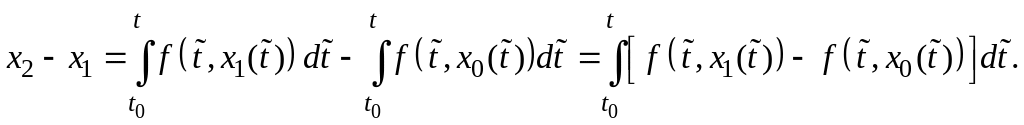
Отсюда
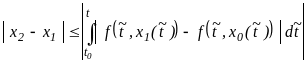 .
.
Считая, что
![]() и используя условие Липшица, получаем
и используя условие Липшица, получаем
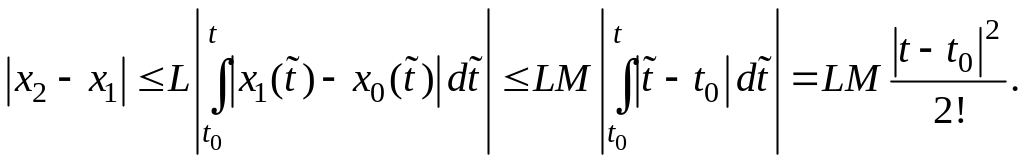
Допустим, что имеет место оценка
![]() .
(9)
.
(9)
Покажем, что тогда
![]() .
.
Действительно, имеем
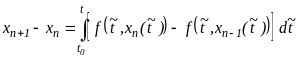 .
.
Отсюда
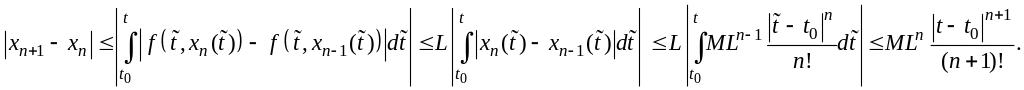 Так
как оценка (9) имеет место для
Так
как оценка (9) имеет место для
![]() и
и
![]() ,
то из вышесказанного и метода математической
индукции следует ее справедливость при
любом
.
Из (9) имеем
,
то из вышесказанного и метода математической
индукции следует ее справедливость при
любом
.
Из (9) имеем
![]() .
.
Согласно этой
формуле можно утверждать, что модули
членов ряда (8) не больше соответствующих
членов сходящегося ряда с положительными
членами:
![]() Согласно признаку Вейерштрасса
ряд (8) сходится и при том равномерно на
промежутке
.
А значит, по теореме о непрерывности
суммы ряда функция
Согласно признаку Вейерштрасса
ряд (8) сходится и при том равномерно на
промежутке
.
А значит, по теореме о непрерывности
суммы ряда функция
![]() ,
как сумма ряда (8) или предельная функция
последовательности
,
как сумма ряда (8) или предельная функция
последовательности
![]() ,
будет непрерывной при
.
,
будет непрерывной при
.
Покажем, что предельная функция удовлетворяет условию
![]() при
при
![]() (10)
(10)
и инегральному уравнению (3).
Действительно, переходя к пределу в неравенстве (6), получим неравенство (10).
Чтобы показать, что предельная функция есть решение (3), отметим, что
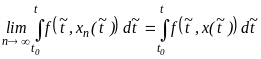 (11)
(11)
при . Действительно,
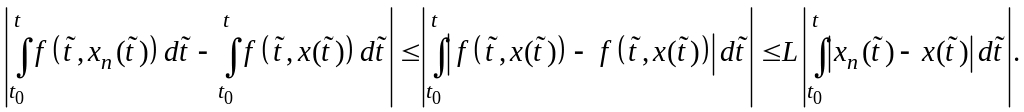
Так как
![]() сходится равномерно к
при
,
то для любого
сходится равномерно к
при
,
то для любого
![]() найдется номер
найдется номер
![]() такой, что при
такой, что при
![]() выполняется неравенство
выполняется неравенство
![]() для всех
из интервала
.
Поэтому
для всех
из интервала
.
Поэтому
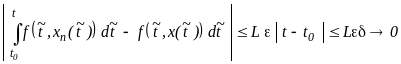 при
при
![]()
Таким
образом, соотношение (11) доказано.
Переходя в равенстве (5) к пределу при
![]() ,
получим (3). Значит,
—
непрерывное при
,
получим (3). Значит,
—
непрерывное при
![]() решение уравнения (3).
Оно представляет собой решение
дифференциального уравнения (1) с
начальным условием (2), определенное и
непрерывно дифференцируемо в интервале
.
решение уравнения (3).
Оно представляет собой решение
дифференциального уравнения (1) с
начальным условием (2), определенное и
непрерывно дифференцируемо в интервале
.
Докажем
теперь, что это решение единственно.
Допустим, что существует другое решение
![]() ,
удовлетворяющее тем же условиям (2),
определенное и непрерывное в некотром
интервале
,
удовлетворяющее тем же условиям (2),
определенное и непрерывное в некотром
интервале
![]() ,
где
,
где
![]() ,
и не выходит при таких
из области
.
Тогда при
будем иметь
,
и не выходит при таких
из области
.
Тогда при
будем иметь
 .
(12)
.
(12)
Оценим
разность
![]() .
Используя формулы (6), (12) и условием
Липшица, получим
.
Используя формулы (6), (12) и условием
Липшица, получим
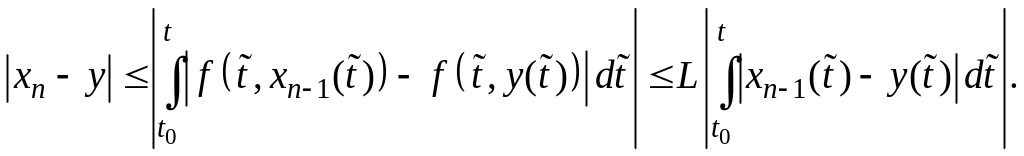 (13)
(13)
Из (12) имеем
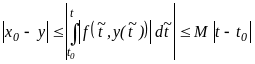 .
.
Учитывая это и допуская в (13) , получим
![]() (14)
(14)
Допуская
в (13)
![]() ,
с учетом (14) получаем
,
с учетом (14) получаем
![]()
Аналогично, далее получаем
![]() (15)
(15)
Правые
части неравенства (15) стремятся к нулю
при
(как общий член сходящегося ряда). Поэтому
![]() при
при
![]() Выше было доказано, что
Выше было доказано, что
![]() при
при
![]() Поэтому
Поэтому
![]() при
при
![]() ,
значит, решение
совпадает с решением
,
что и доказывает его единственность.
Теорема
доказана.
,
значит, решение
совпадает с решением
,
что и доказывает его единственность.
Теорема
доказана.
2. Дифференциальные уравнения с разделяющимися переменными. Уравнение
![]() ,
,
где
![]() – аргумент,
– аргумент,
![]() – искомая функция;
– искомая функция;
![]() и
и
![]() – заданные непрерывные в области
функции, называется дифференциальным
уравнением с разделяющимися переменными.
– заданные непрерывные в области
функции, называется дифференциальным
уравнением с разделяющимися переменными.
Разделив
это уравнение на
![]() ,
сведем его к уравнению
с разделенными переменными
,
сведем его к уравнению
с разделенными переменными
![]() ,
откуда
,
откуда
![]()
При таком
преобразовании можно потерять решения
![]() ,
где
,
где
![]() и
и
![]() ,
где
,
где
![]() .
Эти случаи нужно рассматривать отдельно.
Необходимо найти
.
Эти случаи нужно рассматривать отдельно.
Необходимо найти
![]() и
и
![]() такие, что
такие, что
![]() ,
,
![]() ,
и проверить, являются ли
,
и проверить, являются ли
![]() или
или
![]() решениями исходного
уравнения и содержатся ли они в общем
интеграле при каком-то
значении
решениями исходного
уравнения и содержатся ли они в общем
интеграле при каком-то
значении
![]() (соответственно
(соответственно
![]() ).
).
3. Однородные
дифференциальные уравнения первого
порядка. Функция
![]() называется однородной
функцией степени
называется однородной
функцией степени
![]() ,
если
,
если
![]() .
.
Уравнение вида
![]()
называется
однородным,
если![]() и
и
![]() однородные
функции одной и той же степени
.
однородные
функции одной и той же степени
.
Однородное уравнение может быть приведено к виду
![]() .
.
С помощью подстановки
![]() однородное уравнение приводится к
уравнению с разделяющимися переменными
относительно новой неизвестной функции
однородное уравнение приводится к
уравнению с разделяющимися переменными
относительно новой неизвестной функции
![]() .
.
Уравнения вида
![]()
при
![]() приводятся к однородным подстановкой
приводятся к однородным подстановкой
![]() где
где
![]() –
точка пересечения прямых
–
точка пересечения прямых
![]() и
и
![]()
Если
![]() ,
то подстановка
,
то подстановка
![]() при
при
![]() или
или
![]() при
при
![]() ,
,
![]() приводит данное уравнение к уравнению
с разделяющимися переменными.
приводит данное уравнение к уравнению
с разделяющимися переменными.
