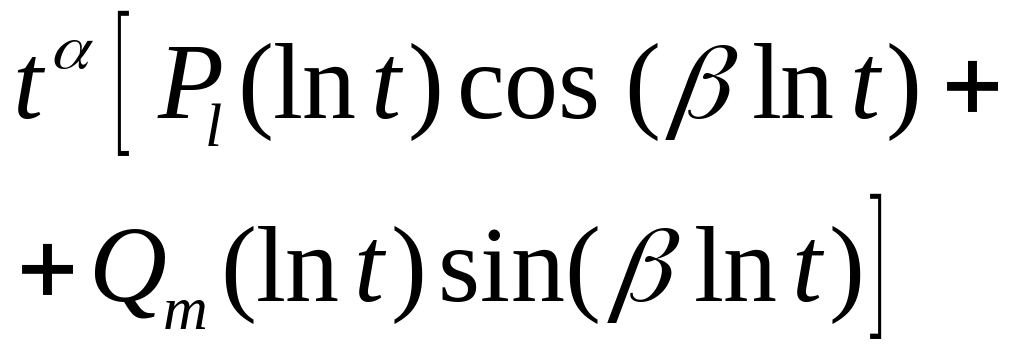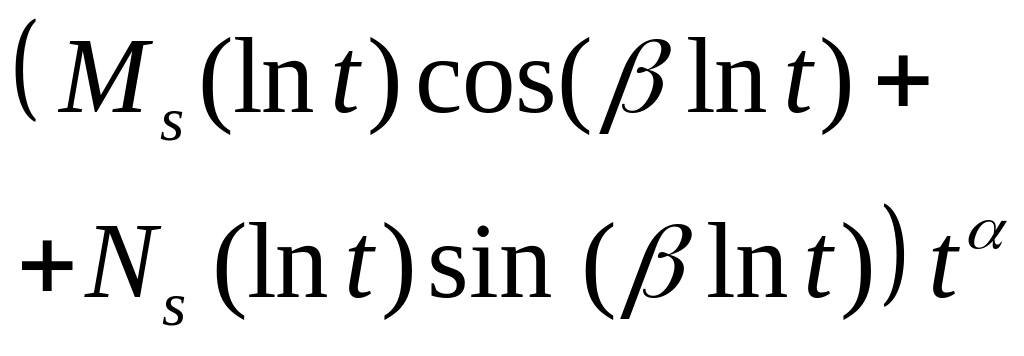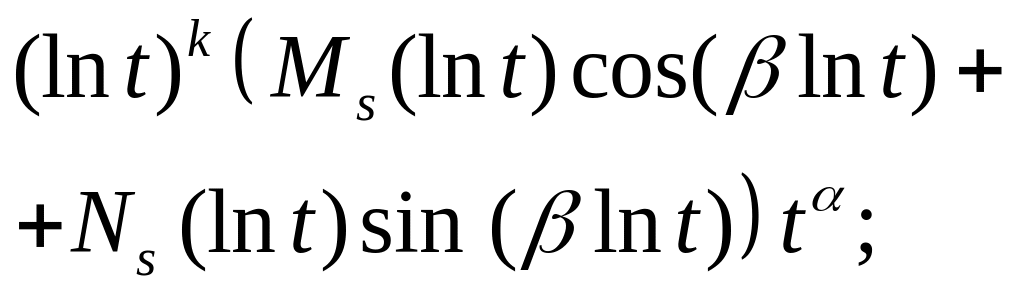Линейные уравнения и системы линейных дифференциальных уравнений с постоянными коэффициентами

§1. Линейные уравнения с постоянными коэффициентами

1. Линейные однородные уравнения с постоянными коэффициентами. Рассмотрим линейное однородное уравнение

(1)

где все коэффициенты постоянные действительные числа.

В силу общих свойств линейных уравнений, достаточно найти частных решений уравнения (1), образующих фундаментальную систему. Будем искать эти частные решения в виде (метод Эйлера)

(2)

Подставляя функцию (2) и ее производные в уравнение (1) после сокращения на , получим

(3)

Функция (2) будет удовлетворять уравнению (1), если число будет удовлетворять характеристическому уравнению (3).

Будем рассматривать случаи:

1⁰. Характеристическое уравнение (3) имеет различные действительные корни Согласно (2) этим корням будут соответствовать линейно независимые решения . Значит, общее решение уравнения (1) имеет вид где – произвольные постоянные.

2⁰. Среди корней уравнения (3) есть комплексный корень Так как действительные, то сопряженное число также будет его корнем. Тогда решениями уравнения (1) будут линейно независимые действительные функции , .

3⁰. Если – корень уравнения (3) кратности , то ему соответствуют линейно независимых решений уравнения (1).

4⁰. Каждой паре комплексно сопряженных корней кратности соответствуют частных решения уравнения (1): ..., EMBED Equation.2 ... ,

Схема решения уравнения (1):

1. Состваляем характеристическое уравнение (3).

2. Находим корни 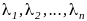уравнения (3).

3. Выписываем частные линейно независимые решения уравнения (1), согласно п. 1⁰ – 4⁰.

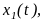
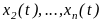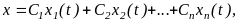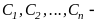4. Имея линейно независимых частных решения уравнения (1), получаем его общее решение где произвольные постоянные.

2. Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами. Рассмотрим линейное неоднородное уравнение -го порядка с постоянными коэффициентами

. (1)

Общее решение уравнения (1) определяется формулой где частное решение (1), ФСР соответствующего однородного уравнения.

Решение уравнения (1) можно найти:

1) методом вариации постоянных (метод принадлежит Лагранжу): допустим, ФСР соответствующего однородного уравнения, тогда общее решение этого уравнения имеет вид

, (2)

где произвольные постоянные. Решение уравнения (1) будем искать в предположении, что являются не константами, а функциями от , то есть в виде

, (3)

где гладкие функции, .

Уравнения для нахождения неизвестных имеют вид

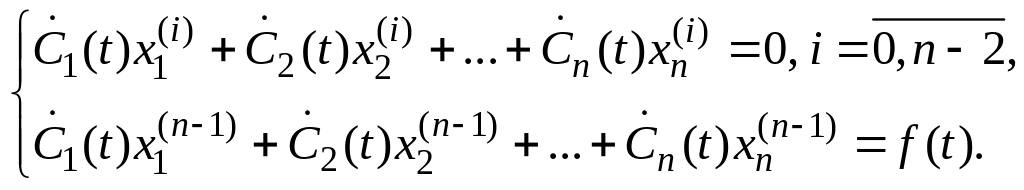
Так как ФСР однородного уравнения, то вронскиан . Поэтому эта система имеет единственное решение , подставив которое в формулу (3) получим общее решение линейного неоднородного уравнения (1) .

2) в случаях, когда правая часть (1) имеет специальный вид, частные решения находят методом неопределенных коэффициентов (методом подбора).

Таблица частных решений для различных видов правой части уравнения (1).

№№		Корни характеристичес-кого уравнения	Виды частного решения
10.		а) число – не корень
		б) число – корень кратности
20.		а) числа – не корни
		б) числа – корни кратности	.

3. Уравнение Эйлера. Уравнение вида

, (1)

где называется однородным уравнением Эйлера. Решают:

1. с помощью замены 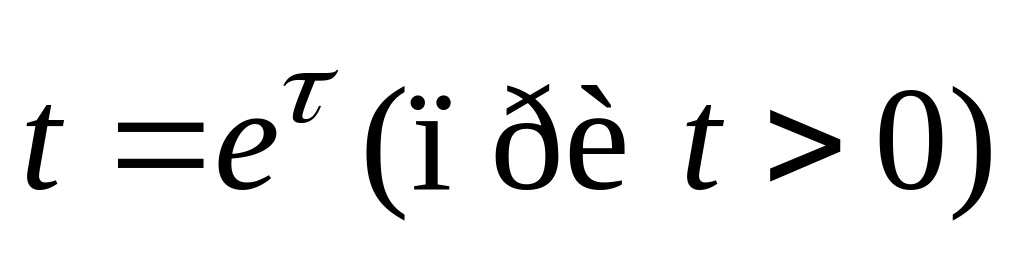уравнение приводится к линейному однородному уравнению с постоянными коэффициентами.

2. замена 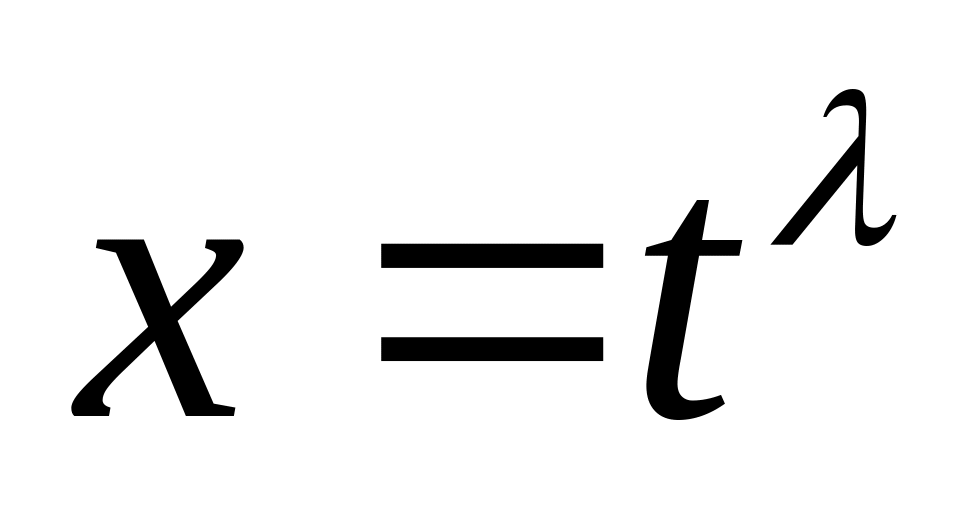. Подставляя в уравнение (1) имеем

(2)

Уравнение (2) называется характеристическим для уравнения (1).

1. Простому корню 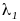уравнения (1) соответствует решение ;

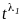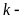2. кратному корню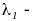 линейно независимых решений , , ,..., ;

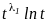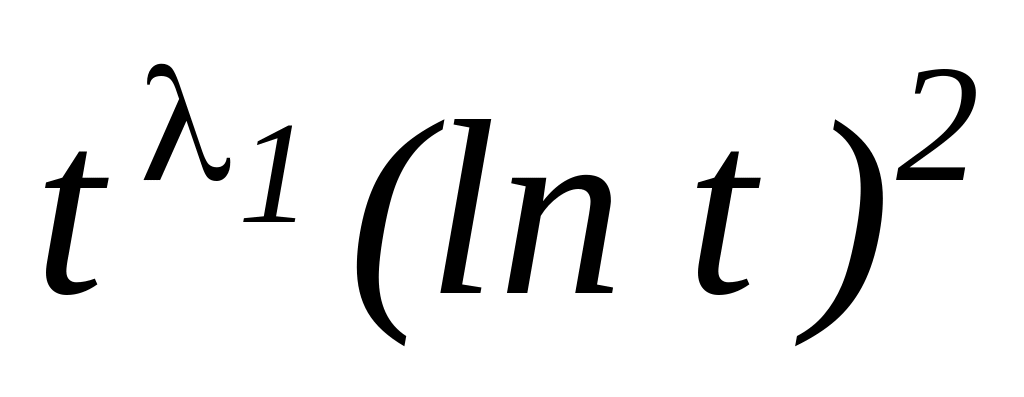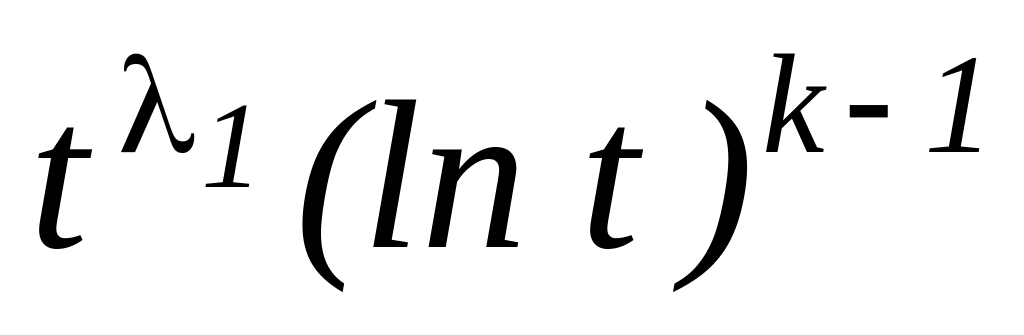3. Если коэффицтенты уранения действительные числа, а характеристическое уравнение имеет комплексно-сопряженные корни 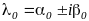кратности , то уравнение Эйлера имеет 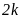линейно независимых решения

Неоднородное уравнение Эйлера

указанной выше подстановкой приводится к неоднородному уравнению с постоянными коэффициентами. При этом, если , где полином, то частное решение данного уравнения можно найти методом неопределенных коэффициентов.

Таблица частных решений для различных видов правой части уравнения (1).

№№		Корни характеристического уравнения	Виды частного решения
10.		а) число – не корень
		б) число – корень кратности
20.		а) числа – не корни
		б) числа – корни кратности	.

Прыклад 1.

Рашэнне. Характарыстычнае ўраўненне ці мае карані . Таму агульнае рашэнне адпаведнага аднароднага ўраўнення будзе мець выгляд

.

Частковае рашэнне адшукваецца ў выглядзе . Маем . Падстаўляючы ў дадзенае ўраўненне, атрымліваем

або адкуль Такім чынам, Агульным рашэннем будзе