1.Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.

P(AB)=P(A)PA(B)

Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2, ..., ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий,из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из N возможных результатов испытания. Это дает

;; Таким образом,

Следствия:

1.В случае независимости событий A к B формула (4) примет более простой вид:

2.PA(B)= P(AB)/P(A)

3.Если А независит от В, то В независит от А

4.Из независимости событий А И В: неА и неВ тоже независимы, и неА и В, А и неВ.

2. Теорема суммы Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Р(А+В)=Р(А)+Р(В)-Р(АВ)

Докажем теорему сложения для схемы случаев. Пусть п – число возможных исходов опыта, т_А – число исходов, благоприятных событию А, т_В – число исходов, благопри-ятных событию В, а т_АВ – число исходов опыта, при которых происходят оба события (то есть исходов, благоприятных произведению АВ). Тогда число исходов, при которых имеет место событие А + В, равно т_А + т_В – т_АВ (так как в сумме (т_А + т_В)  т_АВ  учтено дважды: как исходы, благоприятные А, и исходы, благоприятные В). Следовательно, вероятность суммы можно определить по формуле (1.1): Следствия:

1.P(A+B)=P(A)+P(B), если события несовместимы

2.P(A1)+P(A2)+…+P(An)=1

3.Р(А)+Р(А)=1

4.P(A1+A2+…+An)= 1 – P(A1+A2+…+An)

3.    Полная вероятность Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,

 Применяя аксиому сложения вероятностей, имеем

   Но (i=1, 2, ..., n), поэтому

4. Формула Байеса.  Допустим событие А может наступить только вмести з хотя бы одной из событий-гипотез Н1, Н2,…Нn, которые образуют полную группу. Если событие А настала, то условные гипотезы равны:, или

Доказательство: расматрим событие Ані и воспользуемся теоремой умножения:

Отсюда:

Но по формуле полной вероятности

   Поэтому

5. Формула Бернулли. Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить некоторое событие A. Пусть при каждом испытании вероятность наступления события А равна P(A)=p и, следовательно, вероятность противоположного события (ненаступления А) равна .

Вероятность Pn(m) того, что событие А произойдет m раз при n испытаниях:

так как: то:

.

Доказательство:

Всякую комбинацию, в которую А входит m раз и входит n-m раз, назовем благоприятной. Количество благоприятных комбинаций равно количеству k способов, которыми можно выбрать m чисел из данных n; таким образом, оно равно числу сочетаний из n элементов по m, т.е.

Подсчитаем вероятности благоприятных комбинаций. Рассмотрим сначала случай, когда событие A происходит в первых m испытаниях и, следовательно, не происходит в остальных n-m испытаниях. Такая благоприятная комбинация имеет следующий вид:

  Вероятность этой комбинации в силу независимости испытаний (на основании теоремы умножения вероятностей) составляет

Так как в любой другой благоприятной комбинации Вi событие A встречается также m раз, а событие происходит n-m раз, то вероятность каждой из таких комбинаций также равна . Итак

Все благоприятные комбинации являются, очевидно, несовместными. Поэтому (на основании аксиомы сложения вероятностей) Дискретная случайная величина X имеет биномиальный закон распределения, если она принимает значения 0, 1, 2, ..., m, ..., n с вероятностями где 0<p<1, q=1-p, m=0, 1, 2, ..., n. Биномиальный закон распределения представляет собой закон распределения числа X=m наступлений события A в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p.

6.Наивероятнейшаячастота. Число x появления события A в n повторных независимых испытаниях называется частотой.

вероятность этой частоты не меньше вероятности "предыдущей" и "последующей" частот:P_n(x)  P_n (x – 1);

P_n(x)  P_n (x+1) (*)

Первое неравенство (*) представляется в виде:

,

что эквивалентно или.

Отсюда следует:

Если np + p – целое число (тогда и np – q – целое число), то две частоты: x=np – q и x=np + p обладают наибольшей вероятностью. Например, при n = 7, p = 0,5 наивероятнейшие частоты: x = 3; x = 4

.7. Формула Пуассона. Распределение Пуассона получается как предельный случай распределения Бернулли, если устремить р к нулю, а n к бесконечности, но так, чтобы их произведение оставалось постоянным: nр = а. Формально такой предельный переход приводит к формуле Параметр распределения: a Пусть случайная величина X=m может принимать любое целое неотрицательное значение, причем , (m=0,1,2…n,…)    где a — некоторая положительная постоянная. В этом случае говорят, что случайная величина X распределена по закону Пуассона( закон рідкісних подій). Заметим, что при m=0 следует положить 0!=1.

8. Мат ожидание, дисперсия, и среднее квадратич. отклонение частоты и частости. Рассмотрим случайные величины Х_i=m_і i=1.2….n – частота появления события А. Закон распределения всех этих СВ:

Х_i=m_і 0 1

P q p

M(m_i)=p, а D(m_i)=p-p²=pq. Или M(m)=np, а D(m)=npq.

Для частости: M(m/n)=p, а D(m/n)==pq/n.

Математическим ожиданием дискретной случайной величины называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е. *

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математичекого ожидания *:

Средним квадратическим отклонением случайной величины называется корень квадратный из ее дисперсии:

9. Мат ожидание. Математическим ожиданием дискретной случайной величины называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е. *

1.Математическое ожидание постоянной С равно этой постоянной.   Дово. Постоянную C можно рассматривать как случайную величину , которая может принимать только одно значение C c вероятностью равной единице. Поэтому  2.Постоянный множитель можно выносить за знак математического ожидания, т.е.

Док-во. Используя соотношение (39), имеем

 3.Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:

4.Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин **:

5. M[X-M(X)]=0

10. Дисперсия. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математичекого ожидания *:

1. Дисперсия постоянной равна нулю. Доказательство. Пусть . По формуле (46) имеем

   так как математическое ожидание постоянной есть эта постоянная:

  2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

 Доказательство. На основании соотношения (46), можно записать

   Так как

   и

   то

 3.Если и - независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий:

4. Для вычисления дисперсии удобно использовать формулу: Dx = Mx² - (Mx)² 5. Если случайные величины Х и Y зависимы, то D(X+/-Y)= D(x)+D(y)+/-2cov(X, Y),Cov(X, Y)= M[(X-M(X))(Y- M(Y))]=M(XY)-M(X)M(Y) 6.Дисперсия произведения независимых случайных величин равна: D(XY)= M(X²)M(Y²)-M²(X)M²(Y) 7.Дисперсия среднего арифметического независимых случайных величин равна:D(X1+X2+…+Xn/n)=D(X1)+D(X2)+…D(Xn)/n²

11. Метод моментов. Пусть значение х_і ДСВ Х задачи с равномерным шагом h=x_i-x_i-1. Выбирая так называемый «условный ноль» Хо=х_k (близкий к среднему арифметическому), рассматриваем вспомогательную СВ U=(X-Xo)/h, котрая принимает целые значения 0,+-1,+-2,… Числовые характеристики исходной и спромогательной СВ связаны так: М(Х)=Хо+hM(U),D(X)=h²D(U), σ(X)=hσ(U).Доказательство: M(U)=M((X-Xo)/h)= (M(X)-M(Xo))/h= (M(X)-Xo)/h. Следовательно М(Х)=Хо+hM(U)/ Для дисперсии D(U)= D((X-Xo)/h²)=(D(X)+D(Xo))/h^2? Следовательно D(X)=h²D(U).

12.  Интергральной функцией распределения F(x) случйной величины Х называется функция, которая для каждого значения Х определяет вероятность того, что случайная величина примит значение, меньшее от числа х, т.е. F(x)=P(X<x)=P(-∞<X<x) Свойства интегральной функции распределения: 1. ,при чем 2. функція неспадна. От сюда: 3. Вероятность того, что непрерывная случайная величина Х примит отдельное значение равна 0, т.е. Р(Х=х1)=0.

13.Дифференциальная ф-ция и её св-ваДиф. функцией распределения наз. производная(если она существует)от интегральной ф-ции.F(x)=F’(x)

Св-ва

1)Это неотрицательная ф-ция f([)>=0

2)Вероятность того,что НВВ приймет значение из промежутка (a;b)находится по формуле

P(a<x<b)=∫a f(x)dx

P(a<x<b)=F(b)-F(a)=F(x)|ab=∫f(x)dx

3)Интегр. И диф. Ф-ции-эквивалентные обобщённые характеристики НВВ, которые связаны соотношением F(x)=∫f(t)dt

4)Условие формирования закона НВВ имеет вид ∫f(x)dx=1

14. Равномерное распределение

Непрерывная случайная величина имеет равномерное распределение на отрезке [a,b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю, т.е.

где С = Const. Используя условие нормировки 2 из § 9, определим С.

,

откуда с = 1/(b-a) и, следовательно, плотность равномерного распределения имеет вид:

Теперь определим вид интегральной функции распределения для этого закона, который в силу (9.1) будет следующим:

(14.2)

 

Изобразим графики f(x) и F(x):

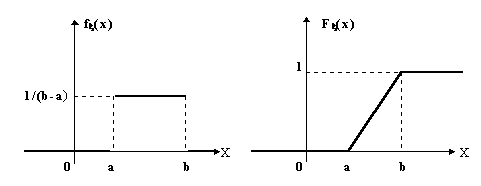
Определим числовые характеристики данной случайной величины:

Непрерывная случайная величина подчинена равномерному закону распределения, если ее возможные значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все значения случайной величины одинаково вероятны (обладают одной и той же плотностью вероятности).

15. Показательное распределение

В практических приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике, биологии, теории надежности, часто имеют дело со случайными величинами, которые имеют показательное распределение.

Случайная величина распределена по показательному закону с параметром  >0, если она непрерывна и имеет следующую плотность распределения вероятностей:

Тогда

(x > 0). соответственно, графики f(x) и F(x) имеют вид:

Определим числовые характеристики:

σ=М(x)=1/λ

D(x)=1/λ^2

16. Нормальное распределение

Непрерывная случайная величина имеет нормальное распределение вероятностей с параметрами а,  > 0, если плотность распределения ее имеет вид:

Нормальный закон распределения широко применяется в практических задачах, он проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. Каждый фактор в отдельности на величину  влияет незначительно.

M(x) = a.

D(x) =  ²

Таким образом, параметры а,  ² в выражении есть математическое ожидание и дисперсия нормально распределенной случайной величины, а График плотности вероятности имеет вид нормальной кривой (Гаусса):

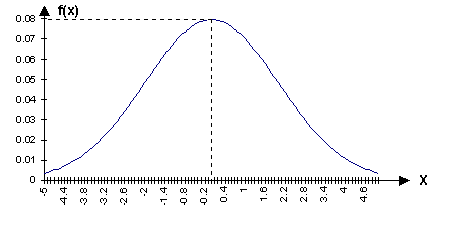
Отметим некоторые свойства нормальной кривой.

1. Кривая распределения симметрична относительно прямой х = а.

2.

3.

4. При изменении математического ожидания и при  = Const, происходит смещение кривой вдоль оси Ох. Если положить а = Const и изменять , то кривая изменяет свой вид в зависимости от  .

1.Фунция определена и непрерывна на всей числовой оси.2.Функция только положительная.

Вероятность попадания НВВ х в промежуток [x1;x2] находится по формуле

Р(x1<=X<=x2)=Ф(x2-a/σ)-Ф(x1-a/σ)

F(x)=0.5+Ф((x-a)/)