
- •1.Основные Законы геометрической оптики.
- •2.Тонкие сферические линзы. Формула тонкой линзы, построение изображений в линзах.
- •4.Дисперсия световых волн
- •6. Рассчитать интерференционную картину от 2-х источников.
- •7. Интерференция в тонких пленках
- •8.Использование интерференции
- •9. Дифракция света. Метод зон Френеля. Дифракция Френеля на круглом отверстии.
- •10. Дифракция Фраунгофера на щели. Условие максимума и минимума.
- •12.Поляризация света
- •13.Получение ПлоскоПоляризованного.
- •15. Анализ Поляризационного света. Закон Малюса.
- •16,Применение явлений поляризации
- •17. Тепловое излучение. Закон Кирхгофа.
- •18. Тепловое излучение. Закон Стефана-Больцмана. Законы Вина.
- •19. Излучение ачт – Смотрите 20
- •20. Излучение ачт гипотеза планка. Объяснение явления теплового излучения
- •21. Фотоэффект. Законы внешнего фотоэффекта.
- •4 Закона фотоэффекта
- •22. Квантовая теория фотоэффекта Уравнение Эйнштейна для фотоэффекта
- •23.Применение явления фотоэффекта
- •24. Эффект Комптона.
- •25. Квантовая теория давление света
- •26.Дискретностьфизических величин. Опыт франка герца
- •27. Дифракция электронов. Гипотеза Луи де Бройля.
- •30. Уравнение Шредингера.
- •31,Опыты Резерфорда классическая модель атома резенфорда
- •32. Постулаты Бора.
- •33. Квантовая теория атомаов. Квантовые числа. Принцип Паули.
32. Постулаты Бора.
Для того, чтобы объяснить линейчатые спектры атомов датский физик Нильс Бор в 1913 году вводит два постулата.
Первый
постулат Бора
(постулат стационарных состояний): в
атоме существуют стационарные (не
изменяющиеся во времени) состояния, в
которых он не излучает энергию. Энергии
этих состояний образуют дискретный
ряд:
 ,
,
 ,
…,
,
…,
 .
Стационарным состояниям атома
соответствуют орбиты, по которым
движутся электроны. Хотя электроны
движутся по стационарным орбитам с
ускорением, они не излучают и не поглощают
энергию.
.
Стационарным состояниям атома
соответствуют орбиты, по которым
движутся электроны. Хотя электроны
движутся по стационарным орбитам с
ускорением, они не излучают и не поглощают
энергию.
В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные значения момента импульса, удовлетворяющие условию:
 ,
n=1,
2, 3,…, где
,
n=1,
2, 3,…, где
 - масса электрона,
- масса электрона,
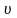 - его скорость по n-ой
орбите радиуса
- его скорость по n-ой
орбите радиуса
 ,
.
,
.
Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) квант с энергией:
 .
.
При
 происходит излучение фотона (переход
из состояния с большей энергией в
состояние с меньшей энергией), при
происходит излучение фотона (переход
из состояния с большей энергией в
состояние с меньшей энергией), при
 - поглощение фотона (переход атома в
состояние с большей энергией).
- поглощение фотона (переход атома в
состояние с большей энергией).
Набор
возможных дискретных частот
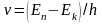 определяет линейчатый спектр атома.
определяет линейчатый спектр атома.
33. Квантовая теория атомаов. Квантовые числа. Принцип Паули.
Собственные
функции
 ,
являющиеся решениями уравнения
Шредингера зависят от трех квантовых
чисел: n,
и
.
n
- главное квантовое число, определяет
энергетические уровни электрона в
атоме и принимает значения n
= 1, 2, 3,…
,
являющиеся решениями уравнения
Шредингера зависят от трех квантовых
чисел: n,
и
.
n
- главное квантовое число, определяет
энергетические уровни электрона в
атоме и принимает значения n
= 1, 2, 3,…
- орбитальное квантовое число, оно связано с квантованием момента импульса электрона (механического орбитального момента). То есть орбитальный момент не может быть произвольным, а принимает дискретные значения, определяемые формулой:
|
(1) |
При данном значении n - принимает значения
|
Всего n значений.
m - магнитное квантовое число, связанное с квантованием проекции момента импульса на выбранное направление (обычно в направлении магнитного поля по оси z):
|
(2) |
Магнитное квантовое число может принимать следующие значения:
m=0,
|
Всего
 значений.
значений.
Принцип
Паули - в
одном и том же атоме не может быть двух
электронов с одинаковыми квантовыми
числами
,
,
,
 .
То есть два электрона должны отличаться
по крайней мере значениями одного
квантового числа.
.
То есть два электрона должны отличаться
по крайней мере значениями одного
квантового числа.
Состояние каждого электрона в атоме характеризуется четырьмя квантовыми числами:
(n = 1, 2, 3,…) – квантует энергию ,
(
0,
1, 2,…,
 )
– квантует орбитальный механический
момент
)
– квантует орбитальный механический
момент
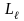 ,
,
(m
= 0,
,
,…,
)
– квантует проекцию момента импульса
на заданное направление

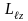 ,
,
(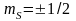 )
– квантует проекцию спина на заданное
направление
)
– квантует проекцию спина на заданное
направление
 .
С возрастанием
растет энергия. В нормальном состоянии
атома электроны находятся на самых
низких энергетических уровнях.
.
С возрастанием
растет энергия. В нормальном состоянии
атома электроны находятся на самых
низких энергетических уровнях.


 0,1,
2,…, n-1.
0,1,
2,…, n-1.
 ,
,
 ,…,
,…,
