
- •1.Основные Законы геометрической оптики.
- •2.Тонкие сферические линзы. Формула тонкой линзы, построение изображений в линзах.
- •6. Рассчитать интерференционную картину от 2-х источников.
- •7. Интерференция в тонких пленках
- •9. Дифракция света. Метод зон Френеля. Дифракция Френеля на круглом отверстии.
- •10. Дифракция Фраунгофера на щели. Условие максимума и минимума.
- •14. Поляризация света. Закон Малюса.
- •15. Анализ Поляризационного света. Закон Малюса.
- •17. Тепловое излучение. Закон Кирхгофа.
- •18. Тепловое излучение. Закон Стефана-Больцмана. Законы Вина.
- •21. Фотоэффект. Законы внешнего фотоэффекта.
- •22. Квантовая теория фотоэффекта Уравнение Эйнштейна для фотоэффекта
- •24. Эффект Комптона.
- •27. Дифракция электронов. Гипотеза Луи де Бройля.
- •30. Уравнение Шредингера.
- •32. Постулаты Бора.
- •33. Квантовая теория атомаов. Квантовые числа. Принцип Паули.
10. Дифракция Фраунгофера на щели. Условие максимума и минимума.
П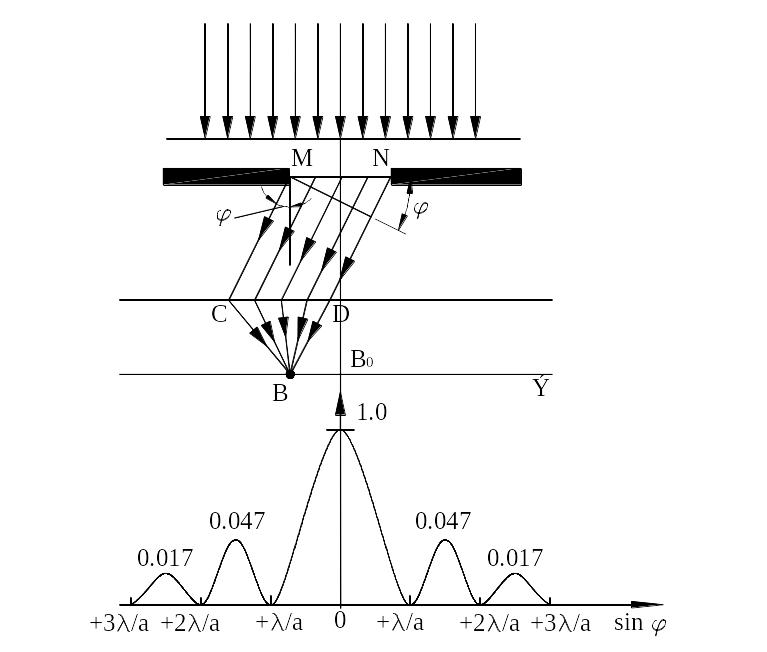 усть
на щель шириной
усть
на щель шириной
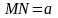 падает монохроматический свет с длиной
волны
падает монохроматический свет с длиной
волны
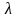 .
Из-за дифракции свет после щели
распространяется во всех направлениях.
Лучи, которые идут не отклоняясь,
собираются линзой в точке D
(экран находится
в фокальной плоскости линзы). Точка D
- главный фокус линзы. Рассмотрим лучи,
которые дифрагируют под углом
.
Из-за дифракции свет после щели
распространяется во всех направлениях.
Лучи, которые идут не отклоняясь,
собираются линзой в точке D
(экран находится
в фокальной плоскости линзы). Точка D
- главный фокус линзы. Рассмотрим лучи,
которые дифрагируют под углом
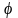 .
Они соберутся на экране в некоторой
точке B
(побочном фокусе линзы). Лучи, дифрагирующие
под другими углами, соберутся в других
точках на экране. В итоге экран будет
освещен во многих местах, на нем будет
чередование света и тени. Окажется в
точке B
минимум или максимум зависит от разности
хода поступающих сюда волн. Щель является
волновой поверхностью. По принципу
Гюйгенса каждая точка ее есть источник
вторичных волн. Найдем разность хода
волн, приходящих в точку B.
Для этого проведем фронт волны BD.
Точный расчет показывает, что оптические
пути MB
и FB
одинаковы (геометрически путь FB
короче, но здесь толще линза). Поэтому
разность хода лучей 1 и 2 равна
.
Они соберутся на экране в некоторой
точке B
(побочном фокусе линзы). Лучи, дифрагирующие
под другими углами, соберутся в других
точках на экране. В итоге экран будет
освещен во многих местах, на нем будет
чередование света и тени. Окажется в
точке B
минимум или максимум зависит от разности
хода поступающих сюда волн. Щель является
волновой поверхностью. По принципу
Гюйгенса каждая точка ее есть источник
вторичных волн. Найдем разность хода
волн, приходящих в точку B.
Для этого проведем фронт волны BD.
Точный расчет показывает, что оптические
пути MB
и FB
одинаковы (геометрически путь FB
короче, но здесь толще линза). Поэтому
разность хода лучей 1 и 2 равна
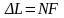 .
Проведем систему плоскостей параллельных
MF
на расстоянии
друг от друга. Разность хода разделиться
на участки длиной
,
а щель на полоски, называемые зонами
Френеля.
.
Проведем систему плоскостей параллельных
MF
на расстоянии
друг от друга. Разность хода разделиться
на участки длиной
,
а щель на полоски, называемые зонами
Френеля.
Площади этих зон одинаковы, поэтому по принципу Гюйгенса-Френеля они испускают волны равной интенсивности. Разность хода между соответствующими точками соседних полосок по построению равна . Поэтому, если в щели укладывается четное число зон Френеля, они попарно друг друга погасят. Тогда в точке B будет наблюдаться минимум, если нечетное, то одна зона окажется непогашенной и в точке B будет максимум.
Число
зон Френеля равно
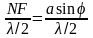 .
Если это число четное, то мы получаем
условие минимума:
.
Если это число четное, то мы получаем
условие минимума: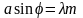 ,
,
если
нечетное, то условие максимума: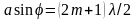 .
.
14. Поляризация света. Закон Малюса.
Доказательством поперечности световых волн является явление поляризации света.
Световая волна состоит из множества цугов, испускаемых большим числом атомов. Каждый цуг имеет случайную ориентацию векторов E и H, в итоге в результирующей волне все направления равновероятны. Свет со всевозможными равновероятными направлениями векторов E и H называется естественным (скорость распространения направлена перпендикулярно чертежу).
Свет,
в котором одно из направлений колебаний
светового вектора
 становится преимущественным, называется
частично поляризованным
становится преимущественным, называется
частично поляризованным
![]()
Е![]() сли
колебания светового вектора происходят
в одной плоскости, то свет –
плоско-поляризован.
сли
колебания светового вектора происходят
в одной плоскости, то свет –
плоско-поляризован.
Если конец вектора описывает эллипс, то свет эллиптически поляризован, если окружность, то поляризован по кругу.
Закон
Малюса:
Интенсивность прошедшего света равна
интенсивности падающего света на угол
между плоскостью колебаний падающего
света и плоскостью поляризатора.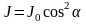 .
.
Поставим
на пути естественного света два
поляризатора, плоскости которых
составляют угол
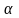 .
Из первого поляризатора выйдет
плоско-поляризованный свет, интенсивность
которого
.
Из первого поляризатора выйдет
плоско-поляризованный свет, интенсивность
которого
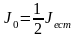 .
Согласно закону Малюса из второго
поляризатора выйдет свет интенсивности
.
Интенсивность света, прошедшего второй
поляризатор равна:
.
Согласно закону Малюса из второго
поляризатора выйдет свет интенсивности
.
Интенсивность света, прошедшего второй
поляризатор равна: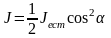 .
.
Максимальная
интенсивность, равная
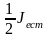 получается при
получается при
 (поляризаторы параллельны). При
(поляризаторы параллельны). При
 интенсивность равна нулю (скрещенные
поляризаторы света не пропускают).
интенсивность равна нулю (скрещенные
поляризаторы света не пропускают).
