Вопрос 17:Алгоритмы численного решения нелинейных уравнений;метод Ньюютона,метод половинного деления,метод хорд.

Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:

отделение корней, - т.е. определение интервалов изоляции [a,b], внутри которого лежит каждый корень уравнения;

уточнение корней, - т.е. сужение интервала [a,b] до величины равной заданной степени точности .

Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:

метод половинного деления (метод дихотомии);

метод простых итераций ;

метод Ньютона (метод касательных) ;

модифицированный метод Ньютона ( метод секущих );

метод хорд и др.

Метод Ньютона для нелинейного уравнения.

Для решения нелинейного уравнения f(x)=0 по методу Ньютона используется итерационный процесс:

x(k+1) = x(k) - f(x(k))/f '(x(k)) , k = 0, 1, 2, ... (2.15)

где x(0) - некоторое начальное приближение к корню.

При этом предполагается, что f '(x)≠ 0 на отрезке [a,b].

Геометрический вывод формулы.

Геометрически итерационный процесс метода Ньютона означает замену на k-той итерации графика функции y=f(x) на касательную к этой функции в точке (x(k) , f(x(k))) (в связи с этим метод также иногда называется методом касательных). Уравнение касательной имеет вид

y=f '(x(k))(x-x(k))+f(x(k)) Найдем точку пересечения с осью OX этой касательной (вместо функции y=f(x)), что соответствует нахождению решения линейного уравнения:

f '(x(k))(x-x(k))+ f(x(k))=0

вместо нелинейного f(x)=0.

Выражая x, получаем: x = x(k) - f(x(k))/f '(x(k))≡ x(k+1)

Аналитический вывод формулы.

Рассмотрим уравнение f(x)=0, X - его корень, x(k) - k-ое приближение к корню. Тогда по теореме Лагранжа о средних значениях имеем: 0 = f(X) = f(x(k)) + (X - x(k) )f '(ck ), где ck ∈ (X, x(k) ). Заменяя f '(ck) на значение f '(x(k) ) (то есть используя предыдущее приближение к корню) приходим к приближенному равенству 0 ≈ f(x(k)) + (X - x(k))f '(x(k)). Откуда получаем X ≈ x(k) - f(x(k))/f '(x(k)) ≡ x(k+1)

Сходимость метода Ньютона.

Для исследования сходимости метода Ньютона перепишем его в виде частного случая метода простой итерации, достаточные условия сходимости которого уже известны. Имеем:

x(k+1) = x(k) - f(x(k))/f '(x(k))

Следовательно,

x(k+1) = φ(x(k)), где φ(x) = x - f(x) / f '(x)

Проверим следующее условие теоремы о сходимости метода простой итерации:

|φ '(x)| ≤ q < 1. (2.16)

В случае метода Ньютона имеем:

φ '(x) = 1 - [(f '(x))2 - f ·f ''] / (f ')2 (2.17)

Пусть корень X уравнения f(x)=0 имеет кратность p ≥ 1. Тогда в достаточно малой окрестности корня X имеет место представление:

f(x) ≈ a(x-X) p

Следовательно

φ '(x) = f ·f ''/(f ') 2 ≈ a(x-X) pa·p(p-1)(x-X) p-2/[a·p(p-1)(x-X) p-1] 2 =

= (p-1)/p < 1

Таким образом в некоторой окрестности корня X условие (2.16) выполнено с константой q < 1.

ЗАМЕЧАНИЕ 2.3

1) Метод Ньютона является наиболее часто используемым для нахождения корней произвольной дифференцируемой функции, особенно если известны достаточно точные начальные приближения для корней.

2) При вычислении корня уравнения с точностью ε по методу Ньютона условием окончания итераций может служить:

| x(k+1) - x(k) | ≤ ε

Метод половинного деления

Его ещё называют методом дихотомии. Этот метод решения уравнений отличается от выше рассмотренных методов тем, что для него не требуется выполнения условия, что первая и вторая производная сохраняют знак на интервале [a, b]. Метод половинного деления сходится для любых непрерывных функций f(x) в том числе недифференцируемых.

Разделим отрезок [a, b] пополам точкой . Если (что практически наиболее вероятно), то возможны два случая: либо f(x) меняет знак на отрезке [a, c] (Рис. 3.8), либо на отрезке [c, b] (Рис. 3.9)

Рис. 3.8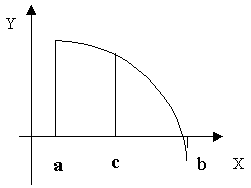

Рис. 3.9

Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

Метод хорд- итерационный численный метод приближённого нахождения корня алгебраического уравнения.

Пусть f(a)f(b)<0. Сущность метода (его еще называют методом ложного положения) состоит в замене кривой y=f(x) хордами, проходящими через концы отрезков, в которых f(x) имеет противоположные знаки. Метод хорд требует, чтобы один конец отрезка, на котором ищется корень, был неподвижен. В качестве неподвижного конца х0 выбирают тот конец отрезка, для которого знак f(x) совпадает со знаком второй производной . Расчетная формула имеет вид

Метод хорд является двухточечным, его сходимость монотонная и односторонняя.