27. Выпуклость, вогнутость. Точки перегиба.

Пусть f:XR дифференцируема в точке x0X. Будем говорить, что функция f выпукла вниз (вверх) в точке x0, если существует ε>0 такое, что для любого

Геометрически выпуклость вверх(вниз) означает, что в некоторой проколотой окрестности x0 график лежит выше (ниже) касательной к графику в точке x0.

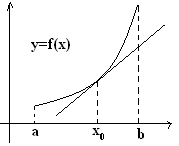
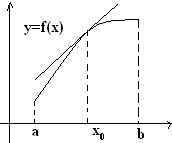
Е

сли f’’(x0)>0(<0), то функция f выпукла вниз (вверх) в точке x0.

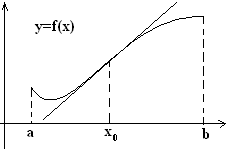
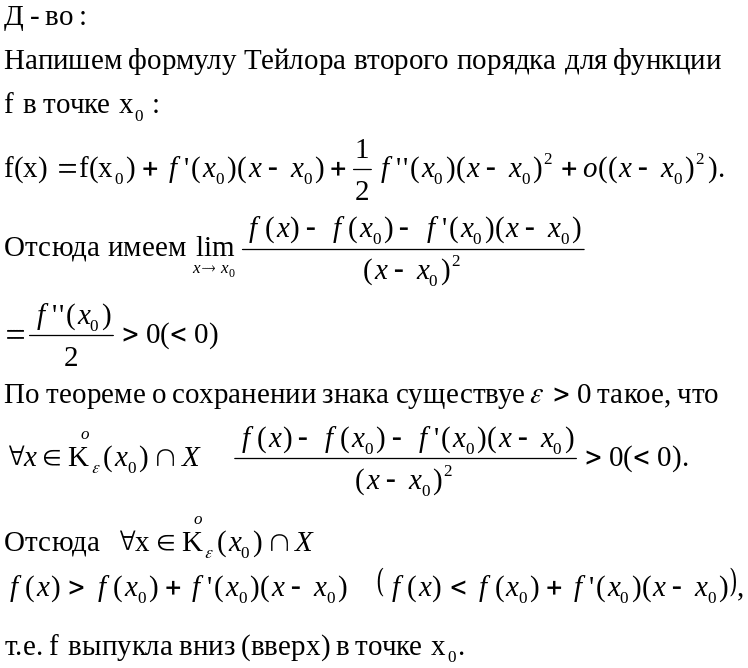
Точки, при переходе через которые характер выпуклости функции f меняются, называются точками перегиба функции.

Пусть x0 точка перегиба функции f. Если существует f”(x0), то f”(x0)=0.

Д-во:

Допустим, что f”(x0)>0(<). Тогда по теореме о выпуклости функция выпукла вниз (вверх) в точке x0, что противоречит условию. Следовательно f”(x0)=0.

Если при переходе через “подозрительную” точку x0 вторая производная меняет знак, то x0-точка перегиба. В противном случае перегиба нет.

28. Асимптоты графика функции.

26. Экстремум функции. Необходимые и достаточные условия.

Пусть f:XR, x0X предельная точка множества X. Если x0 предельная справа (на не слева) или x0 предельная слева (но не справа) иди f’(x0)=0, или f’(x0) не существует, то x0 называется критической точкой функции f.

По следствию из теоремы Ферма функция может иметь экстремум только в критических точках. Этот факт называют необходимым условием экстремума.

Достаточные условия существования экстремума. Теорема.

Пусть функция f непрерывна в точке x0, для некоторого ε>0 Kε(x0) и существует f’ в . Тогда:

1. Если f’>0 на (x0-ε,x0) и f’<0 на (x0,x0+ε), то x0-точка максимума.

2. Если f’<0 на (x0-ε,x0) и f’>0 на (x0,x0+ε), то x0-

точка минимума.

3. Если f’>0 (<0) на (x0-ε,x0)(x0,x0+ε), то в точке x0 экстремума нет.

Д-во:

1. По теореме о монотонности f возрастает на (x0-ε,x0) и убывает (x0,x0+ε), a потому для x

2. Аналогично 1-му.

3. По теореме о монотонности f возрастает (убывает) на (x0-ε,x0+ε), а пототму в точке x0 экстремума нет.

Критическая точка x0 функции f называется стационарной, если f’(x0)=0.

25. Условия монотонности и постоянства функции.

Функция f:[a,b]R непрерывна на [a,b] и дифференцируема во всех точках (a,b).

Теорема. 1) Функция f не убывает (не возрастает, постоянна) на [a,b]  f’≥0(≤0,=0) на (a,b); 2) Если f’>0(<0) на (a,b), то f возрастает (убывает) на [a,b].

21. Теорема Ферма.

Теорема Ферма:

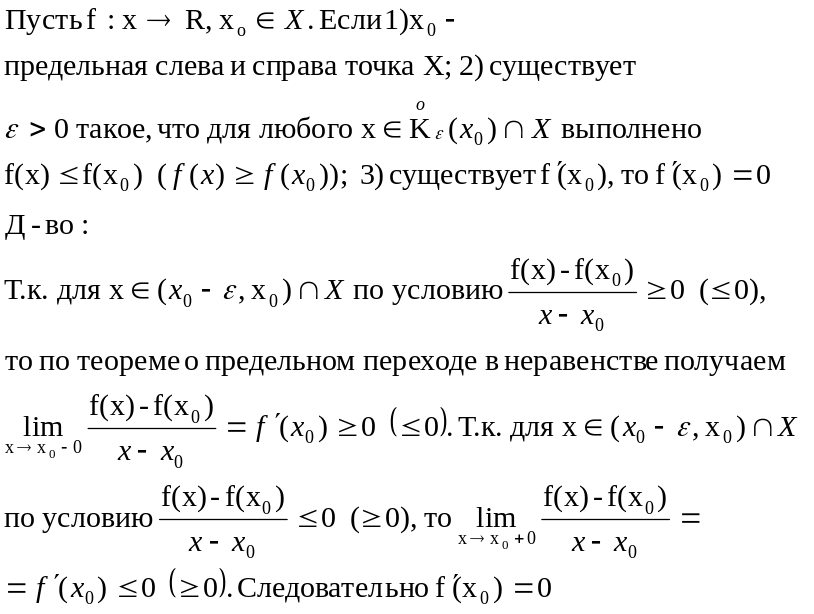Следствие: Если в точке x0, предельной слева и справа для множества Х, функция f достигает максимума (минимума) и существует f’(x0), то f’(x0)=0.

22. Теорема Ролля.

Теорема Ролля:

Пусть функция f:[a,b]→R непрерывна на [a,b] и дифференцируема в любой точке из [a,b]. Если f(a)=f(b), то существует точка x0(a,b) такая, что f’(x0)=0.

23. Теорема Лагранжа

Теорема Лагранжа:

Пусть функция f:[a,b]→R непрерывна на [a,b] и дифференцируема в любой точке из [a,b]. Тогда существует точка x0(a,b) такая, что f(b)-f(a)=f’(x0)(b-a) (Формула Лагранжа).

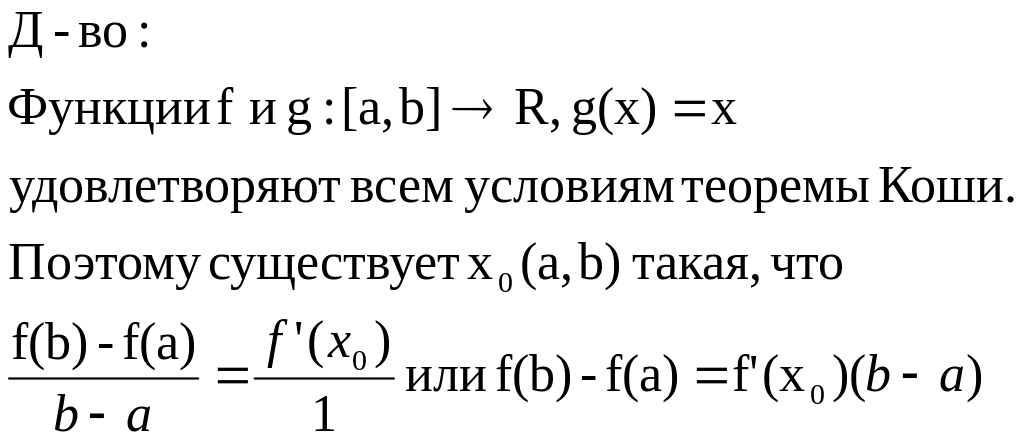
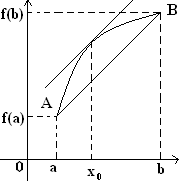
Теорема Лагранжа имеет простой геометрический смысл. Очевидно, что

(

f(b)-f(a))/(b-a) есть угловой коэффициент хорды [AB], а f’(x0) - угловой коэффициент касательной к графику функции f в точке x0. Теорема Л утверждает, что существует точка, в которой касательная параллельна хорде.

24. Теорема Лопиталя.

10. Непрерывность монотонной функции. Непрерывность основных элементарных функций.

Если значения монотонно возрастающей (убывающей) в промежутке X функции f(x) содержатся в промежутке Y и сплошь заполняют его (каждое значение y из Y принимается функцией хоть раз), то эта функция непрерывна в X.

Д-во:

Попробуем допустить, что в какой-нибудь точке x0 из X функция f(x) терпит разрыв, например, слева. Этот разрыв может быть только скачком. В этом случае существует предел f(x0-0), но он меньше значения f(x0). Так как для x< x0 будет f(x)≤f(x0-0), а для x> x0, очевидно f(x)≥f(x0), то функция не может принимать значений y, лежащих между числами f(x0-0) и f(x0), принадлежащими промежутку Y. Это противоречит условию теоремы. Значит, на деле функция f(x) разрывов не имеет.

Целая и дробная рациональные функции.

12. Непрерывность функции. Классификация точек разрыва.

Функция f(x), определенная в окрестности некоторой точки х₀, называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т.е.

Тот же факт можно записать иначе:

Если функция f(x) определена в некоторой окрестности точки х₀, но не является непрерывной в самой точке х₀, то она называется разрывной функцией, а точка х₀ – точкой разрыва.

Функция f(x) называется непрерывной в точке х₀, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию

верно неравенство .

Функция f(x) называется непрерывной в точке х = х₀, если приращение функции в точке х₀ является бесконечно малой величиной.

f(x) = f(x₀) + (x)

где (х) – бесконечно малая при хх₀.

Свойства непрерывных функций.

1) Сумма, разность и произведение непрерывных в точке х₀ функций – есть функция, непрерывная в точке х₀.

2) Частное двух непрерывных функций

– есть непрерывная функция при условии, что g(x) не равна нулю в точке х₀.

3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х₀, то функция v = g(f(x)) – тоже непрерывная функция в этой точке.

Точка разрыва а функции а называется: 1) точкой устранимого разрыва, если существует ; 2) Точкой разрыва первого рода, если существуют конечные, но ; 3) точкой разрыва второго рода, если она не является точкой разрыва первых двух типов, т.е. если хотя бы один из односторонних пределов либо не существует, либо бесконечен.

Сравнение предельного поведения функц. О-большое, о-малое. Эквивалентность.

Пусть а – предельная точка множества Ч, заданы функции f,g:X→R, причем g(x)≠0 в некоторой проколотой окрестности точки а.

1. Функция а есть о-малое от функции g при x→a, если . При это пишут: f(x)=o(g(x)) при x→a. Если f и g являются бесконечно малыми при x→a и f(x)=o(g(x)), то функция f называется бесконечно малой высшего порядка малости, чем g при x→a.

2. Функции f и g эквивалентны при x→a, если При этом пишут: f(x)~g(x) при x→a.

3. Функция f есть О-большое от функции g при x→a (f ограничена по сравнению с g при x→a), если в некоторой проколотой окрестности точки а для некоторого К>0 выполнено неравенство |f(x)|≤K|g(x)|. При этом пишут а(x)=O(g(x)) при x→a.

4. Предел суммы, произведения, частного.

1)

Д-во

Представим f(x) = A + (x), g(x) = B + (x), где , тогда

f(x)  g(x) = (A + B) + (x) + (x)

A + B = const, (х) + (х) – бесконечно малая, значит

2)

Д-во

Представим f(x) = A + (x), g(x) = B + (x), где , тогда

AB = const, (х) и (х) – бесконечно малые, значит

3)

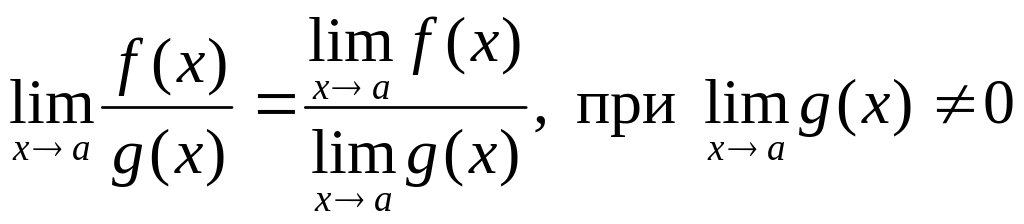
5. Предельный переход в равенстве и неравенстве.

Предельный переход в неравенстве.

Если и в некоторой проколотой окрестности точки a справедливо неравенство f(x)≤g(x), то b≤c.

Д-во:

Допустим противное b>c. Тогда и по теореме о сохранении знака в некоторой проколотой окрестности справедливо неравенство f(x)-g(x)>0. По условию в некоторой проклотой окрестности справедливо неравенство f(x)≤ g(x). Пусть . Тогда в должны быть справедливы оба неравенства, f(x)≤ g(x) и f(x)>g(x), что невозможно.

Предельный переход в равенстве.

Пусть существует окрестность такая, что для всех точек X верно f(x)=g(x), и при этом существует

6. Теорема о сжатой переменной

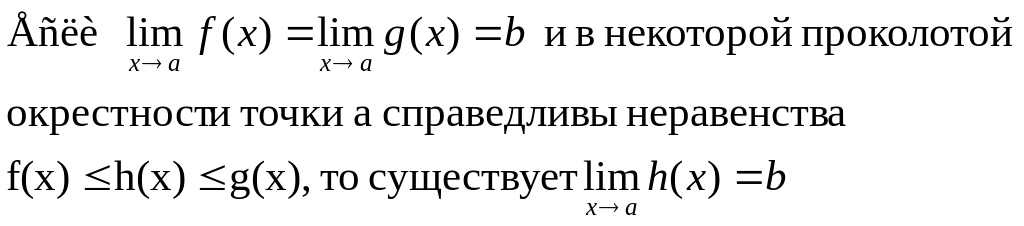
Д-во:

Возьмем произвольное ε>0.

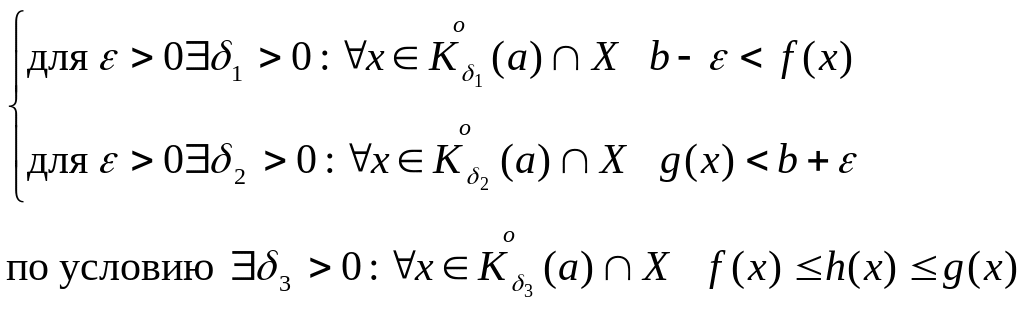
Возьмем . Тогда для

Справедливы все три утверждения:

По определению предела имеем

3. Предел функции. Бесконечно малые. Теорема о единственности предела и о сохранении знака.

Число А называется пределом функции f(x) при ха, если для любого >0 существует такое число >0, что для всех х таких, что 0 < x - a <  верно неравенство f(x) - A< .

Функция f(x) называется бесконечно малой при ха, где а может быть числом или одной из величин , + или -, если.

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет

Теорема о единственности предела: (10с.)

7 Первый замечательный предел.

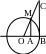. Док-во: возьмём

единичную окружность. Угол МОВ=х 0<x</2. площадь треугольника МОВ меньше, чем площадь сектора МОВ и меньше, чем площадь треугольника СОВ. |MA|=sin x, |CB|=tgx.

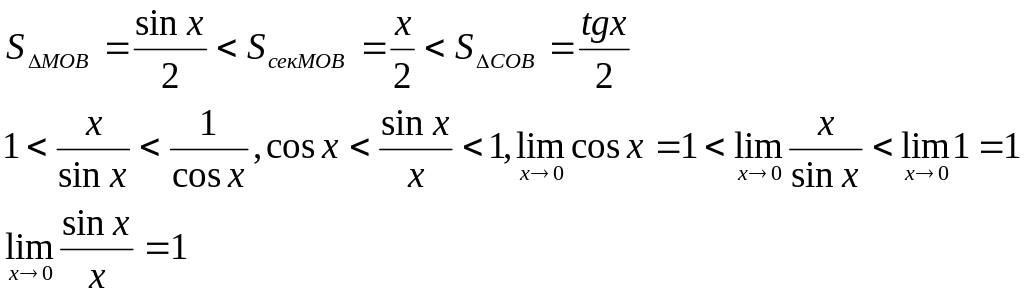по теореме о сжатой переменной.

Второй замечательный предел.

11, Свойства функций, непрерывных на отрезке (a;b)

Функция f(x) называется ограниченной на отрезке [a;b], если существует такое c=const, c>0, что модуль функции |f(x)|c для всех x[a;b], в противном случае функция называется неограниченной на отрезке.

Теорема: всякая непрерывная на отрезке [a;b] функция ограничена на отрезке [a;b]

Теорема Вейерштрасса: если функция непрерывна на [a;b], то она достигает на этом отрезке своего наибольшего и наименьшего значения.

Теорема: если функция непрерывна на [a;b] и на его концах принимает значения разных знаков, то внутри отрезка найдётся хотя бы одна точка с, значение функции в которой равно 0.

8. Сравнение бесконечно малых величин.

A(x)-б.м.ф., B(x)-б.м.ф. Если

1. , то б.м.ф. одного порядка.

2. , то А(х)-бесконечно малая более высокого порядка (более высокая степень малой), чем В(х).

3. , то А(х)-б.м.ф. более низкого порядка, чем В(х).

4. не существует, то А(х) и В(х) – несравнимы.

5. , то А(х) и В(х)-эквивалентные б.м.ф.

Теорема: предел функции не изменится, если под знаком предела одну б.м.ф. заменить на эквивалентную ей.

Основные эквивалентности, используемые при вычислении предела (всё при х0):

Sin x~x; tgx~x; arcsinx~x; arctgx~x; 1-cosx~x²/2; e^x-1~x; a^x-1~x*ln a; ln(1+x)~x; log_a(1+x)~x/lna

9. Непрерывность функций

.Непрерывность функции в точке

Пусть функция определена в некоторой окрестности точки х0, функция y=f(x) называется непрерывной в точке х0, если существует предел в этой точке и он равен значению функции в этой точке.

Замечание: для непрерывной функции можно переставить знак функции и предела, т.е.

х=х-х0 – приращение аргумента функции.

y=f(x)-f(x0)=f(x0+x)-f(x0) – приращение функции, вызванное приращением аргумента.

Определение: функция y=f(x) называется непрерывной в точке х0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Непрерывность функции в интервале и на отрезке

функция y=f(x) называется непрерывной в интервале от a до b (a;b), если она непрерывна в каждой точке этого интервала.

Функция y=f(x) называется непрерывной на отрезке [a;b], если она непрерывна в каждой точке интервала (a;b) и в точке х=а непрерывна справа, а в точке х=b непрерывна слева.

12 Классификация точек разрыва

Если в точке х0 условие непрерывности нарушается, то говорят, что функция в точке х0 терпит разрыв/имеет точку разрыва.

Условие непрерывности: предел справа существует и конечен, предел слева существует и конечен, они равны между собой и равны значению функции в точке.

Точка х0 называется точкой разрыва первого рода, если в этой точке существуют конечные пределы функции справа и слева, но не равны значению функции; если эти пределы равны, то разрыв называется устранимым.

Точка х0 называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует или бесконечен.

19. Геометрический смысл производной

прямая y-y0=k(x-x0), угловой коэффициент которой равен производной функции в данной точке (k=f’(x0)) называется касательной к графику функции в данной точке.

При х0, значение х0+хх0, т.е. секущая стремиться занять положение касательной, так будем говорить, что касательная есть предельное положение секущей.

Геометрический смысл производной состоит в том, что она равна tg угла наклона касательной.

Прямая, перпендикулярная касательной в точке касания называется нормалью. -уравнение нормали в точке х0