12) Однородные системы

Однородной системой линейных уравнений называется система вида:

Нулевое решение системы (1) называется тривиальным решением.

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.

Решения однородной системы обладают свойством линейности:

Теорема (о линейном решении однородных систем).

Пусть — решения однородной системы (1), — произвольные константы. Тогда также является решением рассматриваемой системы

15)Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Необходимость

Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец b является линейной комбинацией столбцов матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что

Достаточность

Пусть . Возьмем в матрице A какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A. .

13) Теорема о ранге.

 

Определение 4.3. Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы.

 

Определение 4.4. Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).

В противном случае строки (столбцы) называются линейно независимыми.

 

Замечание. Можно доказать, что необходимым и достаточным условием линейной зависимости строк матрицы является то, что одна из них является линейной комбинацией остальных.

Теорема 4.1. Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией этих строк (столбцов).

 

Доказательство (для строк).

1. Если бы базисные строки были линейно зависимыми, то с помощью эквивалентных преобразований из них можно было бы получить нулевую строку, что противоречит условию, что базисный минор не равен 0.

2. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0.

Докажем это свойство для строки, не входящей в базисный минор.

Добавим к базисному минору эту строку (пусть ее номер – k) и любой столбец матрицы (пусть его номер – j). Затем разложим полученный определитель, равный 0 (так как его порядок больше ранга матрицы) по j-му столбцу:

Поскольку является базисным минором, поэтому, разделив полученное равенство на , найдем, что

для всех j=1,2,…,n, где . Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана.

 

Совместность линейных систем.

 

Определение 4.5. Линейная система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

 

Определение 4.6. Совместная линейная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

 

Назовем расширенной матрицей системы (2.2) матрицу вида

, а матрицей системы – матрицу из коэффициентов при неизвестных.

 

Теорема 4.2 (теорема Кронекера-Капелли). Система (2.2) совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы.

 

Доказательство.

1)       Необходимость: пусть система (2.2) совместна и ее решение. Тогда

, (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть

2)       Достаточность: если то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации 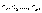то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.

 

Общее решение однородной линейной системы.

 

Рассмотрим однородную линейную систему

. (4.2)

Отметим, что такая система всегда совместна, поскольку имеет нулевое решение называемое тривиальным.

Пусть ранг матрицы системы r<n. Предположим, что в базисный минор входят коэффициенты первых r уравнений. Тогда оставшиеся m – r уравнений являются линейными комбинациями, то есть следствиями предыдущих. Поэтому можно оставить в системе только первые r уравнений:

.

Оставим в левой части каждого уравнения неизвестные, коэффициенты при которых входят в базисный минор, а остальные неизвестные перенесем направо:

(4.3)

Эта система будет иметь единственное решение относительно неизвестных 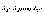выражающее их через остальные неизвестные ( ), которым можно придавать любые произвольные значения. Таким образом, система (4.2) при r<n является неопределенной.

 

Определение 4.7. Неизвестные коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные ( ) – свободными неизвестными.

 

Определение 4.8. Решения системы (4.2) (4.4) называются линейно независимыми, если линейная комбинация дает нулевой столбец только при

Покажем, что число линейно независимых решений системы (4.2) равно n – r. Действительно, рассмотрим столбцы вида

(4.5) содержащие по n-r чисел. Очевидно, что эти столбцы линейно независимы, а любой другой столбец той же размерности является их линейной комбинацией. Пусть эти столбцы задают значения свободных неизвестных системы (4.2).

Тогда базисные неизвестные будут однозначно определяться для выбранных свободных неизвестных из системы (4.3) по правилу Крамера, и все решения системы, соответствующие наборам свободных неизвестных (4.5), образуют n-r линейно независимых столбцов вида (4.4), то есть n-r линейно независимых решений системы (4.2).

 

Определение 4.9. Любые n – r линейно независимых решений системы (4.2) называются ее фундаментальной системой решений.

 

Определение 4.10. Фундаментальная система решений линейной однородной системы, в которой свободные неизвестные задаются по формулам (4.5), называется нормальной фундаментальной системой решений.

 

Замечание. Очевидным образом доказываются свойства решений однородной линейной системы (4.2):

Свойство 1. Сумма решений системы (4.2) является ее решением.

Свойство 2. Столбец решений (4.2), умноженный на любое число, тоже есть решение этой системы.

 

Следовательно, любая линейная комбинация фундаментальной системы решений системы (4.2) является ее решением. Можно доказать и обратное утверждение:

 

Теорема 4.3(без доказательства). Любое решение однородной линейной системы (4.2) является линейной комбинацией фундаментальной системы ее решений.

 

Таким образом, любое решение системы (4.2) имеет вид:

, где - фундаментальная система решений.

 

Пример.

Решим систему . Найдем ранг матрицы системы 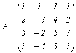. Преобразуем ее к виду: . Очевидно, что r(A)=2.

Пусть 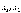- базисные неизвестные, - свободные неизвестные. Заменим исходную систему системой из первых двух уравнений, коэффициенты которых входят в базисный минор, и перенесем базисные неизвестные в правые части уравнений:

. Пусть . Тогда Если

то Получена фундаментальная система решений: .

Теперь общее решение системы можно записать в виде: , где С₁ и С₂ – любые произвольные числа.

 

Структура общего решения неоднородной линейной системы.

 

Рассмотрим неоднородную линейную систему (2.2):

.

Докажем следующие свойства ее решений:

Свойство 1. Сумма любого решения системы (2.2) и любого решения соответствующей однородной системы (4.2) является решением системы (2.2).

 

Доказательство.

Пусть с₁, с₂,…,с_n – решение системы (2.2), а d₁, d₂,…,d_n – решение системы (4.2) с теми же коэффициентами при неизвестных. Подставим в систему (2.2) x_i=c_i+d_i:

.

После перегруппировки слагаемых получим:

.

Но Следовательно, x_i=c_i+d_i является решением системы (2.2).

 

Свойство 2. Разность любых двух решений неоднородной системы (2.2) является решением соответствующей однородной системы (4.2).

 

Доказательство.

Пусть и - решения системы (2.2). Тогда

Утверждение доказано.

 

Следствие. Общее решение неоднородной системы (2.2) представляет собой сумму общего решения соответствующей однородной системы (4.2) и частного решения системы (2.2).

 

Пример.

Общее решение системы можно записать в виде:

, где - частное решение данной системы.

это множество элементов, называемых векторами, над которыми определённым образом определены операции сложения и умножения на число. В любом линейном пространстве можно выделить особую систему векторов, называемых 00007081%22базисом"базисом линейного пространства. Количество векторов в базисе равно размерности пространства. Любой вектор из пространства можно представить, как линейную комбинацию базисных векторов

Правило треугольника. Для сложения двух векторов и по правилу 0210510300180080треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Правило параллелограмма. Для сложения двух векторов и по правилу 09001000005000310000параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

А модуль (длину) вектора суммы 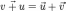определяют по 0205010500000108011002теореме косинусов где  — угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула теперь  — угол между векторами выходящими из одной точки.

Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.

Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.

Сложение коллинеарных скользящих векторов

Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В 02050105108105100018005100008000механике при изучении 01100108000статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы и , расположенные на одной прямой. Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы

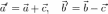
Прямые, на которых расположены векторы и , пересекаются всегда, за исключением случая, когда векторы и равны по величине и противоположны по направлению, в котором говорят, что векторы и образуют пару (векторов).

Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.

Законы умножения вектора на число.

     I.      1 · a = a ,  0 · a = 0 ,  m · 0 = 0 ,  ( –1 ) · a = – a .

     II.     m a = a m ,  | m a | = | m | · | a | .

     III.    m ( n a ) = ( m n ) a .          ( С о ч е т а т е л ь н ы й   

                                                              закон умножения на число ).

     IV.    ( m + n ) a = m a +  n a ,   ( Р а с п р е д е л и т е л ь н ы й

            m ( a + b ) = m a + m b .     закон умножения на число ).

Скалярное произведение векторов.   __     __

Угол между ненулевыми векторами  AB и CD – это угол, образованный векторами при их параллельном переносе до совмещения точек A и C. Скалярным произведением векторов a и b называется число, равное произведению их длин на косинус угла между ними:

 

Если один из векторов нулевой, то их скалярное произведение в соответствии с определением равно нулю: 

( a , 0 ) = ( 0 , b ) = 0 .

Если оба вектора ненулевые, то косинус угла между ними вычисляется по формуле:

Скалярное произведение ( a , a ), равное | a | 2, называется скалярным квадратом. Длина вектора  a  и его скалярный квадрат связаны соотношением: 

 

Скалярное произведение двух векторов:

   -  положительно, если угол между векторами острый ;

   -  отрицательно, если угол между векторами тупой .

Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда угол между ними прямой, т.е. когда эти векторы перпендикулярны (ортогональны):

 

 

Свойства скалярного произведения. Для любых векторов  a , b , c и любого числа m справедливы следующие соотношения:

I.   ( a , b ) = ( b , a ) .          ( П е р е м е с т и т е л ь н ы й   закон )

II.  ( m a , b ) = m ( a , b ) .

III. ( a + b , c ) = ( a , c ) + ( b , c ).  ( Р а с п р е д е л и т е л ь н ы й   закон

Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.