5) Матрицы их виды и операции над ними
ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО (каждый элемент матрицы умножить на число)
Умножение, МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, МОЖНО УМНОЖИТЬ НА МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА И ТОЛЬКО ТОГДА, КОГДА ЧИСЛО СТОЛБЦОВ МАТРИЦЫ A РАВНО ЧИСЛУ СТРОК МАТРИЦЫ B
КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦ
6)Транспонирование матриц
Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.
Пример 1. Составить транспонированную матрицу, полученную из А:
Решение: Поменяем местами строки и столбцы, сохраняя порядок:
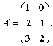
6)
Матрица
В называется обратной матрицей для
квадратной матрицы А , если
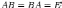
где Е — единичная матрица n-го порядка. Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная
матрица для матрицы А обозначается
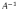
Найдите
обратную матрицу для матрицы
Решение.
Находим определитель
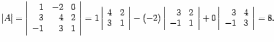
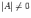то
матрица -- невырожденная, и обратная
для нее существует. Находим алгебраические
дополнения:
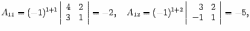
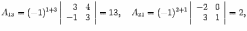
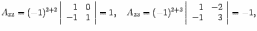
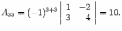
оставляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй -- строке:
(
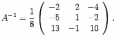14 .15) Полученная матрица и служит ответом
к задаче.
7) Матричные уравнения
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например,
чтобы найти матрицу Х из уравнения
необходимо умножить это уравнение на
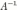слева.
Тогда:
Решить уравнение АХ = В, если
9) Линейная зависимость
Если какой-либо вектор можно представить в виде линейной комбинации, то говорят о линейной зависимости данного вектора от элементов комбинации.
Точнее, говорят так: некоторая совокупность элементов векторного пространства называется линейно зависимой, если существует равная нулю линейная комбинация элементов данной совокупности или
где не все числа равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.
Линейная зависимость векторов означает, что какой-то вектор заданной совокупности линейно выражается через остальные векторы.
Каждая матрица представляет собой совокупность векторов (одного и того же пространства). Две такие матрицы — две совокупности. Если каждый вектор одной совокупности линейно выражается через векторы другой совокупности, то на языке теории матриц этот факт описывается при помощи произведения матриц:
если строки матрицы C линейно зависят от строк матрицы B, то C = AB для некоторой матрицы A;
если столбцы матрицы C линейно зависят от столбцов другой матрицы A, то C = AB для некоторой матрицы B.
[править]
Ранг матрицы
Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы.
Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матриц\