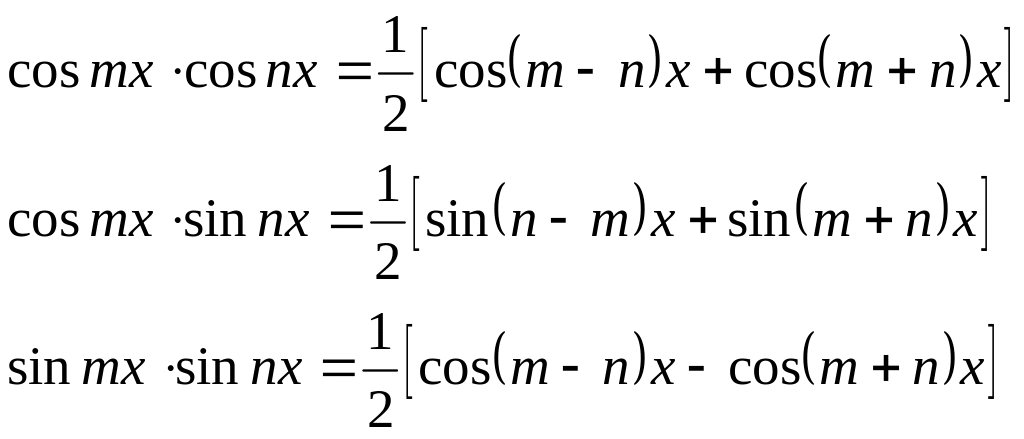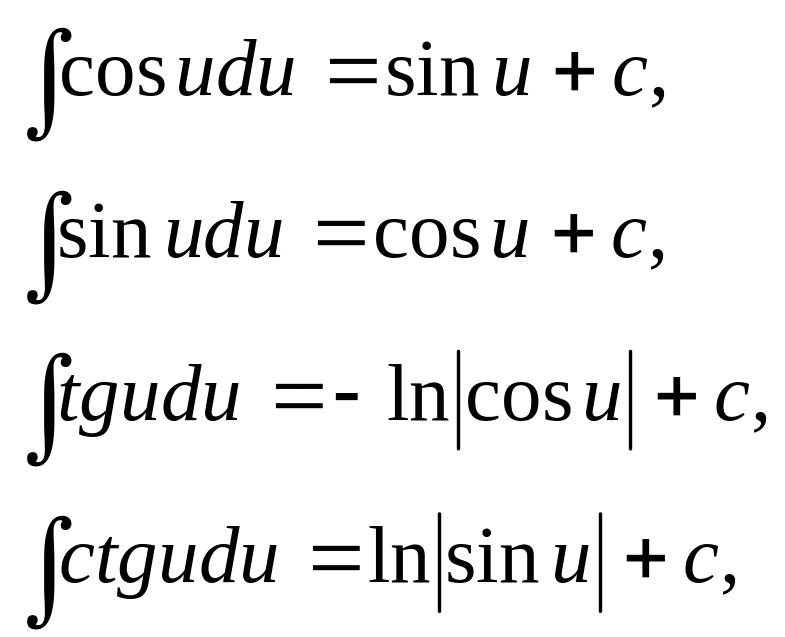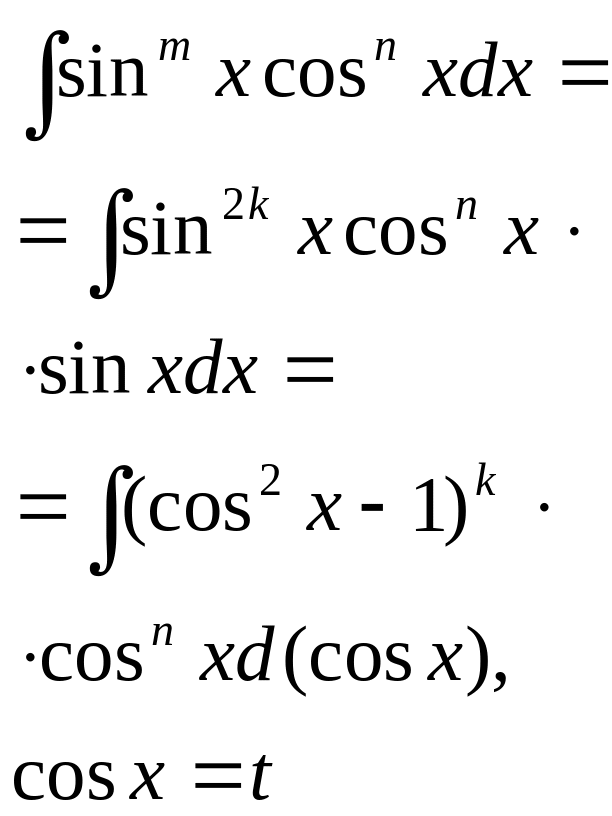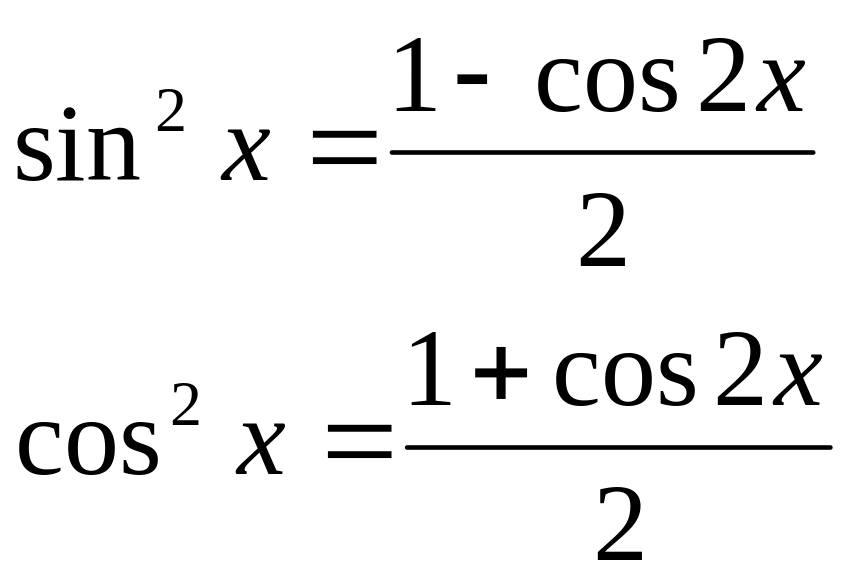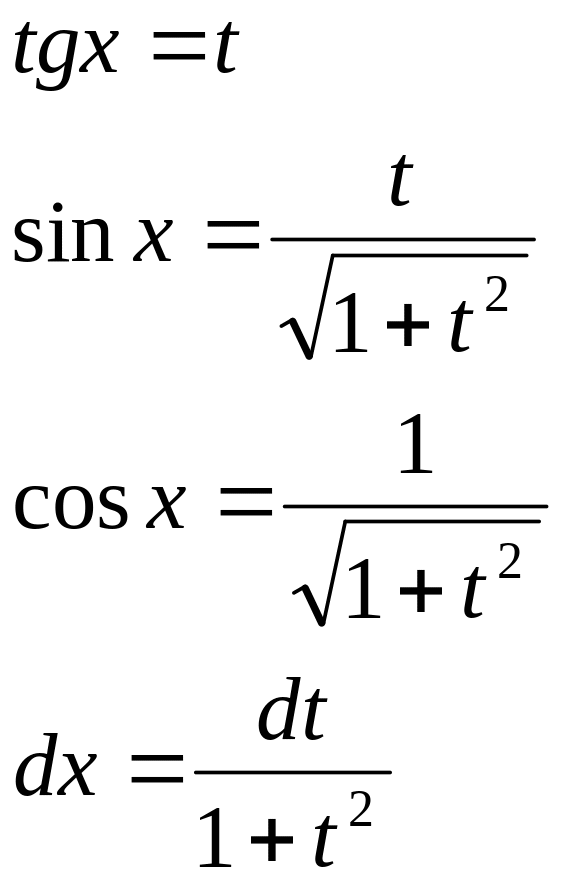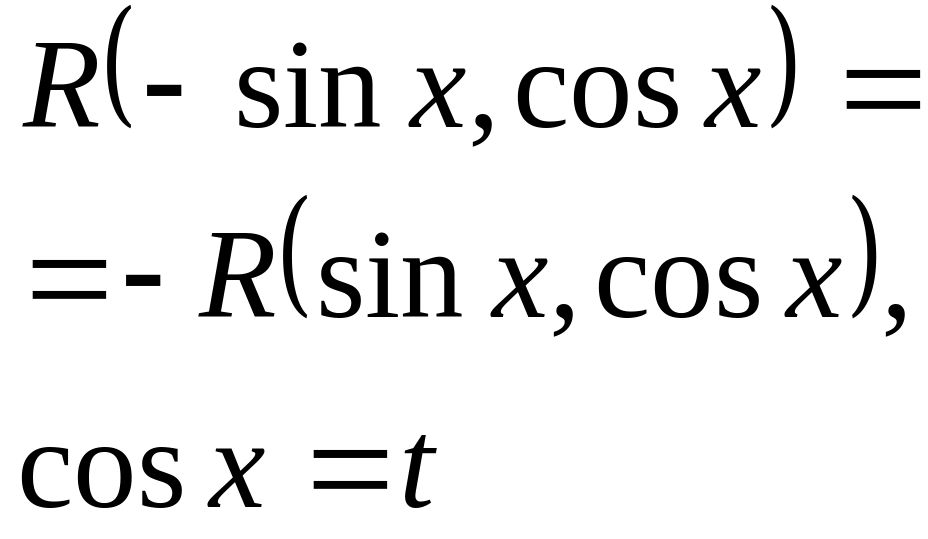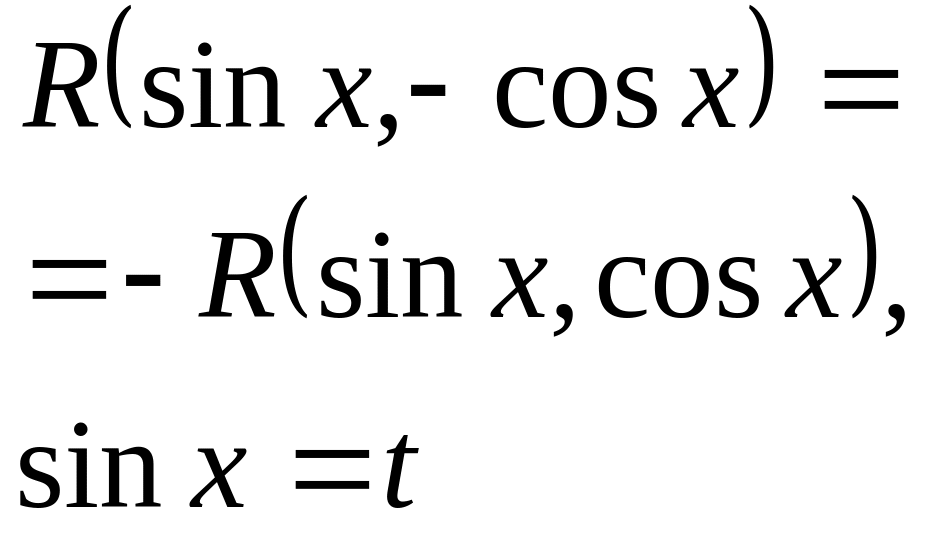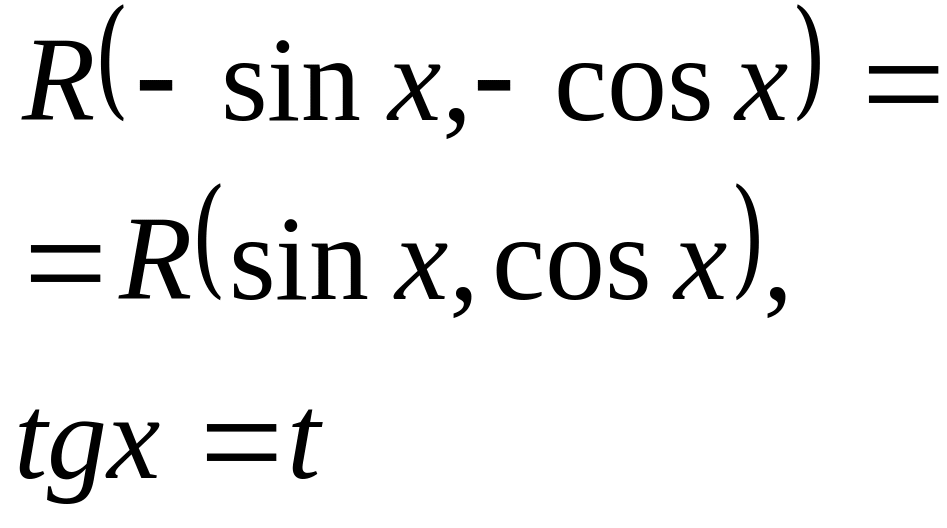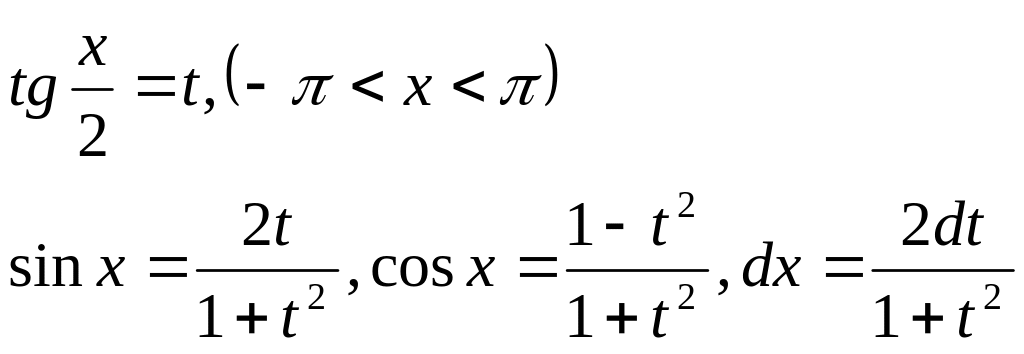П.2 Свойства неопределенных интегралов
Теорема
1.
.
Доказательство:
.
■
Теорема
2.
.
Доказательство:
.
■
Теорема
3.
(с точностью
до константы).
Доказательство:
.
■
Теорема
4.
Доказательство:
Для доказательства возьмем производную от обеих частей равенства. ■
П.3 Таблица основных интегралов
Пусть
,
где
- не обязательно независимая переменная.
Тогда, продифференцировав правую и
левую части нижеследующих равенств,
легко убедимся в их справедливости.
Данная таблица не исчерпывающая, а
наоборот - легко пополнимая.
При пользовании таблицей следует учитывать комментарий п.1.
1.
;
2.
;
3.
;
4.
;
5.
;
6.
;
7.
;
8.
;
9.
;
10.
;
11.
;
12.
;
13.
;
14.
;
15.
;
16.
.
Замечание. Следует отметить, что если операция дифференцирования замкнута на классе элементарных функций, то операция интегрирования элементарных функций таковой не является, так как неопределенный интеграл от некоторых элементарных функций не являются элементарной функцией.
Пример.
- интеграл Пуассона,
- интегралы Френеля,
- интегральные логарифм, синус и косинус,
соответственно. Эти функции в силу их
важности протабулированы.
П. 4 Общие методы интегрирования
Прямое применение формул.
Пример.
.
Разложение подынтегральной функции.
Пример.
.
3. Замена переменных.
а) неявная замена (внесение под знак дифференциала).
Пример.
,
;
б) явная замена.
Первый
вариант :
.
Тогда
и
.
Пример.
.
Второй
вариант : какая-та часть подынтегральной
функции заменяется на
или на
.
Пример.
.
Замечание. Обратим внимание, что форма ответов не совпадает, т.е. форма ответа зависит от метода интегрирования. Покажем, что отличаются ответы только по форме.
Так
как
,
то
,
т. е.
.
Таким образом, надо показать, что
.
Пусть
,
т.е.
.
Возьмем тангенс от обеих частей
доказываемого равенства
,
но
,
,
,
т.е.
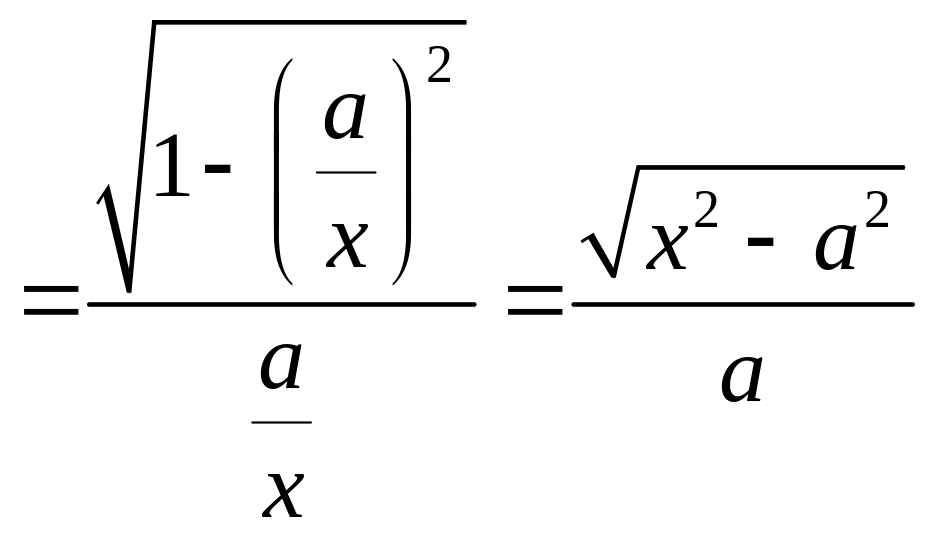и
.
■
4. Интегрирование по частям.
Теорема
1. Пусть
,
- функции, дифференцируемые
,
а функция
- интегрируемая
.
Тогда интегрируема функция
,
причем
имеет место равенство
.
Доказательство:
Рассмотрим
производную произведения функций
и
:
.
Тогда
.
Проинтегрируем обе части последнего
равенства:
.
Так как
,
,
,
то
.
Таким образом,
.
Обычно в подынтегральном выражении функцию, которую дифференцируют, принимают за , а ту, которую интегрируют, принимают за . Интегрирование по частям применяется чаще всего в следующих случаях.
I случай.
I-й тип |
II-й тип |
III-й тип |
|
|
|
,
где
За
принимаются подчеркнутые функции, а за
- остальная часть подынтегрального
выражения.
- это многочлен степени
.
Интегралы I-го
типа берутся
раз по частям, II-го
типа -
раз, III-го
типа (за исключением двух последних) -
2 раза, причем оба раза за
принимаем степенную функцию
или тригонометрические функции
,
в первом интеграле III-го
типа. По частям могут быть взяты и
интегралы, не принадлежащие к основным
типам интегралов.
Пример.
.
Пример.
Найдем
интеграл, приводящийся к себе:
.
Пример.
Найдем
интеграл, не принадлежащий к основным
типам интегралов
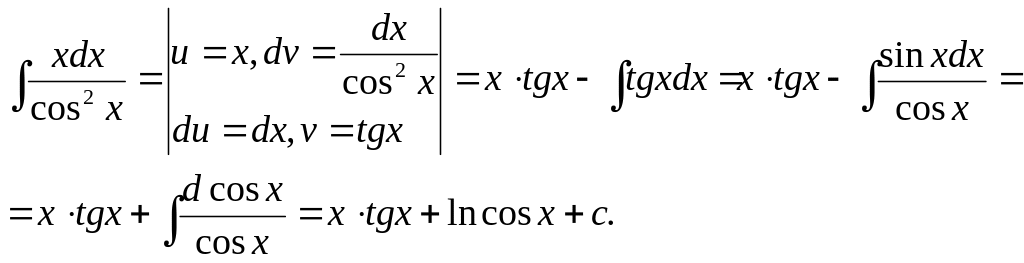
II случай. Рекуррентные формулы.
.
Таким
образом,
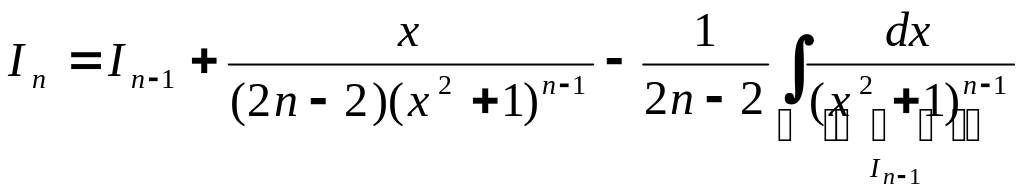или
.
5. Интегрирование рациональных дробей.
Как было показано раньше ( Гл. , п. ) существует 4 типа элементарных дробей. Интегрируются они стандартным образом.
I.
.
II.
.
III.
.
,
.
.
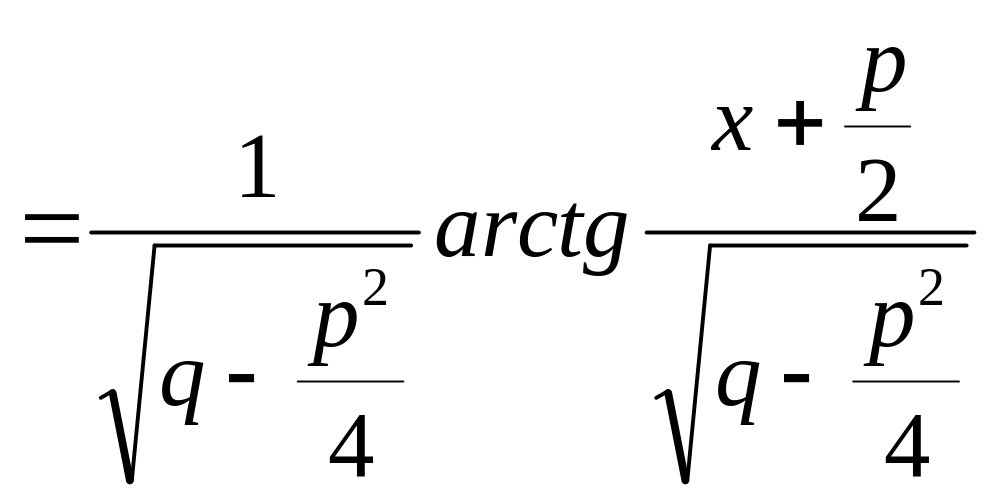Таким образом,
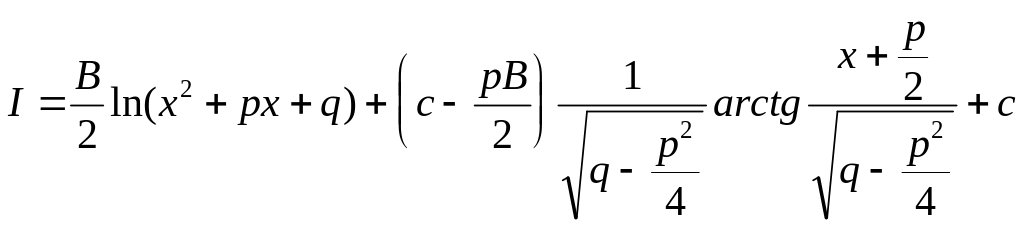
IV.
,
,
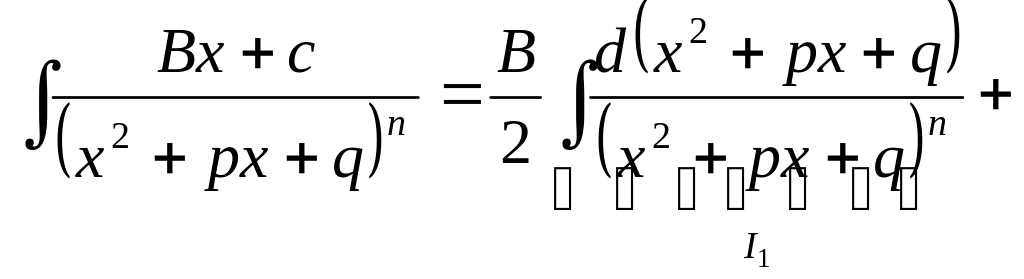
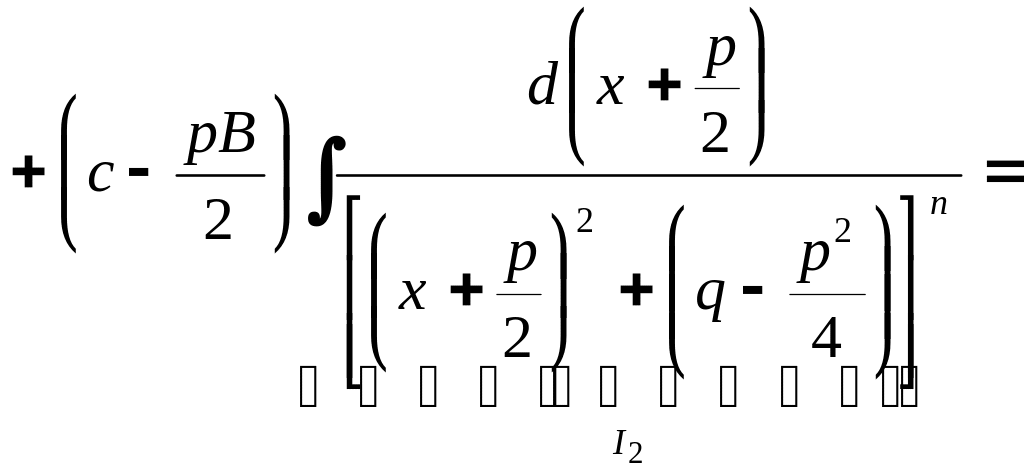
был
построен в п. 4.
6. Интегрирование тригонометрических функций.
Алгоритмы вычисления таких интегралов даются в прилагаемых ниже таблицах.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий случай:
|
7. Интегрирование иррациональных функций.
Алгоритмы вычисления таких интегралов даются в прилагаемых ниже таблицах.