2.7. Цепь переменного тока с параллельным соединением активного, индуктивного и ёмкостного сопротивлений.

При параллельном соединении активного, индуктивного и емкостного сопротивлений все ветви оказываются включенными под одним и тем же напряжением (рис. 2.15).

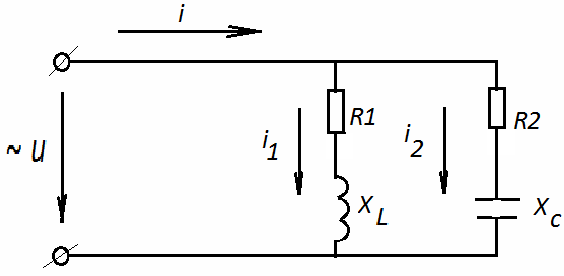
Рис. 2.15 Схема переменного тока с параллельным

соединением R, X_L, X_C.

Под действием подведённого напряжения в неразветвленной части цепи возникает ток i , который разветвляется по двум параллельным ветвям обратно пропорционально их сопротивлениям.

Составим по первому закону Кирхгофа уравнение мгновенных значений токов

В действующих значениях токов уравнение принимает вид:

Ток первой ветви , соответственно равны:

Ток второй ветви соответственно равны:

Ток в неразветвленной части цепи можно определить графически, путем построения векторной диаграммы. При параллельном соединении R,X_L, X_C в качестве базисного вектора выбирается вектор напряжения, т.к. он одинаков для всех ветвей схемы. Относительно этого вектора откладываются вектора токов (рис. 2.16).

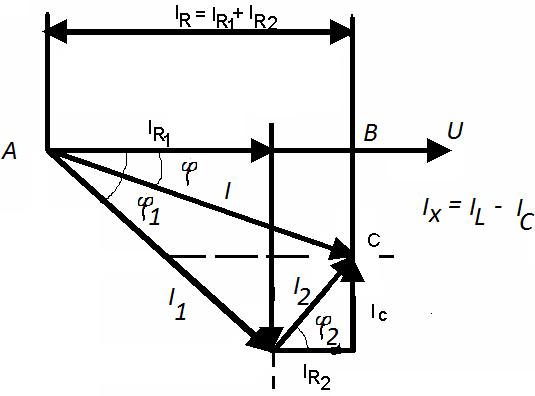
Рис. 2.16 Векторная диаграмма цепи переменного тока с параллельным соединением R, X_L, X_C.

Составляющие токов в ветвях определяются как

Активная составляющая общего тока в цепи равна арифметической сумме активных составляющих токов ветвей:

Реактивные составляющие токов в ветвях определяются как

Реактивная составляющая общего тока в цепи равна алгебраической сумме реактивных составляющих токов в ветвях:

В результате получается треугольник токов АВС (рис. 2.16), из которого получим:

(1)

В общем виде, в параллельных цепях переменного тока величина тока в неразветвленной части цепи определяется по формуле:

Кроме того, из треугольника токов можно получить следующие соотношения:

Активная мощность цепи с параллельным соединением определяется как арифметическая сумма активных мощностей ветвей:

Реактивная мощность цепи определяется как алгебраическая сумма реактивных мощностей ветвей:

Единица измерения реактивной мощности является вольт ампер реактивный [ВАр]

2.8. Понятие эквивалентной проводимости.

В цепях переменного тока с параллельным соединением активного, индуктивного и емкостного сопротивлений группу параллельно соединенных электроприёмников можно заменить их эквивалентным сопротивлением, так же, как и в цепях постоянного тока. Значения сопротивлений R_эк и X_эк удобнее находить, если ввести понятие эквивалентной проводимости. Рассмотрим слагаемые в правой части (1):

, (2)

где – активная проводимость первой ветви

, (3)

где – активная проводимость второй ветви.

, (4)

где – индуктивная проводимость первой ветви

, (5)

где – емкостная проводимость второй ветви.

Где – полная эквивалентная проводимость цепи.

Между полной проводимостью и полным сопротивлением существует обратно пропорциональная зависимость:

Зная можно определить эквивалентные активное и реактивное сопротивления