1.8. Метод контурных токов.

Метод контурных токов дает возможность упростить расчет электрических цепей за счет уменьшения числа решаемых уравнений.

Сущность метода поясним на примере сложной цепи, схема которой представлена на рис. 1.11. Эту сложную цепь разбиваем на три смежных контура с произвольно выбранным направлением токов. Будем считать, что в каждом из этих контуров проходит свой контурный ток I_I , I_II , I_III ,тогда токи в смежных ветвях будут равны алгебраической сумме контурных токов.

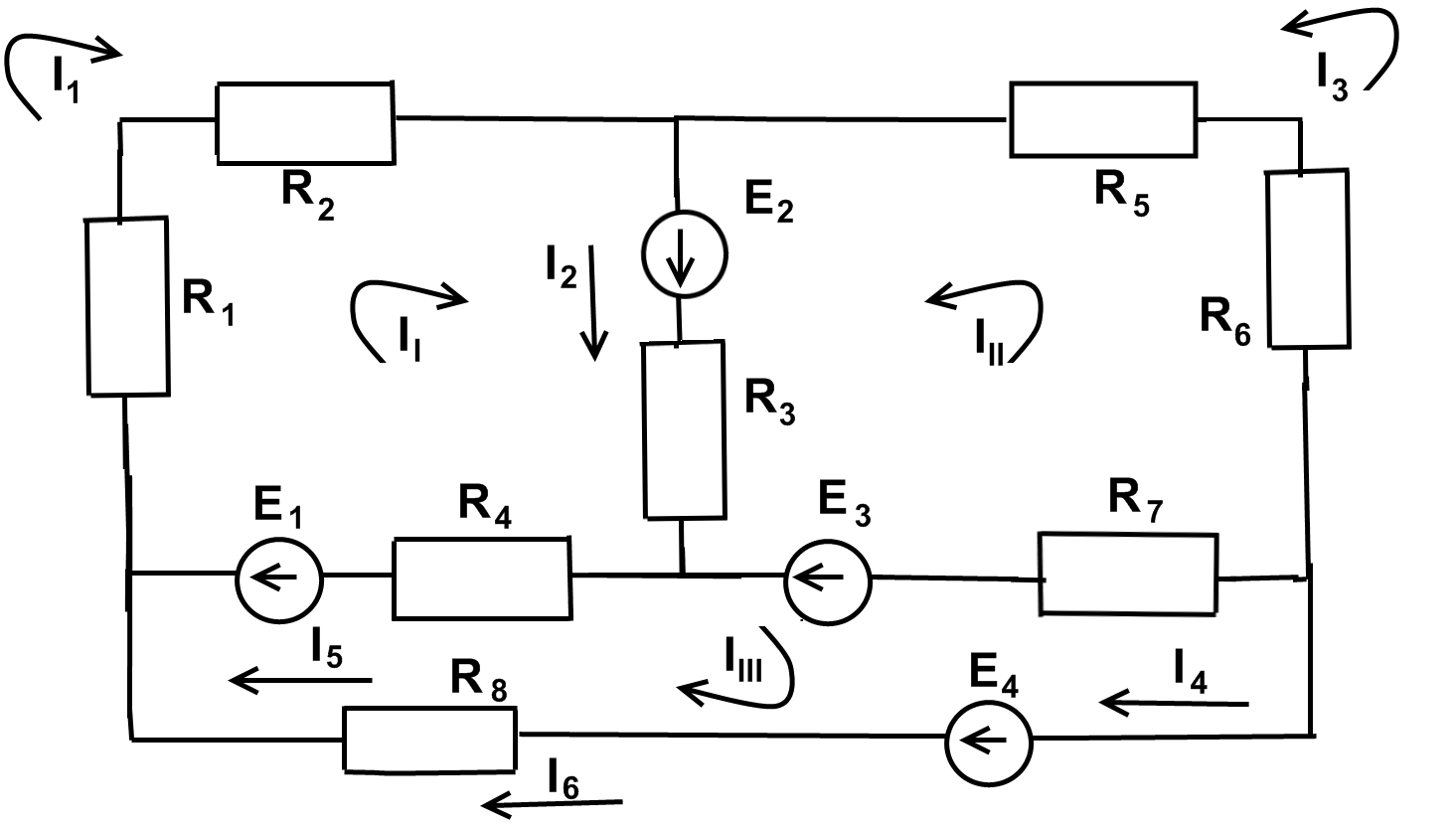
Рис. 1. 11.

Применяя к контурам второй закон Кирхгофа, составим систему уравнений

E₁ +E₂= I_I (R₁ + R₂) + (I_I – I_II) R₃ + (I_I – I_III) R₄

E₃ - E₂= I_II (R₅ + R₆) + (I_II – II_III) R₇ + (I_II – I_I) R₃

E₄ – E₁- E₃= I_IIIR₈ + (I_III – I_I) R₄ + (I_III – I_II) R₇

После несложных преобразований система уравнений примет вид:

E₁ + E₂ = I_I (R₁ + R₂ + R₃ +R₄) – I_IIR₃ – I_IIIR₄

E₃ - E₂ = I_II (R₅ + R₆ + R₇ +R₃) – I_IR₃ – I_IIIR₇

E₄ – E₁ – E₃ = I_III (R₈ + R₄ + R₇) – I_IR₄ – I_IIR₇

Из этой системы уравнений определяют значения контурных токов I_I, I_II, I_III. Токи в смежных ветвях определяют как алгебраическую сумму контурных токов.

В рассматриваемой цепи шесть ветвей, значит, необходимо найти шесть токов.

I₁=I_I

I₂=I_I-I_II

I₃=I_II

I₄=I_II-I_III

I₅=I_I-I_III

I₆=I_III

Проверку решения задачи осуществляют путем составления уравнения баланса мощностей с реальными токами.

2. Однофазный переменный ток

2.1. Получение однофазного переменного тока.

Основными преимуществами переменного тока перед постоянным являются:

1. Относительная простота конструкции и надежность в эксплуатации генераторов переменного тока;

2. Возможность передачи переменного тока практически на любые расстояния с помощью современных трансформаторов;

3. Двигатели переменного тока проще, надёжнее и дешевле двигателей постоянного тока.

Рис. 2.1 Генератор переменного тока.

Получение однофазного переменного тока можно пояснить из следующей схемы (рис. 2.1). Между полюсами N и S постоянного магнита помещён виток провода, начало и конец которого присоединены к двум изолированным друг от друга кольцам К₁ и К₂. На кольца наложены токосъемные щетки С₁ и С₂ к которым через ключ К подключается нагрузка R.

Если привести виток во вращение, то магнитные силовые линии начнут пронизывать проводники витка ab и cd и, в соответствии с законом электромагнитной индукции, в них будет наводиться ЭДС индукции, определяемая законом Фарадея:

(1)

где – мгновенное значение ЭДС (B);

B – магнитная индукция измеряемая в теслах (Тл);

– длина проводника ab или cd (м);

V – скорость вращения витка (м/сек);

– угол между вектором магнитной индукции и направлением движения проводника в магнитном поле.

При одном полном обороте витка угол принимает все значения от 9 до 360° и, как следствие этого, ЭДС проходит полный цикл изменения по синусоидальному закону. При , ЭДС достигает своего максимального значения Em:

(2)

Подставляя (2) в (1) имеем:

(3)

Если вращение витка будет происходить с постоянной угловой скоростью ω, то угол =ωt (4).

Подставляя (4) в (3), получим:

При замыкании ключа К (рис. 2.1) по замкнутой цепи потечет электрический ток, мгновенное значение которого , согласно закону Ленца, будет изменяться во времени так же как и ЭДС по синусоидальному закону:

Этот ток, проходящий по сопротивлению нагрузки R, вызывает на его зажимах синусоидальное падение напряжения, мгновенное значение которого равно:

В цепях переменного тока различают мгновенные, амплитудные и действующие значения ЭДС, тока и напряжения. Значение переменной величины в произвольный момент времени называют мгновенным значением. Мгновенные значения ЭДС, тока и напряжения обозначаются соответственно через , и . Наибольшее значение этих величин называют амплитудным или максимальным значением. Амплитудные значения ЭДС, тока и напряжения обозначаются соответственно через .

Действующее значение ЭДС, тока и напряжения обозначаются соответственно через и определяются по формулам :

; ; ;

На рис. 2.2 приведена волновая диаграмма тока

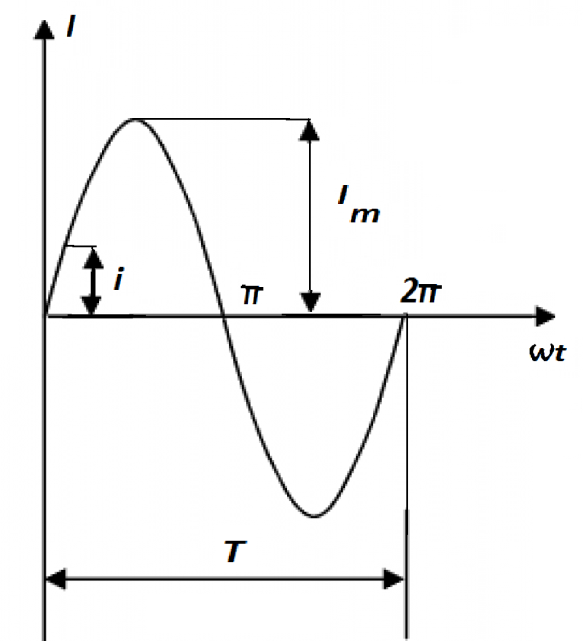
Рис. 2.2 Волновая диаграмма однофазного переменного тока.

Волновые диаграммы ЭДС и напряжения имеют аналогичный вид.

Промежуток времени, в течении которого проходит полный цикл изменения синусоидальной величины, называется периодом и обозначается буквой Т (рис. 2.2).

Число периодов в единицу времени называется частотой и обозначается буквой ƒ и измеряется в герцах.

Между угловой частотой ω, измеряемой в радианах в секунду, и частотой электрического тока ƒ существует прямая пропорциональная зависимость: