
- •1.Понятие случайного события, виды случайных событий.
- •2.Классическое и статистическое определение вероятности.
- •3.Теоремы сложения вероятностей для совместных и несовместных событий.
- •7.Испытания по схеме Бернулли,условияиспользования формулы Бернулли.
- •8.Локальная теорема Лапласа и условия ее применения.
- •9.Интегральная теорема Лапласа.
- •17.Нормальный закон распределения.
7.Испытания по схеме Бернулли,условияиспользования формулы Бернулли.
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание (опыт) испытания повторяется многократно.Под испытанием понимается осуществление определенного комплекса условий,в результате которых может произойти(или нет)то или иное событие пространства элементарных событий.
Повторные независимые испытания-многократные испытания,в которых вероятность поЯвления события А в каждом испытании не меняется в зависимости от исходов других испытаний.
Впервые схема независимых испытаний была рассмотрена Бернулли для важнейшего частного случая к=2.
Под схемой Бернулли понимают проведение серии в n испытаний,в каждом из которых возможны 2 исхода:либо наступит событие А,либо не наступит,т.е. произойдет противоположное ему,и при этом:
1.все n испытаний независимы.
2.вероятность события А в каждом отдельном испытании постоянна и не меняется от испытания к испытанию.
Р(А)=р;Р(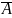 )=1-p=q.
)=1-p=q.
В случае небольшогочисла испытаний n вероятность Рn(m) того,что в n независимых испытаниях событие А наступит ровно m раз,определяется в соответствии с формулой Бернулли:
Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:
![]()
где Cnk — число сочетаний, q = 1 – p-вероятность противоположного события ( )
n-число испытаний Бернулли.
m-число испытаний ,в которых наступило событие А.
р=Р(А)-вероятность наступления события А в каждом испытании.
8.Локальная теорема Лапласа и условия ее применения.
При вычислении вероятностей в условиях большого числа испытаний можно столкнуться со значительными вычислительными трудностями.В связи с этим возникла необходимость в построении асимптотических(приближенных) формул,позволяющих с достаточной степенью точности определить Рn(m).Одними из них являются теоремы Муавра-Лапласа.
Локальная теорема Муавра — Лапласа. При большом числе испытаний n стремится к бесконечности, вероятности наступления события А в каждом испытанииа p, отличной от 0 и 1,и при выполнении условия npq>= 20 ,вероятность Pn(m) того,что в n независимых испытаниях событие А наступит ровно m раз,определяется в соответствии с локальной теоремой Лапласа:
![]()
Функция φ(x) называется функцией Гаусса.
q = 1 – p-вероятность противоположного события ( )
n-число испытаний Бернулли.
m-число испытаний ,в которых наступило событие А.
р=Р(А)-вероятность наступления события А в каждом испытании.
Функция гаусса представляет собой плотность стандартного нормального закона распределения .
Функция Гаусса:
1.f(t)-четная функция,т.е. f(t)=f(-t)
2.f(t)-монотонно убывающая функция,т.е. f(t) -> 0 при t -> +- бесконечности;при | t |> 5 можно считать f(t)≈0
9.Интегральная теорема Лапласа.
При
большом числе испытаний n стремится к
бесконечности, вероятности наступления
события А в каждом испытанииа p, отличной
от 0 и 1,и при выполнении условия npq>=
20 ,вероятность Pn(m)
того,что в n
независимых испытаниях событие А
наступит от a
и b
раз ,определяется соответствии с
интегральной теоремой Лапласа.

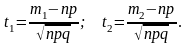
q = 1 – p-вероятность противоположного события ( )
n-число испытаний Бернулли.
m-число испытаний ,в которых наступило событие А.
р=Р(А)-вероятность наступления события А в каждом испытании.
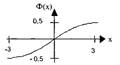
Функия Лапласа представляет собой функцию стандартного нормального распределения.
Ф(t) имеет следующие свойства:
1. Ф(-t)= -Ф(t) - функция нечетная, поэтому достаточно изучать её для неотрицательных значений х

2. Функция Ф(t) возрастает на всей числовой оси;
10.Формула Пуассона и условия ее применения.
При большом числе испытаний n стремится к бесконечности, вероятности наступления события А в каждом испытании p →0,и при выполнении условия 0,1≤np≤10,вероятность Pn(m) того,что в n независимых испытаниях событие А наступит ровно m раз,определяется в соответствии с теоремой Пуассона:
 ;
λ= np
;
λ= np
n-число испытаний Бернулли.
m-число испытаний ,в которых наступило событие А.
λ= np-параметр Пуассоновского распределения,называемый еще средней интенсивностью.Теорему можно доказать путем замены в формуле Бернулли вероятности р на λ\n и вычисления ее предела при n→∞.
Значения ф-ии Пуассона Pn(m) также могут быть определены по таблице для заданных значений m и λ.
Случайные события,к которым может быть применена теорема Пуассона,называют еще редкими событиями ввиду малой вероятности наступленич события А в каждом испытании.
11.Понятие случайной величины,виды случайных величин.
Случайная величина является одним из основных понятий теории вероятностей. Случайная величина-переменная,которая в результате испытания принимает одно из своих возможных значений,причем заранее не известно,какое именно,так как это зависит от случая.
Связь случайной величины и случайного события заключается в том,что принятие случайной величиной некоторого числового значения набора возможных(т.е. выполнение равенства Х=хi) есть случайное событие,характеризующееся вероятностью Р(Х=хi)=pi.
Примеры случайных величин:
Число очков ,выпавших на верхней грани игрального кубика.
Число студентов,пришедших на лекцию.
Расстояние от центра мишени до точки попадания при выстреле
Сумма выплат по очередному страховому случаю.
В зависимости от характера области возможных значений можно выделить два вида случайных величин: дискретные и непрерывные.
Будем обозначать случайные величины большими латинскими буквами X, Y, T, ... , а соответствующие значения, которые они принимают, малыми буквами x, y, t, ...
Случайная величина называется дискретной, если она принимает конечное или счетное число значений. Дискретная случайная величина задается с помощью ряда распределения - функции, ставящей в соответствие каждому возможному значению случайной величины определенную вероятность. Таким образом, ряд распределения - это конечное или счетное множество пар элементов.
Непрерывная случайная величина-случайная вличина,бесконечное и несчетное множество значений которой есть некоторый интервал(конечный или бесконечный),и она сплошь заполняет этот интервал.
Следовательно ,закон распределения непрерывной случайной величины нельзя задать рядом распределения.Для этого используются интегральная и дифференциальная функции распределения.
12. Плотность и функция распределения случайной величины.
Плотностью распределения вероятностей непрерывной случайной величины называют функцию — первую производную от функции распределения : F(x)
![]()
Из этого определения следует, что функция распределения является первообразной для плотности распределения.
П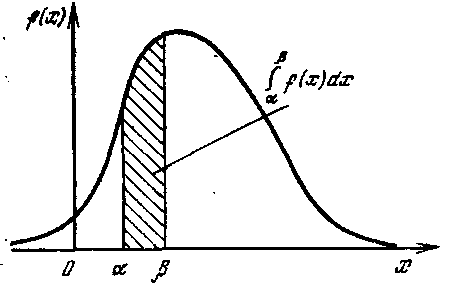 лотность
распределения случайной величины и ее
свойства. С
помощью плотности
распределения
можно задавать закон распределения
только непре-рывной случайной величины.
f(x)
= F’(x)
=
лотность
распределения случайной величины и ее
свойства. С
помощью плотности
распределения
можно задавать закон распределения
только непре-рывной случайной величины.
f(x)
= F’(x)
=
 ;
F(x)
=
;
F(x)
=
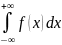 .
Свойства:
1)F(x)
≥ 0; 2) P(a<x<b)
=
.
Свойства:
1)F(x)
≥ 0; 2) P(a<x<b)
=
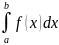 ,
=1.
,
=1.
Функция распределения случайной величины и ее свойства. Функцией распределения F(x) случайной величины X называется вероятность события, состоящего в том, что случайная величина X примет значение строго меньше аргумента этой функции, т.е. x. F(x)=P(X<x). С помощью функции распределения можно задавать закон распределения как дискретной, так и непре-рывной слу-чайной вели-чины. Для дискретной слу-чайной вели-чины ф-ция раз-рывная и ступенчатая, принимает значения от 1 до 0. Если случайная величина непрерывна, то функция распределения будет непрерывной неубывающей функцией, заключенной между 0 и 1. Свойства:
0 ≤ F(x) ≤ 1,
F(x+ )
≥ F(x)
)
≥ F(x)
F( )
= 1
)
= 1
F(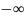 )
= 0
)
= 0
Если X непрерывна, то вероятность того, что она примет кон-кретные значения равна 0.
14.
Математическое ожидание случайной
величины и его свойства. Математическое
ожидание
характеризует положение случайной
величины на числовой оси, определяет
некоторое среднее значение, около
которого сосредоточены все возможные
значения этой случайной величины.
Математическое ожидание часто называют
средним значением случайной величины.
M[x]
– математическое ожидание x.
Если случайная величина дискретна,
т.е. задана в виде таблицы,
то
ее математич. ожидание: M[x]=
mx
=
x1p1
+
x2p2
+
… + xipi
+
… + xnpn
=
 .
Понятию математ. ожидания для дискретной
случайной величины можно придать
следующий физический
смысл:
Если
приложить грузик, то вес будет равен
вероятности.
Если
случайная величина непрерывна
и ее закон распределения задан в виде
плотности, то
M[x]
]= mx
=
.
Понятию математ. ожидания для дискретной
случайной величины можно придать
следующий физический
смысл:
Если
приложить грузик, то вес будет равен
вероятности.
Если
случайная величина непрерывна
и ее закон распределения задан в виде
плотности, то
M[x]
]= mx
=
 .
Физический
смысл:
координата по оси X
центра тяжести фигуры, ограниченной
сверху графиком распределения. Свойства:
1)
Мат.ож.
константы = const.
M[c]
= c.
2) Мат. ожидание суммы двух случайных
величин = сумме мат. ож. этих случайных
величин, т.е. M[x+y]
= M[x]
+ M[y],
M[
.
Физический
смысл:
координата по оси X
центра тяжести фигуры, ограниченной
сверху графиком распределения. Свойства:
1)
Мат.ож.
константы = const.
M[c]
= c.
2) Мат. ожидание суммы двух случайных
величин = сумме мат. ож. этих случайных
величин, т.е. M[x+y]
= M[x]
+ M[y],
M[ ] =
] =
 .
3) Если закон распределения случайной
величины x
никак не изменяется от того, какое
значение приняла величина y
(x
и y
независимы), то для таких случайных
величин справедлива формула: M[xy]
= M[x]M[y].
Следствие
1: M[cx]
= cM[x].
След.
2:
мат. ож. отклонения случайной величины
от ее мат. ож. равно 0: M[x-M[x]]
= 0. Случайная величина (x-M[x])
называется центрированной случайной
величиной и обозначается x0.
.
3) Если закон распределения случайной
величины x
никак не изменяется от того, какое
значение приняла величина y
(x
и y
независимы), то для таких случайных
величин справедлива формула: M[xy]
= M[x]M[y].
Следствие
1: M[cx]
= cM[x].
След.
2:
мат. ож. отклонения случайной величины
от ее мат. ож. равно 0: M[x-M[x]]
= 0. Случайная величина (x-M[x])
называется центрированной случайной
величиной и обозначается x0.
15.
Дисперсия и ее свойства,среднее
квадратичное отклонение. Эти
числовые характеристики показывают
насколько велико рассеивание случайной
величины относительно среднего значения
этой случайной величины. Dx
= D[x]
=
 = M[
= M[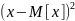 ]
равно: 1)
]
равно: 1)
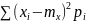 - для дискретных; 2)
- для дискретных; 2)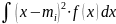 - для непрерывных. Важное:
1) Дисперсия всегда больше 0; 2.) Ее
размерность – квадрат размерности
случайной величины. Чтобы сделать так,
чтобы размерность случайной величины
x
и размерность числовой характеристики,
определя-ющей величину разброса случайной
величины относительно среднего значения,
совпадала, рассмо-трим корень квадратный
из дисперсии.
- для непрерывных. Важное:
1) Дисперсия всегда больше 0; 2.) Ее
размерность – квадрат размерности
случайной величины. Чтобы сделать так,
чтобы размерность случайной величины
x
и размерность числовой характеристики,
определя-ющей величину разброса случайной
величины относительно среднего значения,
совпадала, рассмо-трим корень квадратный
из дисперсии.
 =
=
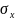 наз.
средним
квадратичным отклонением.
Свойства:
1) Дисперсии константы есть константа.
D[c]=0;
2) Постоянный множитель случайной
величины можно выносить за знак дисперсии,
предварительно возведя его в квадрат
D[cx]=c2D[x];
3) Если случайные величины независимы
D[x+y]
= D[x]+D[y];
D[x-y]
= D[x+(-1)y]
= D[x]
+ D[(-1)y]
= D[x]+D[y];
4) Дисперсия случайной величины равна
разности между мат. ож. квадрата случайной
величины и квадратом мат. ож. этой
случайной величины. D[x]
= M[x2]
– M2[x];
D[x] = M[(x-mx)2]
= M[x2-2mxx+mx2]
= M[x2]
– M[2mxx]
+ M[mx2]
= M[x2]
- 2mxM[x]
+ mx2=
M[x2]
- mx2
= M[x2]
– M2[x].
Свойство
4 позволяет упростить вычисление
дисперсии.
наз.
средним
квадратичным отклонением.
Свойства:
1) Дисперсии константы есть константа.
D[c]=0;
2) Постоянный множитель случайной
величины можно выносить за знак дисперсии,
предварительно возведя его в квадрат
D[cx]=c2D[x];
3) Если случайные величины независимы
D[x+y]
= D[x]+D[y];
D[x-y]
= D[x+(-1)y]
= D[x]
+ D[(-1)y]
= D[x]+D[y];
4) Дисперсия случайной величины равна
разности между мат. ож. квадрата случайной
величины и квадратом мат. ож. этой
случайной величины. D[x]
= M[x2]
– M2[x];
D[x] = M[(x-mx)2]
= M[x2-2mxx+mx2]
= M[x2]
– M[2mxx]
+ M[mx2]
= M[x2]
- 2mxM[x]
+ mx2=
M[x2]
- mx2
= M[x2]
– M2[x].
Свойство
4 позволяет упростить вычисление
дисперсии.
16.Понятие о законе распределения случайной величины,примеры законов распределения.
Закон распределения-соотношение,устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями,с которыми случайная величина принимает эти значения.
Примеры:биномиальный,пуассона,равномерный закон распределения.
Биномиальный
закон распределения и его свойства.
Производится
n
независимых опытов, в каждом из которых
может наступить или не наступить событие
A,
где вероятность наступления события
A:
P(A)
= p,
а вероятность того, что событие А не
наступит т.е. обратного события
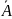 :
P(
:
P(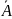 )
= 1 – p
= q;
Тогда вероятность
того что событие А, в n
независимых опытах, наступит ровно m
раз определяется формулой Бернулли:
)
= 1 – p
= q;
Тогда вероятность
того что событие А, в n
независимых опытах, наступит ровно m
раз определяется формулой Бернулли:
 ,
где
,
где
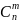 – число сочетаний из n
по m,
x
- случайная величина равная количеству
появлений события А. Так как формула
Бернулли является формулой для членов
разложения бинома
– число сочетаний из n
по m,
x
- случайная величина равная количеству
появлений события А. Так как формула
Бернулли является формулой для членов
разложения бинома
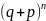 , то такое распределение вероятностей
называется биномиальным.
М.
ожидание:
, то такое распределение вероятностей
называется биномиальным.
М.
ожидание:
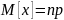 ;
Дисперсия:
;
Дисперсия:
 .
Биномиальное распре-деление применяется
для дискретных величин, однако при
большом количестве опытов приближается
к нормальному распределению (согласно
Центральной предельной теоремы).
.
Биномиальное распре-деление применяется
для дискретных величин, однако при
большом количестве опытов приближается
к нормальному распределению (согласно
Центральной предельной теоремы).
Закон
распределения Пуассона. Закон
распределения Пуассона
получается из биномиального закона
распределения, если число испытаний
“m”
неограниченно возрастает при одновременном
уменьшении вероятности наступления
“p”,
причем “np
= const”.
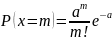 ,
где a
= np
= const
– параметр закона распределения
Пуассона.
Мат.
ожидание:
,
где a
= np
= const
– параметр закона распределения
Пуассона.
Мат.
ожидание:
 =
=
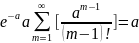 (тут получившаяся сумма сходится к
экспоненте в степени а и всё сокращается).
Дисперсия:
Т.к.
(тут получившаяся сумма сходится к
экспоненте в степени а и всё сокращается).
Дисперсия:
Т.к.
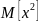 =
=
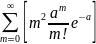 =
=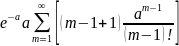 =
=
 ,
то D[x]
=
,
то D[x]
=
 =
=
 = a.
Равенство математического ожидания и
дисперсии является одной из особенностей
распределения Пуассона, эта особенность
часто применяется в математической
статистике. Распределением Пуассона
можно пользоваться, когда исследуемая
величина подчинена биномиальному закону
распределения, но при этом известно,
что “m”
– достаточно большое, а “p”
достаточная мала.
= a.
Равенство математического ожидания и
дисперсии является одной из особенностей
распределения Пуассона, эта особенность
часто применяется в математической
статистике. Распределением Пуассона
можно пользоваться, когда исследуемая
величина подчинена биномиальному закону
распределения, но при этом известно,
что “m”
– достаточно большое, а “p”
достаточная мала.
Равномерное
распределение для дискретных величин.
Если случайная величина Х принимает
конечное число значений с равными
вероятностями, то вероятность одного
(любого) события A
(х = m)
равна 1/n,
где n
– число опытов. Математическое ожидание:
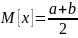 ,
где а – начальное возможное значение,
b
– конечное.
Дисперсия:
,
где а – начальное возможное значение,
b
– конечное.
Дисперсия:
 ;
Равномерное
распре-деление для непрерывных величин.
Говорят что случайная величина Х имеет
равномерное распределение если:
Х
может принимать любые значения на
интервале [a,
b];
в
каждой точке интервала [a,
b]
значение плотности распределения одно
и тоже. Плотность распределения: f(x)
=
;
Равномерное
распре-деление для непрерывных величин.
Говорят что случайная величина Х имеет
равномерное распределение если:
Х
может принимать любые значения на
интервале [a,
b];
в
каждой точке интервала [a,
b]
значение плотности распределения одно
и тоже. Плотность распределения: f(x)
=

Ф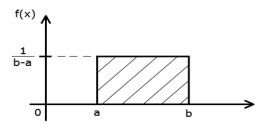 ункция
распределения:
F(x)
=
ункция
распределения:
F(x)
=
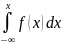 =
=

Мат.
ожидание:
M[x]
=
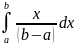 =
=
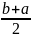 ;
Дисперсия:
D[x]
=
;
Дисперсия:
D[x]
=

