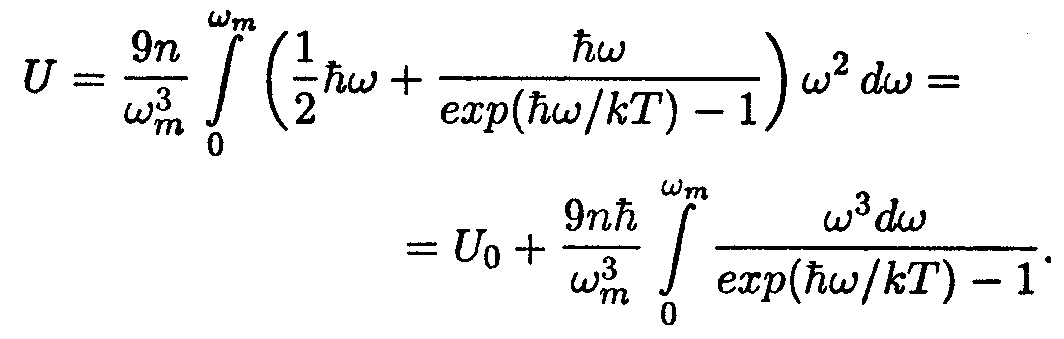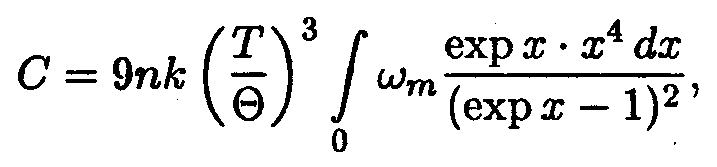1. Модель Эйнштейна

Эйнштейн отождествил кристаллическую решетку из N атомов с системой 3N независимых гармонических осцилляторов с одинаковой собственной частотой ω. Существование нулевой энергии колебаний было установлено значительно позже, лишь после создания квантовой механики. Поэтому Эйнштейн исходил из планковского значения энергии гармонического осциллятора ε_п = пћω. Соответственно в использованном Эйнштейном выражении для среднего значения энергии слагаемое ћω/2 отсутствовало.

Приняв, что распределение осцилляторов по состояниям с различной энергией

подчиняется закону Больцмана, можно найти среднее значение энергии гармонического осциллятора <ε>. Получается выражение, отличающееся от формулы Планка для средней энергии излучения лишь тем, что оно имеет дополнительное слагаемое ћω/2. Таким образом,

(1)

Умножив второе слагаемое выражения (1) на 3N, Эйнштейн получил для внутренней энергии кристалла формулу

(2)

Продифференцировав выражение (2) по температуре, Эйнштейн нашел теплоемкость кристалла:

(3)

Рассмотрим два предельных случая.

1. Высокие температуры (kТ >> ћω). В этом случае можно положить ехр(ћω /kТ) ≈ 1 + ћω /kТ в знаменателе и ехр(ћω /kТ) ≈ 1 — в числителе формулы . В результате для теплоемкости получается значение

C = 3NkТ.

Таким образом, мы пришли к закону Дюлонга и Пти.

2. Низкие температуры (kТ << ћω). При этом условии единицей в знаменателе выражения (3) можно пренебречь. Тогда формула для теплоемкости принимает вид

(4)

Экспоненциальный множитель изменяется значительно быстрее, чем Т ². Поэтому при приближении к абсолютному нулю выражение (4) будет стремиться к нулю практически по экспоненциальному закону.

Опыт показывает, что теплоемкость кристаллов изменяется вблизи абсолютного нуля не экспоненциально, а по закону Т ³. Следовательно, теория Эйнштейна дает лишь качественно правильный ход теплоемкости при низких температурах. Количественного согласия с опытом удалось достигнуть Дебаю.

2. Модель Дебая

В этой модели, как и в модели Эйнштейна, рассматривается изотропная среда, но учитывается дисперсия упругих волн.

Число стоячих волн, т. е. нормальных колебаний, частоты которых заключены в интервале от ω до ω + d ω, приходящихся на единицу объема V кристалла равно

(4)

где υ — фазовая скорость волны в кристалле. При выводе этой формулы предполагалось, что ω = υk, т.е. упругие волны имеют линейный закон дисперсии.

Формула (4) не учитывает возможных видов поляризации волны. В твердой среде вдоль некоторого направления могут распространяться три разные волны с одним и тем же значением ω, различающиеся направлением поляризации: одна продольная и две поперечные с взаимно перпендикулярными направлениями колебаний. В соответствии с этим формулу (4) нужно видоизменить следующим образом:

Здесь υ_||— фазовая скорость продольных, a υ_ — поперечных упругих волн. Положим для простоты, что υ_|| = υ_ = υ. Тогда

(5)

Максимальную частоту ω_т нормальных колебаний решетки можно найти, приравняв полное число колебаний числу степеней свободы, равному 3n (n — число атомов в единице объема кристалла; расчет производится для единицы объема):

Отсюда

(6)

В соответствии с(6) наименьшая длина волны, возбуждаемая в кристалле, оказывается равной

где d — расстояние между соседними атомами в решетке. Этот результат согласуется с тем, что волны, длина ко­торых меньше удвоенного межатомного расстояния, не имеют физического смысла.

Исключив из равенств (5) и (6) скорость υ, получим для числа нормальных колебаний dN_ω в интервале частот dω, приходящегося на единицу объема кристалла, следующее выражение

(7)

Внутренняя энергия единицы объема кристалла может быть представлена в виде

где <ε(ω)> — среднее значение энергии нормального колебания частоты ω. Подставив выражение (1) для <ε(ω)> и (7) для dN_ω придем к формуле

(8)

Здесь U₀ = Зп((3/8)ћω_m) — энергия нулевых колебаний кристалла.

Производная от U по Т дает теплоемкость единицы объема кристалла

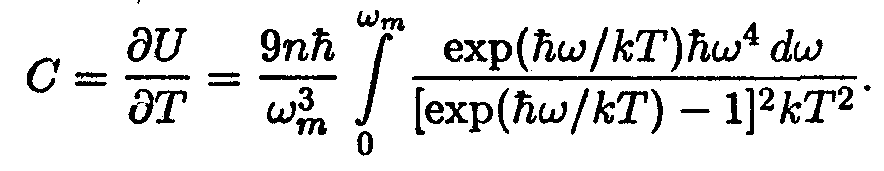
Величину Θ, определяемую условием

ћω_m = k Θ,

на­зывают характеристической температурой Дебая. Температура Дебая указывает для каждого вещества ту область, где становится существенным квантование энергии колебаний.

Введем переменную х = ћω/kТ. Тогда выражение для теплоемкости примет вид

(9)

где х_т = ћω_m/ kТ = Θ/Т. При Т << Θ верхний предел интеграла будет очень большим, так что его можно приближенно положить равным бесконечности (х_т ≈ ∞). Тогда интеграл будет представлять собой некоторое число, и теплоемкость С окажется пропорциональной кубу тем­пературы: С ~ T ³. Эта приближенная зависимость известна как закон Т ³ Дебая. При достаточно низких температурах этот закон выполняется во многих случаях очень хорошо.

При Т >> Θ, т. е. при ћω_m/ kТ << 1, формулу (8) можно упростить, положив ехр(ћω/kТ) ≈ 1 + ћω/kТ. То­гда для внутренней энергии получается выражение

а для теплоемкости — значение С = 3пk, фигурирующее в законе Дюлонга и Пти.

О 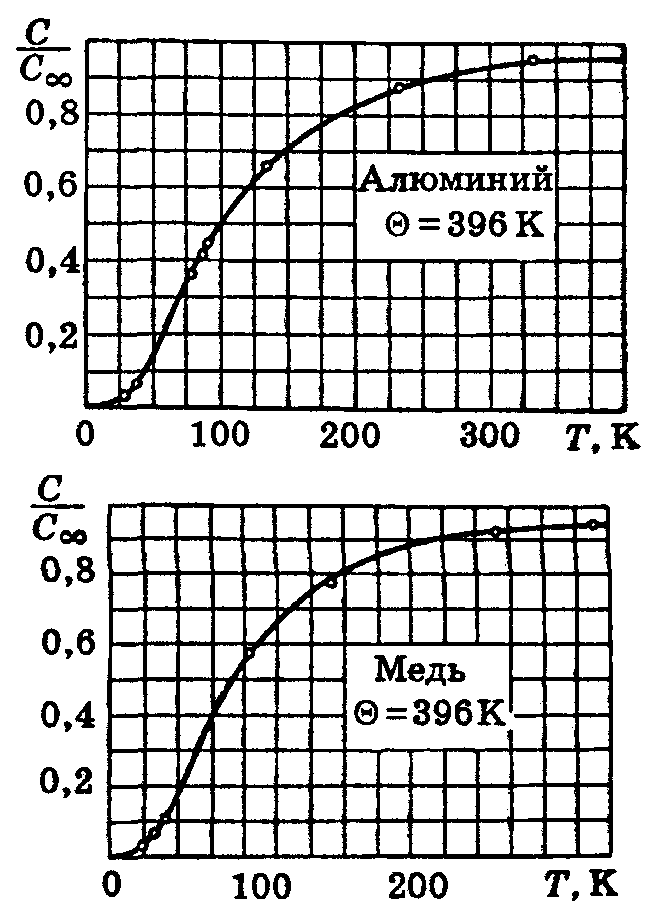согласии теории Дебая с опытом можно судить по рис. 1, на котором приведены данные для теплоемкости алюминия (Θ = 396 К) и меди (Θ = 309 К); С_∞ — классическое значение теплоемкости, получающееся из квантовых формул при Т → ∞. Кривые построены по формуле (9), кружками показаны экспериментальные точки.

Формула Дебая хорошо передает ход теплоемкости с температурой лишь для тел с простыми кристаллически­ми решетками, т. е. для химических элементов и некоторых

простых соединений.

Рис. 1

К телам с более сложной структурой формула Дебая неприменима. Это объясняется тем, что у таких тел спектр колебаний оказывается чрезвычайно сложным. В рассмотренном нами выше случае простой кристаллической решетки (у которой в элементарной ячейке содержится только один атом) каждому значению волнового вектора k соответствовали три значения собственной частоты колебаний решетки (одно для продольной и два значения для поперечных волн). Если число атомов в элементарной ячейке кристалла равно r, каждому значению k соответствует в общем случае 3r различных значений ω; следовательно, частота является много многозначной функцией волнового вектора, обладающей 3r ветвями. Так, например, в случае одномерной цепочки, построенной из чередующихся атомов двух сортов (r = 2), зависимость ω от k имеет вид, показанный на рис. 2. О 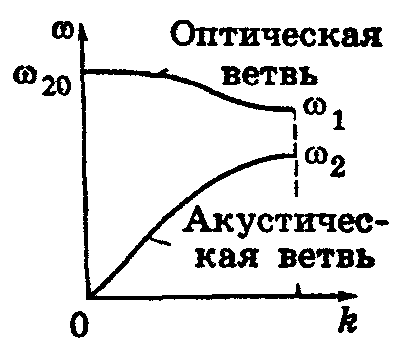дна из ветвей называется акустической, другая — оптической. Эти ветви различаются дисперсией, т. е. характером зависимости ω от k. Акустическая ветвь при убывании k идет в нуль, оптическая ветвь имеет своим пределом конечное значение ω_20.

В трехмерном случае из 3r ветвей три являются акустическими, остальные (3r - 3) — оптическими. Акустическим ветвям соответствуют звуковые частоты, оптическим — частоты, лежащие в инфракрасной области спектра. При нормальном колебании акустической частоты колеблются относительно друг друга аналогичные атомы, помещающиеся в различных элементарных ячейках. При нормальных колебаниях оптической частоты колеблются относительно друг друга различные атомы внутри каждой из элементарных ячеек; аналогичные атомы различных ячеек находятся при этом на неизменных расстояниях друг от друга.

Вывод: квантовая теория теплоемкости устанавливает прежде всего несправедливость теоремы о равномерном распределении энергии по степеням свободы в области низких и высоких температур; квантовая теория теплоемкости рассматривает колебания решетки как фононный газ; согласно квантовой теории теплоемкости, только при высоких температурах значения энергии и теплоемкости достигают величины, рассчитанной по кинетической теории газов.

ФОНОНЫ.

Фононы представляют собой кванты поля звуковых волн в макроскопическом теле. Теоретически они вводятся также как фотоны при квантовании электромагнитного поля. Электромагнитное поле может быть разложено в ряд Фурье по плоским волнам. При этом гамильтониан электромагнитного поля разлагается на сумму членов, каждый из которых эквивалентен гармоническому осциллятору. Квантами энергии этих гармонических осцилляторов и являются фотоны.

Аналогично гамильтониан твердого тела, которое построено из атомов, образующих кристаллическую решетку, может быть аппроксимирован суммой членов, каждый из которых представляет гармонический осциллятор, соответствующий нормальному колебанию системы атомов. В классической механике нормальное колебание есть волна деформации плоскостей решетки, т.е. звуковая волна. В квантовой механике такие колебания порождают кванты, называемые фононами.

Поэтому квантовое состояние кристаллической решетки, близкое к основному, должно характеризоваться числами имеющихся фононов с данными импульсами. Следовательно, при низких температурах твердое тело можно рассматривать как объем, содержащий газ невзаимодействующих фононов.

Поскольку фонон является квантом некоторого гармонического осциллятора, он имеет характеристическую частоту и энергию .

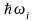Состояние решетки, характеризующееся наличием одного фонона, соответствует звуковой волне, записанной в виде: 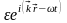, причем волновой вектор имеет величину , где с – скорость звука. Вектор поляризации 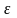не обязательно перпендикулярен волновому вектору . Таким образом, вектор поляризации имеет три независимые компоненты, соответствующие одному продольному колебанию – волне сжатия и двум поперечным колебаниям – волнам сдвига. Так как в возбужденном состоянии гармонический осциллятор может иметь любое число квантов, фононы подчиняются статистике Бозе, причем их полное число не сохраняется.

Твердое тело, состоящее из N атомов, имеет 3N нормальных колебаний, поэтому должно быть 3N различных типов фононов с характеристическими частотами

.

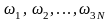Значения этих частот зависят от свойств решетки. В эйнштейновской модели решетки принимается, что все частоты равны между собой. Усовершенствованием этой модели является модель Дебая, который принял, что для определения частот, и только для этой цели, можно рассматривать твердое тело как упругий континуум объема V. Фононные частоты являются в этом случае 3N нижними нормальными частотами такой системы. Поскольку упругий континуум имеет непрерывное распределение частот, нас интересует число нормальных колебаний, частоты которых лежат между  и d. Чтобы найти это число, нужно учесть граничные условия для звуковой волны в упругой среде. Выбирая граничные условия периодичности, находим, как обычно,

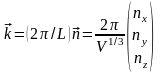, (1)

причем вектор 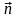имеет целые компоненты 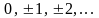.Интересующее нас число нормальных колебаний с частотами  и d равно

. (2)

Множитель 3 появляется из-за того, что возможны три направления поляризации. Поскольку 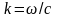, имеем

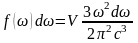. (3)

Максимальную частоту 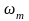определим из условия

, (4)

откуда при получим .

Длина волны, соответствующая , равна , т.е. примерно расстоянию между частицами.

Вычислим статистическую сумму для газа фононов. Энергия состояния, в котором имеется 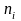фононов i-ого сорта, равна .

Фононы, так же как фотоны, подчиняются статистике Бозе. Ввиду отсутствия закона сохранения частиц, химический потенциал фононной системы равен нулю. Поэтому

(5)

Поскольку 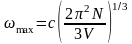, имеем:

, (6)

где 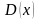- функция Дебая определяется следующим образом:

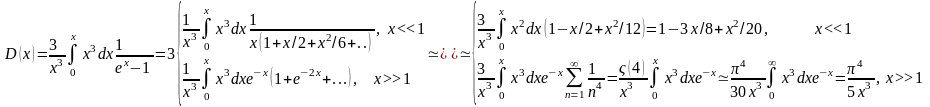, (3.64)

а 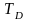-температура Дебая равна

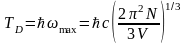. (7)

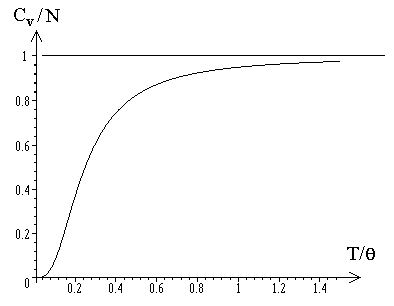
Рис.1.

Теплоемкость как функция температуры в модели Дебая.

Поэтому энергия имеет вид:

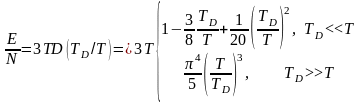. (8)

Соответственно, для теплоемкости получаем

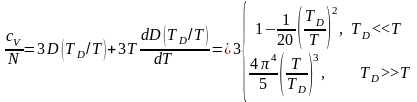. (9)

Фонон

(от греч. phone – звук) квант колебаний атомов кристаллической решетки. В кристаллических материалах атомы и молекулы активно взаимодействуют между собой, и рассматривать в них такие термодинамические явления, как колебания отдельных атомов, затруднительно — получаются огромные системы из триллионов связанных между собой линейных дифференциальных уравнений, аналитическое решение которых невозможно. Гораздо удобнее рассматривать согласованные колебания атомов кристалла как распространение в нем системы звуковых волн, квантами которых и являются фононы. Термин введен по аналогии с квантом электромагнитного поля - фотоном.Спин фонона равен нулю. Фонон принадлежит к числу бозонов и описывается статистикой Бозе-Эйнштейна. Понятие фонона позволяет описать тепловые и др. свойства кристаллов, используя методы кинетической теории газов. Фононы в большинстве случаев представляют собой главный тепловой резервуар твёрдого тела. Теплоёмкость кристаллического твёрдого тела практически совпадает с теплоёмкостью газа фононов. Теплопроводность кристалла можно описать как теплопроводность газа фононов. Рассеяние электронов проводимости при взаимодействии с фононами – основной механизм электросопротивления металлов и полупроводников. Способность электронов проводимости излучать и поглощать фононы приводит к притяжению электронов друг к другу, что при низких температурах является причиной перехода ряда металлов в сверхпроводящее состояние. Излучение фононов возбуждёнными атомами и молекулами тел обеспечивает возможность безызлучательных электронных переходов. В релаксационных процессах в твёрдых телах фононы обычно служат стоком для энергии, запасённой другими степенями свободы кристалла, например, электронными. Различают акустические и оптические фононы. Акустический фонон характеризуется при малых волновых векторах линейным законом дисперсии и параллельным смещением всех атомов в элементарной ячейке. Такой закон дисперсии описывает звуковые колебания решетки, поэтому фонон и называется акустическим .Оптические фононы существуют только в кристаллах, элементарная ячейка которых содержит два и более вида атомов. Эти фононы характеризуются при малых волновых векторах такими колебаниями атомов, при которых центр тяжести элементарной ячейки остается неподвижным. Энергия оптических фононов обычно достаточно велика (порядка 500 см-1) и слабо зависит от волнового вектора.