20. Энергия системы проводников с токами?????. Энергия магнитного поля. Объемная плотность энергии магнитного поля.

Проводник, c протекающим по нему электрическим током, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля. Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна Значит, энергия магнитного поля, которое связано с контуром, (1) Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем Так как I=Bl/(μ₀μN) и В=μ₀μH , то (2) где Sl = V — объем соленоида. Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью (3) Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н , т.е. оно относится только к пара- и диамагнетикам.

21. Вихревое электрическое поле. Первое уравнение Максвела в интегральной форме.

Возникновение индукционного тока в неподвижном проводнике при изменении магнитного потока свидетельствует о появлении в контуре сторонних сил, приводящих в движение заряды. Как мы уже знаем, эти сторонние силы обусловлены возникающим в контуре особым вихревым электрическим полем , циркуляция которого по замкнутому контуру отлична от нуля и равна ЭДС индукции:

.

С другой стороны, в соответствии с основным законом электромагнитной индукции Фарадея, величина ЭДС индукции определяется скоростью изменения потока магнитной индукции, то есть:

,

где интегрирование производится по произвольной поверхности, опирающейся на контур.

Приравнивая эти выражения, находим:

.

Максвелл предположил, что изменяющееся со временем магнитное поле приводит к появлению в пространстве электрического поля , независимо от того присутствует в этом пространстве проводящий контур или нет (рис.15.3). Наличие контура лишь позволяет обнаружить это электрическое поле по возникновению индукционного тока в проводнике.

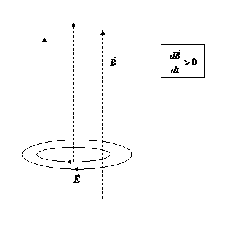
Рис.15.3. Вихревое электрическое поле.

В общем случае электрическое поле слагается из потенциального поля , циркуляция которого по замкнутому контуру равна нулю, и вихревого поля :

,

где

.

На основании сказанного, сложив циркуляции полей и , приходим к первому уравнению Максвелла в интегральной форме:

Интеграл в левой части берется по произвольному замкнутому контуру, в правой части – по произвольной поверхности, опирающейся на этот контур.