- •Контур с током в магнитном поле
- •Работа перемещения проводника и контура с током в магнитном поле
- •Действие магнитного поля на движущиеся электрические заряды. Сила Лоренца.
- •Движение заряженных частиц в магнитном поле. Принцип действия циклических ускорителей.
- •Эффект Холла.
- •Вихревой характер магнитного поля.
- •Закон полного тока. Применение закона полного тока для расчета магнитного поля тороида.
- •Магнитный поток. Теорема гаусса для магнитных полей.
- •Законы магнитных цепей
- •Магнетики. Намагничивание магнетиков. Вектор намагничения.
- •Напряженность магнитного поля. Связь между векторами j,b,h.
- •Доменная структура ферромагнетиков. Магнитный гистерезис.
- •Явление электромагнитной индукции. Закон Фарадея и правило Ленца.
- •Электронный механизм возникновения эдс индукции.
- •Явление самоиндукции. Индуктивность, единицы её измерения. Индуктивность длинного соленоида.
- •????? Установление тока в цепи, содержащей катушку индуктивности.
- •Взаимная индукция. Коэффициент взаимной индукции.
- •Энергия системы проводников с токами?????. Энергия магнитного поля. Объемная плотность энергии магнитного поля.
- •Вихревое электрическое поле. Первое уравнение Максвела в интегральной форме.
- •Взаимосвязь электрического и магнитного полей. Ток смещения. Второе уравнение теории максвелла в интегральной форме.
- •Полная система уравнений Максвелла в дифференциальной форме.
- •Природа носителей тока в металлах. Доказательство электронной проводимости металлов.
- •Классическая теория проводимости металлов. Вывод законов Ома и Джоуля-Ленца из электронной теории.
- •Связь между электропроводностью и теплопроводностью. Закон Видемана-Франца.
- •Трудности классической электронной теории.
- •Гармонические колебания. Линейный гармонический осциллятор. Математический и физический маятники.
- •Решения уравнения движения
- •Сложение гармонических колебаний.
- •Затухающие и вынужденные колебания.
- •Свободные колебания в электрическом колебательном контуре.
- •Вынужденные колебания. Добротность колебательного контура. Переменный электрический ток.
- •Резонанс напряжений в электрической цепи.
- •Резонанс токов в электрической цепи.
- •Автоколебания. Понятие о релаксационных колебаниях.
- •Упругие волны(продольные, поперечные). Уравнение бегущей волны(плоской сферической).
- •Уравнение плоской волны
- •Уравнение сферической волны
- •Свойства электромагнитных волн. Плоские электромагнитные волны.
- •Эффект Доплера для акустических и световых волн.?????
- •Энергия и импульс электромагнитных волн. Вектор Пойтинга.
- •Дипольное излучение электромагнитных волн.?????
- •Световые волны. Абсолютный и относительный показатели преломления. Интенсивность света.
- •Принцип Ферма. Вывод законов отражения и преломления света.
- •Когерентные волны. Способы получения когерентных волн.
- •Интерференция световых волн. Когерентность.
- •Расчет интерференционной картины от двух когерентных источников.
- •Интерференция в тонких пленках. Полосы равной толщины и равного наклона.
Действие магнитного поля на движущиеся электрические заряды. Сила Лоренца.
Сила Лоренца-сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.
![]()
где
q - заряд частицы;
V - скорость заряда;
B - индукции магнитного поля;
a -
угол между вектором скорости заряда и
вектором магнитной индукции.
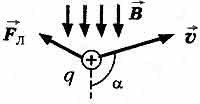
Направление силы Лоренца определяется по правилу левой руки:
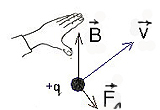
Если
поставить левую руку так, чтобы
перпендикулярная скорости составляющая
вектора индукции входила в ладонь, а
четыре пальца были бы расположены по
направлению скорости движения
положительного заряда (или против
направления скорости отрицательного
заряда), то отогнутый большой палец
укажет направление силы Лоренца
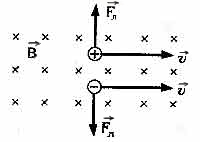
Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию). Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 и заряд в магнитном поле движется равномерно и прямолинейно. Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной
![]() и
создает центростремительное ускорение
равное
и
создает центростремительное ускорение
равное
![]()
В этом случае частица движется по окружности.
 Согласно
второму закону Ньютона: сила Лоренца
равнв произведению массы частицы на
центростремительное ускорение
Согласно
второму закону Ньютона: сила Лоренца
равнв произведению массы частицы на
центростремительное ускорение
![]() тогда
радиус окружности
тогда
радиус окружности
![]() а
период обращения заряда в магнитном
поле
а
период обращения заряда в магнитном
поле
![]()
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.
Движение заряженных частиц в магнитном поле. Принцип действия циклических ускорителей.
Формула
силы Лоренца дает возможность найти
ряд закономерностей движения заряженных
частиц в магнитном поле. Зная направление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле можно найти знак заряда
частиц, которые движутся в магнитных
полях.
Для вывода общих закономерностей
будем полагать, что магнитное поле
однородно и на частицы не действуют
электрические поля. Если заряженная
частица в магнитном поле движется со
скоростью v
вдоль линий магнитной индукции, то угол
α между векторами v
и В
равен 0 или π. Тогда сила Лоренца равна
нулю, т. е. магнитное поле на частицу не
действует и она движется равномерно и
прямолинейно.
В случае, если
заряженная частица движется в магнитном
поле со скоростью v,
которая перпендикулярна вектору В,
то сила Лоренца F=Q[vB]
постоянна по модулю и перпендикулярна
к траектории частицы. По второму закону
Ньютона, сила Лоренца создает
центростремительное ускорение. Значит,
что частица будет двигаться по окружности,
радиус r которой находится из условия
QvB=mv2/r
, следовательно
![]() (1)
Период
вращения частицы,
т. е. время Т, за которое она совершает
один полный оборот,
(1)
Период
вращения частицы,
т. е. время Т, за которое она совершает
один полный оборот,
![]() Подствавив
(1), получим
Подствавив
(1), получим
![]() (2)
(2)
т.
е. период вращения частицы в однородном
магнитном поле задается только величиной,
которая обратна удельному заряду (Q/m)
частицы, и магнитной индукцией поля, но
при этом не зависит от ее скорости (при
v<<c). На этом соображении основано
действие циклических ускорителей
заряженных частиц.
В случае, если
скорость v
заряженной частицы направлена под углом
α к вектору В
(рис. 170), то ее движение можно задать в
виде суперпозиции: 1) прямолинейного
равномерного движения вдоль поля со
скоростью vparall=vcosα
; 2) равномерного движения со скоростью
vperpend=vsinα
по окружности в плоскости, которая
перпендикулярна полю. Радиус окружности
задается формулой (1) (в этом случае надо
вместо v
подставить vperpend=vsinα).
В результате сложения двух данных
движений возникает движение по спирали,
ось которой параллельна магнитному
полю (рис. 1). Шаг винтовой (спиральной)
линии
![]() Подставив
в данное выражение (2), найдем
Подставив
в данное выражение (2), найдем
![]() Направление,
в котором закручивается спираль,
определяется знаком заряда частицы.
Если скорость v
заряженной частицы составляет угол α
с направлением вектора В
неоднородного
магнитного поля,
у которого индукция возрастает в
направлении движения частицы, то r и h
уменьшаются с увеличением В.
На этом основана фокусировка заряженных
частиц в магнитном поле.
Направление,
в котором закручивается спираль,
определяется знаком заряда частицы.
Если скорость v
заряженной частицы составляет угол α
с направлением вектора В
неоднородного
магнитного поля,
у которого индукция возрастает в
направлении движения частицы, то r и h
уменьшаются с увеличением В.
На этом основана фокусировка заряженных
частиц в магнитном поле.