- •Контур с током в магнитном поле
- •Работа перемещения проводника и контура с током в магнитном поле
- •Действие магнитного поля на движущиеся электрические заряды. Сила Лоренца.
- •Движение заряженных частиц в магнитном поле. Принцип действия циклических ускорителей.
- •Эффект Холла.
- •Вихревой характер магнитного поля.
- •Закон полного тока. Применение закона полного тока для расчета магнитного поля тороида.
- •Магнитный поток. Теорема гаусса для магнитных полей.
- •Законы магнитных цепей
- •Магнетики. Намагничивание магнетиков. Вектор намагничения.
- •Напряженность магнитного поля. Связь между векторами j,b,h.
- •Доменная структура ферромагнетиков. Магнитный гистерезис.
- •Явление электромагнитной индукции. Закон Фарадея и правило Ленца.
- •Электронный механизм возникновения эдс индукции.
- •Явление самоиндукции. Индуктивность, единицы её измерения. Индуктивность длинного соленоида.
- •????? Установление тока в цепи, содержащей катушку индуктивности.
- •Взаимная индукция. Коэффициент взаимной индукции.
- •Энергия системы проводников с токами?????. Энергия магнитного поля. Объемная плотность энергии магнитного поля.
- •Вихревое электрическое поле. Первое уравнение Максвела в интегральной форме.
- •Взаимосвязь электрического и магнитного полей. Ток смещения. Второе уравнение теории максвелла в интегральной форме.
- •Полная система уравнений Максвелла в дифференциальной форме.
- •Природа носителей тока в металлах. Доказательство электронной проводимости металлов.
- •Классическая теория проводимости металлов. Вывод законов Ома и Джоуля-Ленца из электронной теории.
- •Связь между электропроводностью и теплопроводностью. Закон Видемана-Франца.
- •Трудности классической электронной теории.
- •Гармонические колебания. Линейный гармонический осциллятор. Математический и физический маятники.
- •Решения уравнения движения
- •Сложение гармонических колебаний.
- •Затухающие и вынужденные колебания.
- •Свободные колебания в электрическом колебательном контуре.
- •Вынужденные колебания. Добротность колебательного контура. Переменный электрический ток.
- •Резонанс напряжений в электрической цепи.
- •Резонанс токов в электрической цепи.
- •Автоколебания. Понятие о релаксационных колебаниях.
- •Упругие волны(продольные, поперечные). Уравнение бегущей волны(плоской сферической).
- •Уравнение плоской волны
- •Уравнение сферической волны
- •Свойства электромагнитных волн. Плоские электромагнитные волны.
- •Эффект Доплера для акустических и световых волн.?????
- •Энергия и импульс электромагнитных волн. Вектор Пойтинга.
- •Дипольное излучение электромагнитных волн.?????
- •Световые волны. Абсолютный и относительный показатели преломления. Интенсивность света.
- •Принцип Ферма. Вывод законов отражения и преломления света.
- •Когерентные волны. Способы получения когерентных волн.
- •Интерференция световых волн. Когерентность.
- •Расчет интерференционной картины от двух когерентных источников.
- •Интерференция в тонких пленках. Полосы равной толщины и равного наклона.
ФИЗИКА
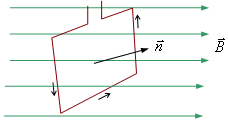
Контур с током в магнитном поле
Рис. 4.13 |
![]() .
.
Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке.
Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:
![]() .
.
Это выражение также можно использовать для определения индукции магнитного поля:
![]() .
.
Величину, равную
произведению
![]() ,
называют магнитным моментом контура
Рт.
Магнитный момент есть вектор, направление
которого совпадает с направлением
нормали к контуру. Тогда вращательный
момент можно записать
,
называют магнитным моментом контура
Рт.
Магнитный момент есть вектор, направление
которого совпадает с направлением
нормали к контуру. Тогда вращательный
момент можно записать
![]() .
.
При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.
Работа перемещения проводника и контура с током в магнитном поле
На
проводник с током в магнитном поле
действуют силы, которые определяются
с помощью закона Ампера. Если проводник
не закреплен (например, одна из сторон
контура сделана в виде подвижной
перемычки, рис. 1), то под действием силы
Ампера он в магнитном поле будет
перемещаться. Значит, магнитное поле
совершает работу по перемещению
проводника с током.
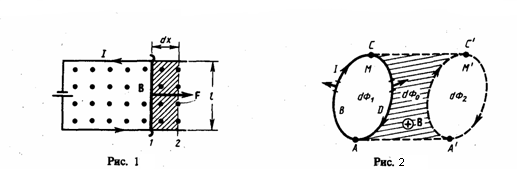 Для
вычисления этой работы рассмотрим
проводник длиной l
с током I (он может свободно двигаться),
который помещен в однородное внешнее
магнитное поле, которое перпендикулярно
плоскости контура. Сила, направление
которой определяется по правилу левой
руки, а значение — по закону Ампера,
рассчитывается по формуле
Для
вычисления этой работы рассмотрим
проводник длиной l
с током I (он может свободно двигаться),
который помещен в однородное внешнее
магнитное поле, которое перпендикулярно
плоскости контура. Сила, направление
которой определяется по правилу левой
руки, а значение — по закону Ампера,
рассчитывается по формуле
![]() Под
действием данной силы проводник
передвинется параллельно самому себе
на отрезок dx из положения 1 в положение
2. Работа, которая совершается магнитным
полем, равна
Под
действием данной силы проводник
передвинется параллельно самому себе
на отрезок dx из положения 1 в положение
2. Работа, которая совершается магнитным
полем, равна
![]() так
как ldx=dS
— площадь, которую пересекает проводник
при его перемещении в магнитном поле,
BdS=dФ — поток вектора магнитной индукции,
который пронизывает эту площадь. Значит,
так
как ldx=dS
— площадь, которую пересекает проводник
при его перемещении в магнитном поле,
BdS=dФ — поток вектора магнитной индукции,
который пронизывает эту площадь. Значит,
![]() (1)
т. е. работа по перемещению проводника
с током в магнитном поле равна произведению
силы тока на магнитный поток, пересеченный
движущимся проводником. Данная формула
справедлива и для произвольного
направления вектора В.
Рассчитаем работу по перемещению
замкнутого контура с постоянным током
I в магнитном поле. Будем считать, что
контур М перемещается в плоскости
чертежа и в результате бесконечно малого
перемещения перейдет в положение М',
изображенное на рис. 2 штриховой линией.
Направление тока в контуре (по часовой
стрелке) и магнитного поля (перпендикулярно
плоскости чертежа — за чертеж или от
нас) дано на рисунке. Контур М условно
разобьем на два соединенных своими
концами проводника: AВС и CDА.
Работа
dA, которая совершается силами Ампера
при иссследуемом перемещении контура
в магнитном поле, равна алгебраической
сумме работ по перемещению проводников
AВС (dA1)
и CDA (dA2),
т. е.
(1)
т. е. работа по перемещению проводника
с током в магнитном поле равна произведению
силы тока на магнитный поток, пересеченный
движущимся проводником. Данная формула
справедлива и для произвольного
направления вектора В.
Рассчитаем работу по перемещению
замкнутого контура с постоянным током
I в магнитном поле. Будем считать, что
контур М перемещается в плоскости
чертежа и в результате бесконечно малого
перемещения перейдет в положение М',
изображенное на рис. 2 штриховой линией.
Направление тока в контуре (по часовой
стрелке) и магнитного поля (перпендикулярно
плоскости чертежа — за чертеж или от
нас) дано на рисунке. Контур М условно
разобьем на два соединенных своими
концами проводника: AВС и CDА.
Работа
dA, которая совершается силами Ампера
при иссследуемом перемещении контура
в магнитном поле, равна алгебраической
сумме работ по перемещению проводников
AВС (dA1)
и CDA (dA2),
т. е.
![]() (2)
Силы, которые приложенны к участку
CDA контура, образуют острые углы с
направлением перемещения, поэтому
совершаемая ими работа dA2>0.
.Используя (1), находим, эта работа равна
произведению силы тока I в нашем контуре
на пересеченный проводником CDA магнитный
поток. Проводник CDA пересекает при своем
движении поток dФ0
сквозь поверхность, выполненную в цвете,
и поток dФ2,
который пронизывает контур в его конечном
положении. Значит,
(2)
Силы, которые приложенны к участку
CDA контура, образуют острые углы с
направлением перемещения, поэтому
совершаемая ими работа dA2>0.
.Используя (1), находим, эта работа равна
произведению силы тока I в нашем контуре
на пересеченный проводником CDA магнитный
поток. Проводник CDA пересекает при своем
движении поток dФ0
сквозь поверхность, выполненную в цвете,
и поток dФ2,
который пронизывает контур в его конечном
положении. Значит,
![]() (3)
Силы, которые действуют на участок
AВС контура, образуют тупые углы с
направлением перемещения, значит
совершаемая ими работа dA1<0.
Проводник AВС пересекает при своем
движении поток dФ0
сквозь поверхность, выполненную в цвете,
и поток dФ1, который пронизывает контур
в начальном положении. Значит,
(3)
Силы, которые действуют на участок
AВС контура, образуют тупые углы с
направлением перемещения, значит
совершаемая ими работа dA1<0.
Проводник AВС пересекает при своем
движении поток dФ0
сквозь поверхность, выполненную в цвете,
и поток dФ1, который пронизывает контур
в начальном положении. Значит,
![]() (4)
Подставляя (3) и (4) в (2), найдем выражение
для элементарной работы:
(4)
Подставляя (3) и (4) в (2), найдем выражение
для элементарной работы:
![]() где
dФ2—dФ1=dФ'
— изменение магнитного потока сквозь
площадь, которая ограничена контуром
с током. Таким образом,
где
dФ2—dФ1=dФ'
— изменение магнитного потока сквозь
площадь, которая ограничена контуром
с током. Таким образом,
![]() (5)
Проинтегрировав выражение (5), найдем
работу, которая совершается силами
Ампера, при конечном произвольном
перемещении контура в магнитном поле:
(5)
Проинтегрировав выражение (5), найдем
работу, которая совершается силами
Ампера, при конечном произвольном
перемещении контура в магнитном поле:
![]() (6)
значит, работа по перемещению
замкнутого контура с током в магнитном
поле равна произведению силы тока в
контуре на изменение магнитного потока,
сцепленного с контуром. Выражение (6)
верно для контура любой формы в
произвольном магнитном поле.
(6)
значит, работа по перемещению
замкнутого контура с током в магнитном
поле равна произведению силы тока в
контуре на изменение магнитного потока,
сцепленного с контуром. Выражение (6)
верно для контура любой формы в
произвольном магнитном поле.