18. Общее уравнение динамики
М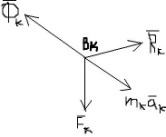
ех.сист.
дв-ся, на нее наложены идеал связи. Фк –
сумма всех актив сил,действ на т.Вк. Rк
– сумма всех реакций связи,действ на
т.Вк. Запишем основной з-н динамики для
т.Вк: mкaк=Fк+Rк
Fк+Rк
– mкaк=0
Fк+Rк+Фк=0
(все векторно) , т.е. точка формально
остановлена. Далее дадим этой формально
остан-й т. возм. перемещение △r
и подсчитаем сумму работ всех элемент.
сил, т.е. δr
(c
вектором) Fк
δr+Rк
δr+Фк
δr=0
δА(Fк)+δА(Rк)+
δА(Фк)=0 δА(Rк)=0
=> δА(Fк)+
δА(Фк)=0 (все вект) - общее ур-е динамики
Принцип Даламбера-Лагранжа (для точки).
Для системы точек: При дв-и мех.сист. с
идеал.связями в каждый момент времени
сумма элемент.работ активных сил и сил
инерции на любом возм.перем-и мех.сист.
=0. Смысл общего ур динамики заключ в
том,что его можно рассм как результат
послед-го применения 2х принципов –
сначала принципа Даламбера,затем
принципа возм переем-й. Это ур позволяет
решать все задачи Д,такие как сост-ть
ДУ дв-я сист, опред-ть силы,если известны
ускор-я, опред-ть a,
V
и переем-я если известны силы. Сост-ся
столько ур-й, сколько степеней свободы
имеет система.
19, Обобщенные координаты и скорости. Обобщенные силы. Обобщенные координаты- независящие друг от друга параметры с помощью которых можно определять положения положение всех тел механической системы в пространстве в любой момент времени.
Число степеней свободы равно числу обобщенных координат
X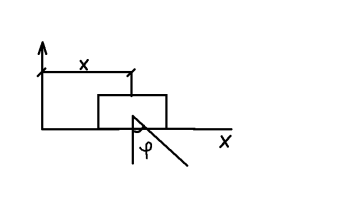
=q[м]
где q-
число обобщенных координат
2- обобщенные координаты
Даная система обладает 2-я степенями свободы. Обобщенные скорости:
Обощенные силы:
Обобщенная
сила 
соответствует обобщенной координате
,
есть скалярная величина заданных
активных сил равная сумме элементарных
работ на возможном перемещении 
Деленое
на 
Условие равновесия механической системы в обобщенных координатах
Для
равновесия механической системы
необходимо и достаточно, чтобы обощенная
сила механической системы равнялась
нулю 
(i=1…2…S) S-число уравнений (число степеней свободы)
20, Общее уравнение динамики в обобщенных силах. Ур-е Лагранжа 2 рода. Для равновесия механической системы необходимо и достаточно, чтобы каждая обобщ. Сила мех системы равнялась нулю.
Qi=0 i = 1,2,3….S ; S – число уравнений (ст. свободы). Уравнение Лагранжа 2го рода - метод решения задач динамики и прежде всего метод составления дифф-х уравнений движ-я мех. Системы, стеснённой голономными связями с помощью обобщ. координат.
d(δT/ δq1’) / dt - δT/ δq1= Q1;
…………………………………..
d(δT/ δqs’)/ dt - δT/ δqs = Qs
T – кинетическая энергия системы,
Замечания:
В этиз формулах кинет энеригя абсолютная, тоесть скорости абсолютные. Число ур-й Лагранжа = числу обобщ. коор-т. Ур-е Лагранжа позволяет решать все задачи динамики, в первую очередь составление дифф – х ур-й движения системы. Приращение обобщ-х корд-т следует направлять в сторону увеличения обоб-х коор-т.