2.9. Обобщенный метод наименьших квадратов

Проблемы автокорреляции и гетероскедастичности могут рассматриваться в рамках единого подхода, который часто называют обобщенным методом наименьших квадратов.

Пусть на основе n наблюдений рассматривается линейная модель множественной регрессии:

. (2.24)

Оба явления (автокорреляция и гетероскедастичность) находят свое отражение в структуре ковариационной матрицы случайных остатков:

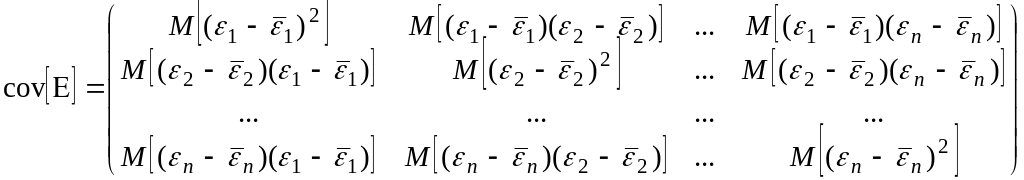
где символами (i=1,2,..,n) обозначены математические ожидания соответствующих случайных остатков: .

При выполнении условия ковариационная матрица записывается более компактно:

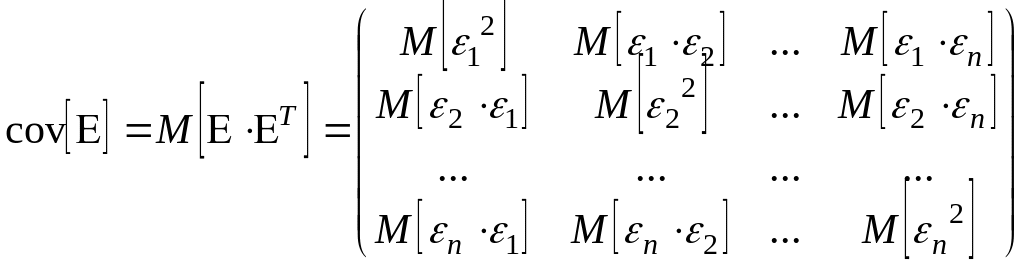. (2.25)

Для классической модели, для которой выполняются свойства гомоскедастичности ( ) и отсутствия автокорреляции ( при ij), ковариационная матрица имеет вид:

,

где I_n - единичная матрица размерности .

Исследуем модель (2.24) для общего случая ковариационной матрицы (2.25), которую запишем в виде:

, (2.26)

где - среднее значение дисперсий , i=1,2,…,n;

- симметричная матрица, вообще говоря, отличная от единичной.

Так в случае «чистой» гетероскедастичности матрица имеет вид:

,

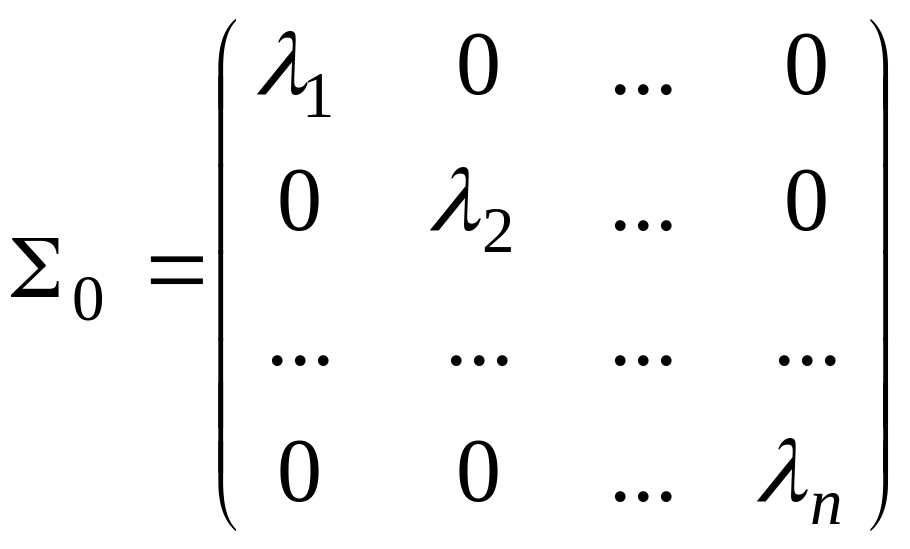а в случае автокорреляции первого порядка с некоторым параметром

.

Так как матрица является симметричной, то, согласно известному утверждению матричного исчисления, она может быть представлена в виде произведения некоторой матрицы С и матрицы С^Т , транспонированной к ней:

.

Умножая обе части этого тождества слева на C^-1 , а справа на (C^T)^-1, получим:

. (2.27)

Далее преобразуем исходную модель (2.24) умножением обеих частей слева на матрицу C^-1:

.

Введем в рассмотрение новые матричные переменные и , а также новую случайную компоненту . Тогда преобразованная модель имеет вид:

. (2.28)

Покажем, что полученная модель обладает свойствами гомоскедастичности и отсутствия автокорреляции. Другими словами, ковариационная матрица .

Действительно, используя (2.25), (2.26) и (2.27), а также известное матричное тождество (АВ)^Т=В^ТА^Т, получим

Итак, модель (2.28) является классической. Поэтому оценка ее параметров может быть произведена с помощью обычного МНК, т.е. имеет место равенство: . Учитывая представления переменных и , получим:

.

Но , следовательно, . Поэтому окончательно можем записать формулу оценки параметров на основе обобщенного метода наименьших квадратов:

(2.29)

Таким образом, знание матрицы , определяющей структуру взаимосвязи между случайными остатками и соответственно степень подверженности модели явлениям автокорреляции и гетероскедастичности, позволяет скорректировать оценки параметров регрессии в итоговой формуле.

2.10. Проблема мультиколлинеарности

Еще одной серьезной проблемой при построении моделей множественной регрессии является мультиколлинеарность – сильная линейная взаимосвязь двух или нескольких объясняющих переменных.

При наличии мультиколлинеарности параметры уравнения регрессии могут быть достаточно корректно определены с помощью МНК, и все уравнение может иметь достаточно высокие показатели качества (например, R²), но включение в модель мультиколлинеарных факторов нежелательно, поскольку:

• параметры имеют неправильные с точки зрения экономической теории знаки или неоправданно большие по абсолютной величине значения;

• оценки параметров становятся ненадежными, обнаруживают большие стандартные ошибки, т.е. не могут быть определены с достаточной точностью;

• оценки параметров оказываются очень чувствительными к небольшим изменениям в данных.

Указанные последствия мультиколлинеарности могут служить индикаторами ее наличия.

Тем не менее, если целью построения регрессии является прогнозирование результирующей переменной по известным значениям объясняющих переменных, то наличие мультиколлинеарности не приводит к смещению точечной прогнозной оценки.

Крайним случаем является полная мультиколлинеарность, которая предполагает строгую линейную зависимость между переменными. В этом случае матрица оказывается вырожденной, т.е. ее определитель равен нулю, что приводит к невозможности определения матрицы , с помощью которой вычисляют параметры уравнения регрессии. Полная мультиклоллинеарность встречается достаточно редко, поскольку ее можно достаточно просто избежать на этапе спецификации модели при отборе объясняющих переменных.

Для выявления частичной мультиколлинеарности в первую очередь анализируют матрицу K₀ парных коэффициентов корреляции объясняющих переменных:

.

Считается, что наличие значений коэффициентов корреляции, по абсолютной величине превосходящих 0,8, свидетельствует о присутствии мультиколлинеарности, хотя это не достаточно существенный признак. Оценка значимости мультиколлинеарности может быть проведена методом испытания гипотезы о независимости переменных [14].

Существование тесных линейных связей между объясняющими переменными приводит к тому, что определитель матрицы становится близким к нулю (сравнимым с ошибками вычислений), что может являться признаком мультиколлинеарности.

Самым простым способом преодоления мультиколлинеарности является исключение коллинеарных переменных из модели. При этом исключение переменных может происходить как на этапе множественного корреляционного анализа (см. параграф 2.2), так и апостериорным путем, т.е. после построения множественной регрессии. В последнем случае из модели исключается переменная, которой соответствует незначимый параметр с наименьшим абсолютным значением t-статистики. После чего строится новая регрессия с уменьшенным набором объясняющих переменных. Процесс продолжается до тех пор, пока все параметры модели не окажутся статистически значимыми.

При исключении из модели факторов происходит нарушение исходной спецификации и вкладываемого в нее смысла, а зачастую и интерпретации параметров. И если предположить, что исходная модель регрессии была истинной, оценки параметров, полученные после исключения факторов, будут смещенными. Поэтому переход к модели с меньшим числом влияющих переменных не всегда является эффективным.

Одним из способов преодоления мультиколлинеарности является переход к смещенным, но обладающим более высокой точностью, оценкам параметров уравнения регрессии. Одним из таких подходов является так называемая «ридж-регрессия». Он основан на вычислении несколько «подправленных» МНК-оценок следующего вида:

,

где  - небольшое положительное число.

Определитель матрицы уже будет отличен от нуля, хотя полученные оценки будут являться смещенными. Универсальных рекомендаций по выбору значения  не существует. Обычно его принимают в диапазоне от 0,1 до 0,4.