
- •1. Обработка информации и проблема интерпретации. Роль математического моделирования
- •Основные этапы математического моделирования
- •2. Основные понятия теории систем. Система и системное свойство
- •Понятия, характеризующие функционирование и развитие систем
- •Элемент
- •Подсистема
- •Структура
- •Состояние
- •Поведение
- •Модель функционирования (поведения) системы
- •3. Классификация систем
- •4. Взаимодействие системы с окружающей средой. Метаболизм
- •5. Определение понятия модели. Методы моделирования и классификация моделей
- •6. Математическая и компьютерная модель. Уровень идеализации и принцип минимальности
- •7. Цели моделирования и требования, предъявляемые к модели. Этапы компьютерного моделирования
- •8. Классификация математических и компьютерных моделей
- •Классификация км
- •9. Линейные модели и линейные системы уравнений. Проблемы вырождения и обусловленности
- •10. Интерполяция данных. Формулировка задачи интерполяции. Линейная интерполяция
- •Геометрическая интерпретация
- •11. Интерполяция полиномом и сплайны
- •Интерполяция многочленами
- •Метод решения задачи Полином Лагранжа
- •Полином Ньютона
- •Погрешность интерполирования
- •Выбор узлов интерполяции
- •12. Многомерная интерполяция данных
- •13. Идентификация моделей и задачи аппроксимации. Линейная аппроксимация и линеаризация
- •14. Нелинейная аппроксимация. Аппроксимация функцией произвольного вида. Аппроксимация полиномом
- •15. Нелинейная аппроксимация. Метод вложенных алгоритмов
- •16. Численное дифференцирование. Устойчивость и выбор шага дифференцирования
- •17. Вычисление определенных интегралов. Сравнительная характеристика методов Методы численного интегрирования
- •Интегрирование методом Монте-Карло
- •Обычный алгоритм Монте-Карло интегрирования
- •18. Метод Монте-Карло. Вычисление кратных интегралов
- •19. Моделирование стационарного состояния нелинейных систем
- •20. Моделирование динамики систем. Уравнения переходных процессов
- •Скалярное уравнение динамики системы
- •Векторное уравнение динамики системы
- •21. Моделирования динамики систем и численные методы решения задачи Коши
- •22. Жесткие системы. Неявные методы. Эквидистантный метод
- •23. Использование метода Монте-Карло при построении модели оптической пары "излучатель-приемник".
- •24. Стохастические модели. Получение случайных чисел с заданным распределением.
- •1.4. Моделирование случайных величин с заданным законом распределения
- •1. Метод нелинейного преобразования, обратного функции распределения
- •2. Метод Неймана
- •3. Метод кусочной аппроксимации
- •4. Некоторые специальные методы моделирования случайных величин
- •25. Модель источника случайных воздействий
- •26. Моделирование процессов кристаллизации. Расчет плоского кластера
- •27. Моделирование инерционных систем
- •28. Распределенные системы. Модель зонной печи
3. Метод кусочной аппроксимации
Существуют
различные приближенные приемы
моделирования случайных величин:
численное решение уравнения
![]() относительно
при
использовании метода нелинейного
преобразования, обратного функции
распределения; замена непрерывных
распределений соответствующими
дискретными распределениями, для которых
можно указать достаточно простые
моделирующие алгоритмы, и другие приемы
[10, 23]. Среди них универсальным и наиболее
простым является метод кусочной
аппроксимации, предложенный Н. П. Бусленко
[11].
относительно
при
использовании метода нелинейного
преобразования, обратного функции
распределения; замена непрерывных
распределений соответствующими
дискретными распределениями, для которых
можно указать достаточно простые
моделирующие алгоритмы, и другие приемы
[10, 23]. Среди них универсальным и наиболее
простым является метод кусочной
аппроксимации, предложенный Н. П. Бусленко
[11].
Сущность
этого метода состоит в следующем. Пусть
требуется получить случайную величину
с
функцией плотности
.
Предположим, что область возможных
значений величины
ограничена
интервалом
(неограниченное
распределение можно приближенно заменить
ограниченным). Разобьем интервал
на
![]() достаточно
малых интервалов
достаточно
малых интервалов
![]() ,
так, чтобы распределение заданной
случайной величины в пределах этих
интервалов можно было довольно точно
аппроксимировать каким-нибудь простым
распределением, например равномерным,
трапецеидальным и т. д. В дальнейшем
рассмотрим кусочную аппроксимацию
равномерным распределением (рис. 1.3).
,
так, чтобы распределение заданной
случайной величины в пределах этих
интервалов можно было довольно точно
аппроксимировать каким-нибудь простым
распределением, например равномерным,
трапецеидальным и т. д. В дальнейшем
рассмотрим кусочную аппроксимацию
равномерным распределением (рис. 1.3).
Пусть
![]() —
вероятность попадания случайной величины
в
каждый из интервалов
—
вероятность попадания случайной величины
в
каждый из интервалов
![]() .
Получать реализации величины
с
кусочно-равномерным распределением
можно, очевидно, в соответствии со
следующей схемой преобразования
случайных чисел: 1) случайным образом с
вероятностью
выбирается
интервал
;
2) формируется реализация
.
Получать реализации величины
с
кусочно-равномерным распределением
можно, очевидно, в соответствии со
следующей схемой преобразования
случайных чисел: 1) случайным образом с
вероятностью
выбирается
интервал
;
2) формируется реализация
![]() случайной
величины, равномерно распределенной в
интервале
случайной
величины, равномерно распределенной в
интервале
![]() ;
3) искомая реализация
;
3) искомая реализация
![]() получается
по формуле
получается
по формуле
![]() .
.
Случайный
выбор интервала
с
вероятностью
означает,
по существу, моделирование дискретной
случайной величины, принимающей
значений
![]() ,
с вероятностью
каждое,
что можно сделать достаточно просто
[11]. Интервал
,
с вероятностью
каждое,
что можно сделать достаточно просто
[11]. Интервал
![]() разбивается
на
интервалов
разбивается
на
интервалов
![]() длиной
длиной
![]() каждый.
Из датчика случайных равномерно
распределенных в интервале (0, 1) чисел
выбирается некоторая реализация
каждый.
Из датчика случайных равномерно
распределенных в интервале (0, 1) чисел
выбирается некоторая реализация
![]() .
Путем последовательного сравнения
с
.
Путем последовательного сравнения
с
![]() определяется
тот интервал
определяется
тот интервал
![]() ,
в котором оказывается
.
,
в котором оказывается
.
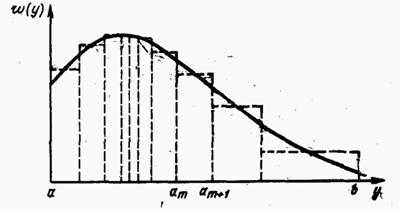
Рис. 1.3.
В основу этого процесса положен очевидный факт: вероятность попадания равномерно распределенной в интервале случайной величины в некоторый подинтервал равна длине этого подинтервала. Рассмотренный выше процесс представляет интерес не только как составной элемент метода кусочной аппроксимации, он широко используется в качестве алгоритма для моделирования дискретных случайных величин и случайных событий [10, 11].
Для
моделирования случайных величин методом
кусочной аппроксимации наиболее удобно
при машинной реализации выбирать
вероятности попадания во все интервалы
одинаковыми
![]() ,
а число
таким,
что
,
а число
таким,
что
![]() ,
где
,
где
![]() —
целое число, меньше или равное количеству
двоичных разрядов чисел, вырабатываемых
датчиком случайных чисел [10, 11]. В этом
случае величины
—
целое число, меньше или равное количеству
двоичных разрядов чисел, вырабатываемых
датчиком случайных чисел [10, 11]. В этом
случае величины
![]() должны
быть выбраны такими, чтобы
должны
быть выбраны такими, чтобы
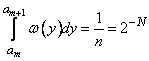 .
.
При
равенстве вероятностей
для
случайного выбора индекса
![]() можно
использовать первые
разрядов
числа, извлекаемого из датчика равномерно
распределенных случайных чисел.
можно
использовать первые
разрядов
числа, извлекаемого из датчика равномерно
распределенных случайных чисел.
Используя рассмотренный прием, приходим к следующему способу преобразования равномерно распределенных случайных чисел в случайные числа с заданным законом распределения.
Из
датчика равномерно распределенных в
интервале (0, 1) случайных чисел извлекается
пара реализаций
.
Первые
![]() разрядов
числа
разрядов
числа
![]() используются
для нахождения адресов ячеек, в которых
хранятся величины
и
используются
для нахождения адресов ячеек, в которых
хранятся величины
и
![]() ,
а затем по формуле
,
а затем по формуле
![]()
получается
реализация
случайной
величины
с
заданным законом распределения. Такой
алгоритм является довольно экономичным
по количеству требуемых операций,
которое не зависит от числа
,
т. е. не зависит от точности кусочной
аппроксимации. Однако с увеличением
точности аппроксимации возрастает
количество ячеек памяти, требуемое для
хранения величин
,
![]() ,
что является недостатком рассмотренного
метода, в особенности при больших
.
,
что является недостатком рассмотренного
метода, в особенности при больших
.
