Векторное уравнение динамики системы

Если векторными величинами являются как приращение динамического воздействия ΔU, так и приращение координаты состояния Δq, то векторными величинами являются и обе производные по времени от приращения координаты состояния: d(Δq)/dt и d²(Δq)/dt². К тому же, производная может быть записана, например, как в виде d(Δq)/dt, так и в виде dq/dt, так как функции q(t) и Δq(t) имеют одинаковый характер и отличаются только расположением начала координат на оси ординат, что более подробно пояснено на странице, посвяшенной приращению векторной величины. Но в уравнении динамики проще выглядит запись dq/dt. Поэтому, учтя это и все предыдущие замечания, уравнение динамики системы (3) следует записать в векторном виде для текущих значений динамического воздействия и координаты состояния ΔU_cv и Δq_cv так: a₀ Δq_cv + a₁ dq/dt + a₂ d²q/dt² + ... = − ΔU_cv , ( 4 ) Знак “−“ в правой части уравнения (4) появился потому, что вектор разности динамических воздействий ΔU противоположен по направлению вектору приращения координаты состояния Δq. Отметим также, что производные d(Δq)/dt и d²(Δq)/dt² имеют ненулевые значения только в период переходного процесса. В начале и по завершении переходного процесса (при переходе системы в новое равновесное состояние) они равны нулю, что позволяет определить конечное приращение координаты состояния Δq за конечный интервал времени Δt. Поэтому по завершении переходного процесса уравнение динамики превращается в уравнение: a₀ Δq = − ΔU , (5) где ΔU − разность начального и конечного значений динамического воздействия за весь период переходного процесса. В физике уравнением динамики часто называют второй закон Ньютона ma = F, где m – инертная масса. Однако второй закон Ньютона является частным случаем уравнения динамики (4) для механической прямолинейной формы движения, в которой a₀ = a₁ = 0, a₂ = m, Δq = Δх, а ΔU = − ΔF. Таким образом, второй закон Ньютона является уравнением динамики системы при пренебрежении влиянием трения и сжимаемостью тела. В форме записи ma = F он приемлем только при рассмотрении перемещения материальной точки, а это понятие, в принципе, является математической абстракцией. Обращаем особое внимание на то, что приращение динамического воздействия ΔU за промежуток времени Δt отличается от разности динамических воздействий U_Σ принципиально. Приращение динамического воздействия ΔU является разностью значений U в начальный и конечный моменты времени переходного процесса и применяется в уравнении динамики системы. А разность динамических воздействий U_Σ является разностью значений U на разных участках контрольной поверхности системы в один и тот же момент времени и применяется в уравнении состояния системы.

21. Моделирования динамики систем и численные методы решения задачи Коши

Постановка задачи Коши

Инженерные и научные задачи часто связаны с решением дифференциальных уравнений, так как с их помощью описываются многие физические явления. Для многих практически важных случаев задачи, описываемые дифференциальными уравнениями, весьма сложны, и получить их точное решение оказывается затруднительно или невозможно. Задачу Коши можно сформулировать следующим образом. Дано обыкновенное дифференциальное уравнение

(6.1)

и начальное условие

. (6.2)

Требуется найти функцию , удовлетворяющую уравнению (6.1) и начальному условию (6.2).

Методы решения задачи Коши делятся на одношаговые и многошаговые. К одношаговым относятся простой метод Эйлера, модифицированный метод Эйлера, метод Коши и метод Рунге–Кутта, к многошаговым – метод Адамса и предиктор-корректор метод (метод прогноза и коррекции).

Геометрически задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной. Заданием начального условия мы выделяем из семейства решений ту единственную кривую, которая проходит через фиксированную точку .

6.2. Метод Эйлера

Этот метод является простейшим численным методом решения задачи Коши. Рассмотрим его на примере решения обыкновенного дифференциального уравнения первого порядка (6.1) с соответствующим начальным условием (6.2).

Расчетную формулу метода Эйлера можно получить, используя разложение функции в ряд Тейлора в окрестности некоторой точки :

. (6.3)

Если приращение мало (то есть ), то членами ряда, начиная со слагаемого, включающего можно пренебречь, тогда

(6.4)

Воспользуемся формулой (6.4), применив ее к единственной известной из условия задачи точке . Найдем в производную , подставив (6.2) в (6.1):

.

Подставив последнее выражение в (6.4) и полагая , получим

или, сокращая обозначения, в окончательном виде

.

Таким образом, начальное условие (6.2) при известном значении функции в начальной точке позволяет найти приближенное значение при малом смещении от . На рис. 6.1 графически показан начальный шаг решения методом Эйлера.

Решение можно продолжить, используя найденное значение функции для вычисления следующего значения . Распространяя эти рассуждения на последующие точки, запишем расчетную формулу метода Эйлера в виде

(6.5)

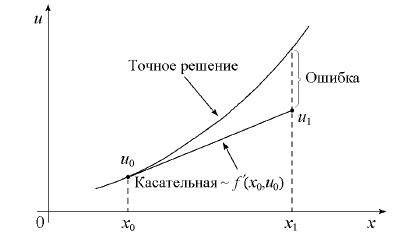
Рисунок 6.1 – Метод Эйлера

Из рисунка 6.1 видно, что ошибка метода Эйлера на шаге связана с используемой линейной аппроксимацией . Ошибка метода Эйлера на каждом шаге имеет порядок , так как члены, содержащие во второй и более высоких степенях, отбрасываются. Уменьшая можно снизить локальную ошибку на шаге.

Оценка погрешности метода Эйлера.

Локальной погрешностью метода называется величина . Найдем величину локальной погрешности метода Эйлера:

при условии, что . Другими словами - погрешность, которую допускает за один шаг метод, стартующий с точного решения. Глобальной погрешностью (или просто погрешностью) численного метода называют сеточную функцию со значениями в узлах. В качестве меры абсолютной погрешности метода примем величину . Можно показать, что для явных одношаговых методов из того, что локальная погрешность имеет вид следует, что , где С и M - некоторые константы. Таким образом, метод Эйлера является методом первого порядка точности. Для нахождения решения задачи Коши с заданной точностью требуется найти такое приближенное решение , для которого величина глобальной погрешности . Так как точное решение задачи неизвестно, погрешность оценивают с помощью правила Рунге.

Правило Рунге оценки погрешностей. Для практической оценки погрешности проводят вычисления с шагами h и h/2. За оценку погрешности решения, полученного с шагом h/2, принимают величину, равную 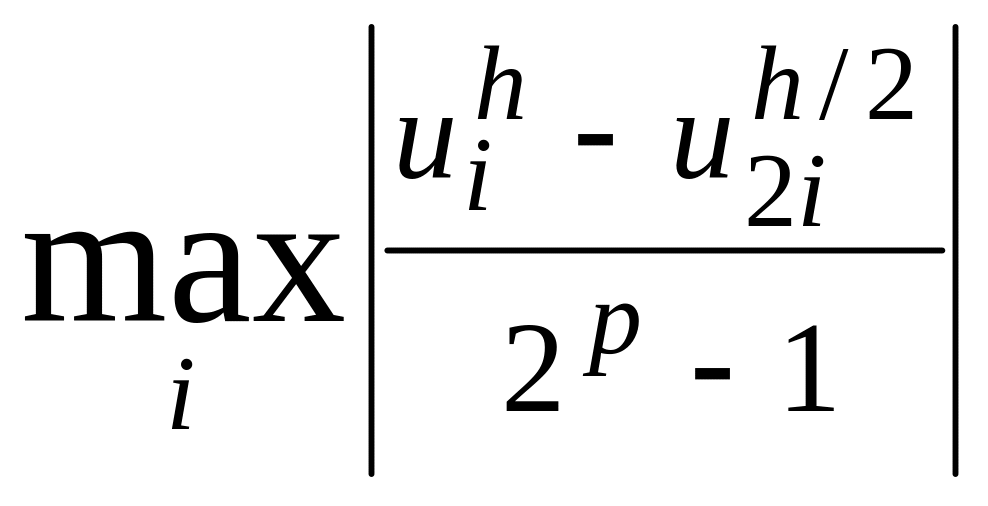, где p - порядок метода.

6.3. Модифицированный метод Эйлера

Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию на рассчитываемом шаге. Для этого при разложении в ряд Тейлора учтем дополнительно слагаемое, содержащее и в (6.3). Аппроксимируем вторую производную функции конечной разностью:

, (6.6)

где , и .

Подставляя полученное выражение в (6.3) и отбрасывая члены ряда, начиная со слагаемого, содержащего , запишем

.

Используя сокращенные обозначения, получим расчетную формулу модифицированного метода Эйлера

. (6.7)

Соотношение (6.7) дает решение для в неявном виде, поскольку присутствует одновременно в левой и правой его частях. Следует отметить, что неявные методы, как правило, более устойчивы, чем явные.

Формула (6.7) может рассматриваться и как явное решение, если в ее правую часть подставить значение , рассчитав его предварительно методом Эйлера по формуле (6.5). При этом значение является прогнозом, а уточнение результата по формуле (6.7) – его коррекцией. Непосредственная подстановка формулы Эйлера (6.5) в правую часть (6.7) дает расчетное соотношение метода Эйлера-Коши (или метода Хьюна). Графически модифицированный метод Эйлера представлен на рис. 6.2. Из рисунка 6.2 видно, что поправка, учитывающая изменение наклона кривой заметно уменьшает ошибку на шаге . Метод Эйлера называют методом ломаных, так как интегральная кривая на отрезке заменяется ломаной с угловым коэффициентом . В усовершенствованном методе Эйлера интегральная кривая на отрезке заменяется ломаной с угловым коэффициентом, вычисленным в средней точке отрезка. Так как значение в этой точке неизвестно, для его нахождения используют метод Эйлера с шагом .

Еще одна модификация метода Эйлера второго порядка - метод Эйлера-Коши:

Модифицированный метод Эйлера обеспечивает второй порядок точности. Ошибка на каждом шаге при использовании этого метода пропорциональна . Повышение точности достигается за счет дополнительных затрат машинного времени при расчете каждого шага.

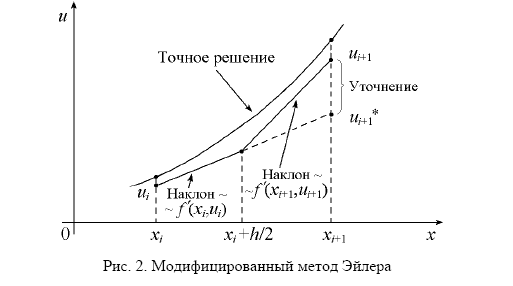
Рисунок 6.2 – Модифицированный метод Эйлера

6.4 Решение систем дифференциальных уравнений

Пусть требуется решить нормальную систему дифференциальных уравнений:

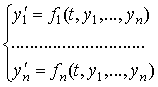
с начальными условиями:

Эту систему в векторной форме можно записать в виде:

, .

Здесь

, , .

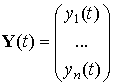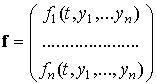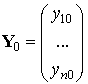Расчетная формула метода Эйлера имеет вид:

, .

6.5. Методы Рунге-Кутта

Дальнейшее снижение погрешности решения можно получить за счет использования лучшей аппроксимации , учитывающей слагаемые высоких порядков. Эта идея положена в основу методов Рунге-Кутта. Сущность построения группы методов Рунге-Кутта, заключается в аппроксимации решения дифференциального уравнения суммой

,

где – коэффициенты разложения, – последовательность функций

,

,

,

………………………………………,

.

где , , – некоторые параметры.

Одним из наиболее известных является вариант метода Рунге-Кутта, соответствующий . Это метод четвертого порядка точности, для которого ошибка на шаге имеет порядок . Его расчетные формулы имеют следующий вид:

, (6.8)

Где , ,

, .

Рассмотренные выше метод Эйлера и его модификация по сути дела являются методами Рунге-Кутта первого и второго порядка соответственно.

Один из методов третьего порядка выглядит так:

Где ,

,

,

Несмотря на увеличение объема вычислений метод четвертого порядка имеет преимущество перед методами первого и второго порядков, так как он обеспечивает малую локальную ошибку. Это позволяет увеличивать шаг интегрирования и, следовательно, сокращать время расчета.

6.6. Погрешность решения и выбор шага

Порядок точности метода определяет ошибку дискретизации . Знание порядка ошибки не обеспечивает ее прямую оценку. Получить такую оценку позволяет правило Рунге (формула двойного пересчета). Пусть одношаговый метод имеет порядок точности . Тогда погрешность, равная разности точного решения и приближенного , полученного численно с использованием шага , имеет порядок :

,

где – константа, не зависящая от . При расчете с уменьшенным вдвое шагом, равным , погрешность изменится:

.

Вычитая последнее выражение из предыдущего, определим изменение

.

Выражая из последнего соотношения постоянную и подставляя в предыдущую формулу, получим оценку погрешности по правилу Рунге:

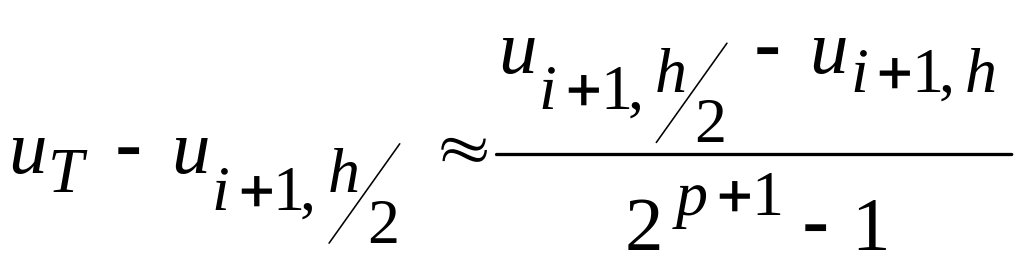. (6.9)

6.8. Многошаговые методы

Снижение погрешности решения задачи Коши может быть обеспечено использованием одношаговых методов высоких порядков точности. При этом в пределах каждого шага интегрирования приходится вводить промежуточные точки и увеличивать объем вычислений. Снизить вычислительные затраты без ухудшения погрешности можно, если на очередном шаге уточняющую информацию получать не за счет дополнительных точек, а из предыдущих шагов. Действительно, если в расчете использовать не только последнюю из известных точек решения, а еще и ряд предыдущих, можно более точно предсказать дальнейший ход кривой. Методы, реализующие эту идею, получили название многошаговых.

Простейшим многошаговым методом является двухшаговый метод Адамса.. Для получения расчетной формулы двухшагового метода проинтегрируем обе части дифференциального уравнения (6.1) на интервале от до .

Интегрирование левой части дает

. (6.10)

Для интегрирования правой части (6.1) заменим на интерполяционный многочлен . Для двух известных точек и может быть построен линейный многочлен, совпадающий с кривой решения в точках и :

Тогда интегрирование правой части дает

.

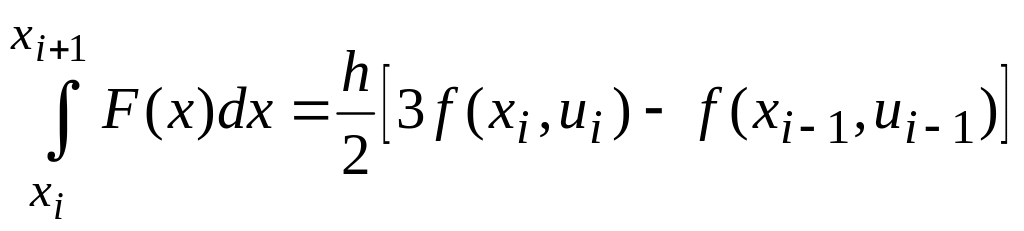Приравнивая правые части и применяя сокращенные обозначения , , запишем формулу двух шагового метода

.

Аналогично, учитывая большее число предыдущих точек решения можно построить формулы экстраполяционного метода Адамса-Башфорта:

;

.

Первая соответствует трех шаговому, а вторая – четырех шаговому методу.