1.4. Моделирование случайных величин с заданным законом распределения

Исходным материалом для формирования на ЦВМ случайных величин с различными законами распределения служат равномерно распределенные в интервале (0,1) случайные числа, которые вырабатываются на ЦВМ программным или же физическим датчиком случайных чисел.

Существуют различные приемы преобразования случайных чисел с равномерным распределением в случайные числа с заданным законом распределения [10, 23]. Так, например, в качестве нормально распределенных случайных чисел можно использовать сумму нескольких независимых случайных чисел с равномерным распределением (приближение основано на центральной предельной теореме теории вероятностей, в силу которой сумма независимых случайных величин при весьма общих условиях имеет асимптотически нормальное распределение).

Рассмотрим сначала общие приемы получения случайных чисел с заданным законом распределения из равномерно распределенных случайных чисел.

1. Метод нелинейного преобразования, обратного функции распределения

Пусть  — функция плотности,  – функция распределения вероятностей случайной величины , а  — функция, обратная функции . Тогда случайная величина  имеет заданный закон распределения , если случайная величина  равномерно распределена в интервале (0,1) [10].

Например, случайную величину с релеевским законом распределения, у которой функция плотности, функция распределения, среднее значение и дисперсия имеют соответственно вид

                          (1.4)

где  — параметр распределения, можно получить путем следующего преобразования равномерно распределенной в интервале (0,1) случайной величины :

(переход от  к  в последней формуле основан на том, что случайные величины  и  имеют здесь одинаковые законы распределения).

Аналогично случайную величину с показательным законом распределения, у которой

,             (1.5)

можно сформировать путем преобразования .

Путем преобразований

                       (1.6)

можно сформировать случайные числа, распределенные по закону арксинуса и закону Коши соответственно:

                     (1.7)

Используя свойство симметрии тригонометрических функций, нетрудно убедиться, что закон распределения случайных величин , формируемых согласно алгоритмам (1.6), не изменится, если аргумент  у тригонометрических функций заменить аргументом .

К сожалению, не всегда существуют элементарные преобразования для получения случайных величин с заданным законом распределения из равномерно распределенных случайных чисел. В частности, у случайных величин с нормальным распределением функция, обратная функции распределения, не выражается в замкнутом виде через элементарные функции. В этих случаях для формирования случайных величин с заданным распределением используются различные аппроксимации функции  [10, 23].

2. Метод Неймана

Для моделирования случайных величин, возможные значения которых не выходят за пределы некоторого ограниченного интервала  (случайные величины с усеченными законами распределения), а также случайных величин, законы распределения которых можно аппроксимировать усеченными, достаточно универсальным является метод Неймана [103], состоящий в следующем.

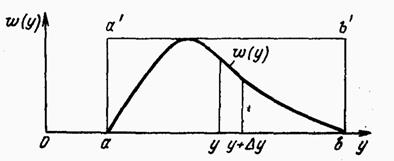
Рис. 1.2

Из датчика равномерно распределенных в интервале (0, 1) случайных чисел независимо выбираются пары чисел , из которых формируются преобразованные пары , ,  где  — интервал возможных значений случайной величины  с заданной функцией плотности ;  — максимальное значение функции . В качестве реализации случайной величины берется число  из тех пар ,  которых выполняется неравенство

.                                     (1.8)

Пары, не удовлетворяющие неравенству (1.8), выбрасываются.

Нетрудно убедиться в справедливости такого метода моделирования случайных величин. Действительно, пары случайных чисел ,  можно рассматривать как координаты случайных точек плоскости, равномерно распределенных вдоль осей  и  внутри прямоугольника  (рис. 1.2). Пары , , удовлетворяющие условию (1.8), — это координаты случайных точек плоскости, равномерно распределенных вдоль осей  и  внутри той части прямоугольника , которая расположена под кривой . Вероятность того, что случайная точка плоскости, находящаяся под кривой , окажется в элементарной полосе с основанием , очевидно, пропорциональна , а вероятность попадания точки под кривую  по условию равна единице, что и требуется.